问题说明:
假设数学表达式中允许包含两种括号:圆括号“()”和方括号“[]”,嵌套顺序任意。
正确的嵌套模式:( [ ] ( ) )、[ ( [ ] [ ] ) ]
正确的表达式例:(a+b)[c*(d-e)]
错误的嵌套模式:[ ( ] )、( ( ) ]
比如,在处理表达式(A)时
(A) 4+(2+8)*[5/(9-7)]
有以下步骤:
(1)检测到第一个括号“(”;
(2)检测到第二个括号“)”,说明子表达式 “4+(2+8)” 已完成匹配;
(3)检测到第三个括号“[”;
(4)检测到第四个括号“(”,与(3)中的括号不匹配,但由于同是左括号,可以继续匹配;
(5)检测到第五个括号“)”,由括号的作用可知,后来的括号比先来的括号优先级高,因此与(4)中括号匹配;
(6)检测到第六个括号“]”,由于原来优先级更高的括号已完成,因此与(3)中括号匹配。至此所有括号匹配完成。
解决方案:
可以看出,匹配成功的条件很简单:每一个检测到的括号与已检测到的优先级最高的括号都匹配。
匹配失败的条件:
(1)检测到与已检测到的优先级最高的括号不匹配的括号;
(2)扫描完整个表达式,还是有已检测到的括号没有完成匹配;
由于栈具有“先进后出”的特点,能很好地表现优先级这个性质,因此可以用栈来存储已经检测到的括号。
以(A)为例:



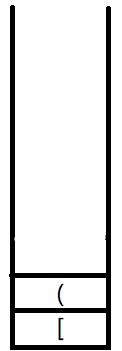



有以下步骤:
(1)检测到第一个括号“(”,进栈;
(2)检测到第二个括号“)”,进栈。子表达式 “4+(2+8)” 完成匹配,匹配的括号都出栈;
(3)检测到第三个括号“[”,进栈;
(4)检测到第四个括号“(”,进栈。与(3)中的括号不匹配,但由于同是左括号,可以继续匹配;
(5)检测到第五个括号“)”,进栈。由括号的作用可知,后来的括号比先来的括号优先级高,因此与(4)中括号匹配,匹配的括号都出栈;
(6)检测到第六个括号“]”,进栈。由于原来优先级更高的括号已完成,因此与(3)中括号匹配。匹配的括号都出栈,至此所有括号匹配完成。
需要注意的是,第一个括号进栈时,没有比较对象,因此需要特别处理。
判断函数 judge () 如下:
1 Status judge(Stack *S) 2 { 3 //进行表达式的输入和判断 4 SElemType *p; 5 char n; 6 7 scanf("%c",&n); //第一个括号的检测 8 while(n!='(' && n!='[') //忽略数字等其他符号,直到输入括号 9 { 10 if(n==')' || n==']' || n=='#') return FALSE; //若为')'或']',则表明不匹配。'#'用于结束输入 11 scanf("%c",&n); 12 } 13 14 if(n=='(' || n=='[') Push(S,n); //检测到左括号,进栈 15 scanf("%c",&n); 16 while(n!='#') //'#'用于结束输入 17 { 18 if(n=='(' || n==')' || n=='[' || n==']') 19 { 20 p=S->top; 21 Push(S,n); 22 if(*(p-1)=='(') //与前一个括号比较 23 { 24 if(*p==')') 25 { 26 printf("%c ",Pop(S)); 27 printf("%c ",Pop(S)); 28 } 29 else if(*p==']') return FALSE; 30 } 31 else if(*(p-1)=='[') 32 { 33 if(*p==']') 34 { 35 printf("%c ",Pop(S)); 36 printf("%c ",Pop(S)); 37 } 38 else if(*p==')') return FALSE; 39 } 40 } 41 scanf("%c",&n); 42 } 43 if(S->top==S->base) return TRUE; //栈内没有元素时,说明匹配 44 else return FALSE; 45 }
源代码如下:

#include <stdio.h> #include <stdlib.h> #define INIT_SIZE 10 #define INCREMENT 5 #define OVERFLOW -2 #define FALSE 0 #define OK 1 #define TRUE 1 #define ERROR 0 typedef char SElemType; typedef int Status; typedef struct stack{ SElemType *base; SElemType *top; int stacksize; }Stack; Status InitStack(Stack *S) { //初始化栈 S->base=(SElemType *)malloc(INIT_SIZE*sizeof(SElemType)); if(!S->base) exit(OVERFLOW); S->top=S->base; S->stacksize=INIT_SIZE; return OK; } Status Push(Stack *S,char e) { //入栈 if(S->top-S->base>=S->stacksize){ //栈满,重新分配内存 S->base=(SElemType *)realloc(S->base,(INIT_SIZE+INCREMENT)*sizeof(SElemType)); if(!S->base) exit(OVERFLOW); S->top=S->base+S->stacksize; S->stacksize+=INCREMENT; } *S->top++=e; return OK; } char Pop(Stack *S) { //出栈 char e; if(S->top==S->base) return ERROR; //栈空,出错 e=*(--S->top); return e; } Status judge(Stack *S) { //进行表达式的输入和判断 SElemType *p; char n; scanf("%c",&n); //第一个括号的检测 while(n!='(' && n!='[') //忽略数字等其他符号,直到输入括号 { if(n==')' || n==']' || n=='#') return FALSE; //若为')'或']',则表明不匹配。'#'用于结束输入 scanf("%c",&n); } if(n=='(' || n=='[') Push(S,n); //检测到左括号,进栈 scanf("%c",&n); while(n!='#') //'#'用于结束输入 { if(n=='(' || n==')' || n=='[' || n==']') { p=S->top; Push(S,n); if(*(p-1)=='(') //与前一个括号比较 { if(*p==')') { printf("%c ",Pop(S)); printf("%c ",Pop(S)); } else if(*p==']') return FALSE; } else if(*(p-1)=='[') { if(*p==']') { printf("%c ",Pop(S)); printf("%c ",Pop(S)); } else if(*p==')') return FALSE; } } scanf("%c",&n); } if(S->top==S->base) return TRUE; //栈内没有元素时,说明匹配 else return FALSE; } int main() { Stack Sta; Stack *S=&Sta; printf("INITIALIZING... "); if(InitStack(S)) printf("DONE! "); printf("enter an expression(stop by '#'): "); if(judge(S)==1) printf("It's True!"); else printf("It's False "); return 0; }
