缘来是区间重叠呀？

最近的一个活动配置需求，有一个非常奇葩的配置字段，可以配置活动在每天的某些时间段上线，如下图中“每日限时”，尽管已经是傻瓜操作了，但是考虑到严谨性，（实际上是为了防止产品手抖），如果两个时间段之间有重叠，应该合并两个时间段，比如下图两个时间段按道理应该合并成20:49~22:49。




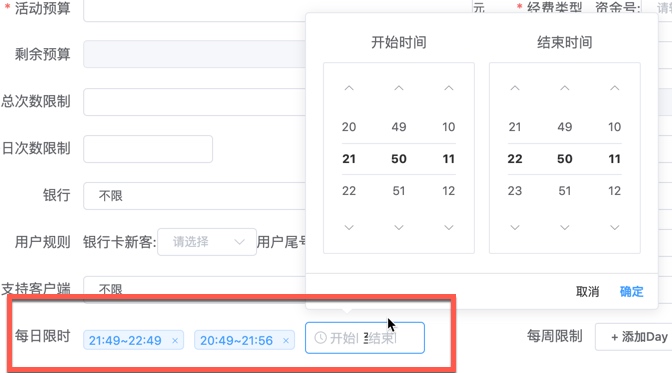
那么从代码层面该如何合并这两个时间段呢？首先需要判断两个时间段是否重叠，两个时间段如果有重叠的话，从正面考虑的话，它们的关系无外乎下面四种情况。


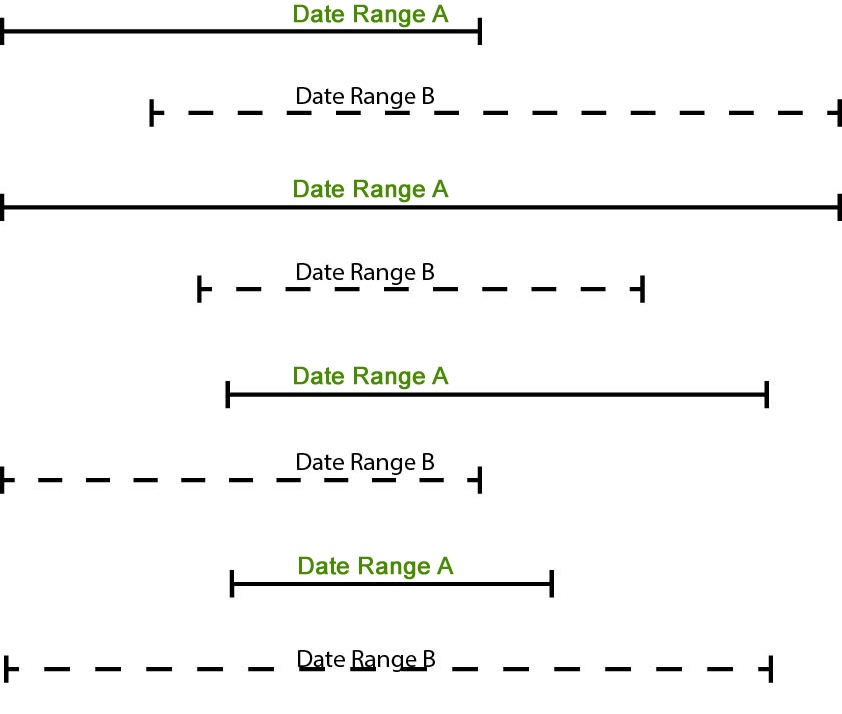
StartA <= EndB && StartB <= EndA
也就是说如果满足下述条件,则RangeA和RangeB有重叠

(StartA <= StartB && EndA >= StartB) || (StartB <= StartA && EndB >= StartA)

从反面考虑的话，似乎更容易理解，如下图，考虑时间段不重叠的情况。



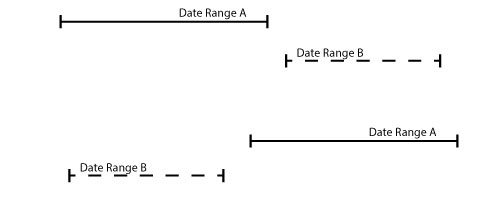
也就是说下面的条件下，两个时间不会发生重叠

EndA < StartB || StartA > EndB

对上面的条件取反就是两个时间段会重叠。根据摩根定律

!(EndA < StartB || StartA > EndB) = (EndA >= StartB) && (StartA <=EndB)

如果能判断出两个时间段有重叠部分，合并两个时间段非常简单：

Start = Max.min(StartA, StartB)
End = Max.max(EndA, EndB)

对于业务中遇到的时间段重叠问题，直接比较时间大小比较困难，只需要把所有时间转换成时间戳比较就简单的多了

StartA = new Date(StartA).getTime()

这样上述的比较问题就变成了整数之间的比较。类似的这种区间重叠问题是一个非常经典的问题，一看到这种模型，我就猜想LeetCode是否会有这种算法题。果不其然，我在LeetCode发现了完全一致的问题。解题思路很简单

Merge Intervals

Given a collection of intervals, merge all overlapping intervals.
Example 1:
Input: [[1,3],[2,6],[8,10],[15,18]]
Output: [[1,6],[8,10],[15,18]]
Explanation: Since intervals [1,3]and [2,6] overlaps, merge them into [1,6].

/**
 * @param {number[][]} intervals
 * @return {number[][]}
 */
var merge = function(intervals) {
  if (intervals.length < 2) {
    return intervals
  }
  // 先按照起始时间排序
  intervals.sort((v1, v2) => {
    return v1[0] - v2[0]
  })
  const result = []
  let [preStart, preEnd] = intervals[0]
  for (let len = intervals.length, i = 1; i < len; i++) {
    const [curStart, curEnd] = intervals[i]
    if (curStart <= preEnd) {
      // preEnd = Math.max(curEnd, preEnd)
      if (curEnd > preEnd) {
        preEnd = curEnd
      }
    } else {
      result.push([preStart, preEnd])
      preStart = curStart
      preEnd = curEnd
    }
  }
  result.push([preStart, preEnd])
  return result
}

另一个比较有趣的问题是，如果两个时间段有重叠部分，如何快速计算重叠部分的长度

前面我们提到了两个区段有重叠的四种情况，为了计算两个区段的重叠部分长度，最简单的方法是先判读两个区间段属于上图的哪一种情况，然后就很容易计算出来了,比如上面的四种情况对应的重叠部分分别是：EndA - StartB、EndB - StartB、EndB - StartA、EndA - StartA.而实际上并不需要区分上面的四种情况，上述四个计算式的最小值就能概括四种情况，即，如果两个区间段有重叠的话，其重叠部分的长度为

Math.min(EndA - StartB,EndB - StartB,EndB - StartA,EndA - StartA)

参考
Determine Whether Two Date Ranges Overlap