我们知道dijkstra可以求最短路,但是它还有一个更为强大的应用,dijkstra求次短路。
我们来看这强大的算法吧。
旅行
旅行团每天固定的从S城市出发到达T城市,为了省油要求尽量走最短路径或比最短路径长1单位距离的路径,求满足条件的路径条数。
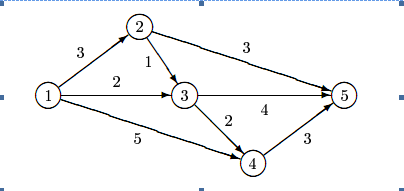
如上图:S=1,T=5,则有两条最短路,1->2->5和1->3->5 长度都为6,另外还有一条长度为7, 1->3->4->5
输入:
第一行一个数,表示数据的组数。
对于每组数据,第一行两个数,N和M,2 ≤ N ≤ 1, 000,1 ≤ M ≤ 10, 000,分别表示城市数和路的条数。
接下来M行,每行三个数A,B和L,1 ≤ A, B ≤ N,A <> B且 1 ≤ L ≤ 1, 000,表示有一条路从城市A到城市B,长度为L。道路是单向的,可能有多条路从A到B。
接下来一行,两个数S和T,1 ≤ S, F ≤ N,S<>T,表示起点城市和终点城市。
数据保证S和T间至少有一条路。
输出:
每组数据一个数,表示路径条数,答案不超过1 000 000 000.
样例:
Sample Input
2
5 8
1 2 3
1 3 2
1 4 5
2 3 1
2 5 3
3 4 2
3 5 4
4 5 3
1 5
5 6
2 3 1
3 2 1
3 1 10
4 5 2
5 2 7
5 2 7
4 1
Sample Output
3
2
说明:第一组数据对应上图。
20%的数据N<=10;
另有10%的数据N<=20;
另有10%的数据N<=30
这道题单从次短路角度思考,回忆最短路的做法,每次找出一个点,然后用这个边去松弛其他边,使所有非INF的点都满足在当前局面下的最优子结构这样一定可以找出答案。
那么怎么找出次短路呢,可以用相同的方法,每次找出一个最短路,用dz表示或一个最短路dc表示一个次短路。
这样,我们依然能保证这个点就是当前点的最短路或次短路(其中一个点的最短路一定优于次短路求出),那么得到这样一个之后,怎么更新呢。
Dijkstra的想法:记录最短路和次短路,每次用这个最短路和次短路更新周围的点。(这样做的想法是:次短路要么是u-v的次短路加上v到e的最短路,或者是到某个点的最短路加上次短路)
if一个最短路,那么他可以更新最短路和次短路,如果是是次短路,那么就可以更新次短路至于最短路,次短路计数,我认为,看了代码,你就会了。
#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int INF=0x3f3f3f3f; const int VM=1010; const int EM=10010; struct Edge{ int to,nxt; int cap; }edge[EM<<1]; int vis[VM][2],dis[VM][2]; // dis[i][0]:到点i的最短路 dis[i][1]:到点j的次短路 int head[VM],count[VM][2]; // count[i][0]:到点i的最短路的路数 len[i][1]:到点j的次短路的路数 int n,m,cnt; void addedge(int cu,int cv,int cw){ edge[cnt].to=cv; edge[cnt].cap=cw; edge[cnt].nxt=head[cu]; head[cu]=cnt++; } void Dijkstra(int src,int des){ memset(vis,0,sizeof(vis)); memset(count,0,sizeof(count)); int i=0; for(i=1;i<=n;i++){ dis[i][0]=INF; dis[i][1]=INF; } dis[src][0]=0; count[src][0]=1; int j,k,tmp,flag; for(i=1;i<=2*n-1;i++){ tmp=INF; // 找新的最短路和次短路 for(j=1;j<=n;j++) if(!vis[j][0] && tmp>dis[j][0]) { k=j; flag=0; tmp=dis[j][0]; } else if(!vis[j][1] && tmp>dis[j][1]) { k=j; flag=1; tmp=dis[j][1]; } if(tmp==INF) // 如果最短路和次短路都不存在,则退出for循环 break; vis[k][flag]=1; for(j=head[k];j!=-1;j=edge[j].nxt){ // 更新和点k相连的边 int v=edge[j].to; if(dis[v][0]>tmp+edge[j].cap){ // 比最短路短 dis[v][1]=dis[v][0]; count[v][1]=count[v][0]; dis[v][0]=tmp+edge[j].cap; count[v][0]=count[k][flag]; }else if(dis[v][0]==tmp+edge[j].cap){ // 等于最短路 count[v][0]+=count[k][flag]; }else if(dis[v][1]>tmp+edge[j].cap){ // 比次短路短 dis[v][1]=tmp+edge[j].cap; count[v][1]=count[k][flag]; }else if(dis[v][1]==tmp+edge[j].cap){ // 等于次短路 count[v][1]+=count[k][flag]; } } } if(dis[des][1]==dis[des][0]+1) count[des][0]+=count[des][1]; printf("%d ",count[des][0]); } int main(){ //freopen("input.txt","r",stdin); int t; scanf("%d",&t); while(t--){ cnt=0; memset(head,-1,sizeof(head)); scanf("%d%d",&n,&m); int u,v,w; while(m--){ scanf("%d%d%d",&u,&v,&w); addedge(u,v,w); } int src,des; scanf("%d%d",&src,&des); Dijkstra(src,des); } return 0; };
如果认为证明不够严密,那么点击这里