二叉树（二叉搜索树-AVL树-B树）

二叉树的概念：
　　度为2的树
二叉树的存储：
　　1、线性存储：适用于完全二叉树
　　2、链式存储：适用于所有二叉树
　　class BiTreeNode:
    　　def __init__(self, data):
        　　self.data = data
        　　self.lchild = None
        　　self.rchild = None

二叉树的遍历

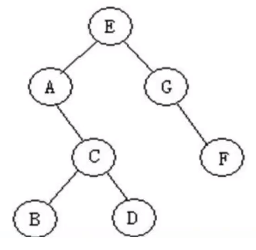
# 前序遍历：根节点最先遍历E,A,C,B,D,G,F --实现目录结构的显示
def pre_order(root):
    if root:
        print(root.data, end=',')
        pre_order(root.lchild)
        pre_order(root.rchild)

# 中序遍历：根节点在中间遍历A,B,C,D,E,G,F  --实现排序
def in_order(root):
    if root:
        in_order(root.lchild)
        print(root.data, end=',')
        in_order(root.rchild)

# 后序遍历：根节点在最后遍历B,D,C,A,F,G,E  --实现计算目录内文件size
def post_order(root):
    if root:
        post_order(root.lchild)
        post_order(root.rchild)
        print(root.data, end=',')

# 如果知道前、中、后序遍历的两种结果，可以还原树的结构
# 或者写函数还原树的结构

# 层次遍历：按层遍历，也适用于其他树。E,A,G,C,F,B,D  --实现计算迷宫路径最优解
from collections import deque
def level_order(root):
    queue = deque()
    queue.append(root)
    while len(queue) > 0:
        node = queue.popleft()
        print(node.data, end=',')
        if node.lchild:
            queue.append(node.lchild)
        if node.rchild:
            queue.append(node.rchild)

二叉搜索树：

如果一个二叉树满足，任意节点的所有左孩子(的key)都比这个节点(的key)小，
所有右孩子(的key)都比这个节点(的key)大，这个二叉树就是二叉搜索树

 

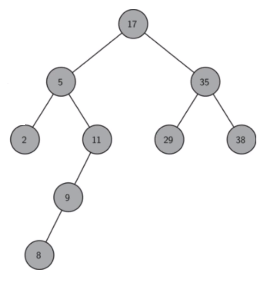
二叉搜索树的操作：查询、插入、删除
　　二叉搜索树的查询/插入操作最多只需要执行树的深度次，时间复杂度可以理解为O(log2n)

class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None
        self.rchild = None
        self.parent = None


class BinarySearchTree:
    def __init__(self, li=None):
        self.root = None
        if li:
            for val in li:
                self.insert(val)

    # def insert(self, node, val):  # 递归实现
    #     if not node:
    #         node = BiTreeNode(val)
    #     elif val < node.data:
    #         node.lchild = self.insert(node.lchild, val)
    #         node.lchild.parent = node
    #     elif val > node.data:
    #         node.rchild = self.insert(node.rchild, val)
    #         node.rchild.parent = node
    #     return node

    def insert(self, val):  # 非递归实现
        p = self.root
        if not p:
            self.root = BiTreeNode(val)
            return
        while True:
            if val < p.data:
                if p.lchild:
                    p = p.lchild
                else:
                    p.lchild = BiTreeNode(val)
                    p.lchild.parent = p
                    return
            elif val > p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = BiTreeNode(val)
                    p.rchild.parent = p
                    return
            else:
                return

    # def query(self, node, val):  # 递归
    #     if not node:
    #         return None
    #     if val > node.data:
    #         return self.query(node.rchild, val)
    #     elif node.data < val:
    #         return self.query(node.lchild, val)
    #     else:
    #         return node
    def query(self, val):  # 非递归
        p = self.root
        while p:
            if val < p.data:
                p = p.lchild
            elif val > p.data:
                p = p.rchild
            else:
                return p
        else:
            return None

    def __remove_case_1(self, node):
        '''
        情况1.如果要删除的节点是叶子节点：直接删除
        '''
        if not node.parent:
            self.root = None
        if node == node.parent.lchild:  # 是左孩子
            node.parent.lchild = None
        else:  # 是右孩子
            node.parent.rchild = None

    def __remove_case_21(self, node):
        '''
        情况2.如果要删除的节点只有一个孩子：将此节点的父亲与孩子连接，然后删除该节点
            2.1 如果要删除的节点只有一个左孩子
        '''
        if not node.parent:
            node.lchild.parent = None
            self.root = node.lchild
        elif node == node.parent.lchild:  # 要删除的节点是左孩子
            node.parent.lchild = node.lchild
            node.lchild.parent = node.parent
        else:  # 要删除的节点是右孩子
            node.parent.rchild = node.lchild
            node.lchild.parent = node.parent

    def __remove_case_22(self, node):
        '''
        情况2.如果要删除的节点只有一个孩子：将此节点的父亲与孩子连接，然后删除该节点
            2.2 如果要删除的节点只有一个右孩子
        '''
        if not node.parent:
            node.rchild.parent = None
            self.root = node.rchild
        elif node == node.parent.lchild:  # 要删除的节点是左孩子
            node.parent.lchild = node.rchild
            node.rchild.parent = node.parent
        else:  # 要删除的节点是右孩子
            node.parent.rchild = node.rchild
            node.rchild.parent = node.parent

    def delete(self, val):
        if self.root:
            node = self.query(val)
            if not node:
                return False
            if not node.lchild and not node.rchild:  # 1.叶子节点
                self.__remove_case_1(node)
            elif not node.rchild:  # 2.1只有一个左孩子
                self.__remove_case_21(node)
            elif not node.lchild:  # 2.2只有一个右孩子
                self.__remove_case_22(node)
            else:  # 3.如果要删除的节点有两个孩子：将其右子树的最小节点（该节点最多一个右孩子）删除，并替换当前节点。
                min_node = node.rchild
                while min_node.lchild:
                    min_node = min_node.lchild
                node.data = min_node.data
                if min_node.rchild:
                    self.__remove_case_22(min_node)
                else:
                    self.__remove_case_1(min_node)

    # 前序遍历
    def pre_order(self, root):
        if root:
            print(root.data, end=',')
            self.pre_order(root.lchild)
            self.pre_order(root.rchild)

    # 中序遍历：二叉搜索树的中序遍历是从小到大的排序
    def in_order(self, root):
        if root:
            self.in_order(root.lchild)
            print(root.data, end=',')
            self.in_order(root.rchild)

    # 后序遍历
    def post_order(self, root):
        if root:
            self.post_order(root.lchild)
            self.post_order(root.rchild)
            print(root.data, end=',')


b = BinarySearchTree([4, 3, 5, 6, 23, 7])
b.in_order(b.root)
print('
')
b.delete(5)
b.in_order(b.root)

二叉搜索树的遍历、查、增、删

AVL树：

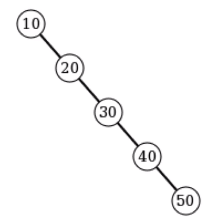
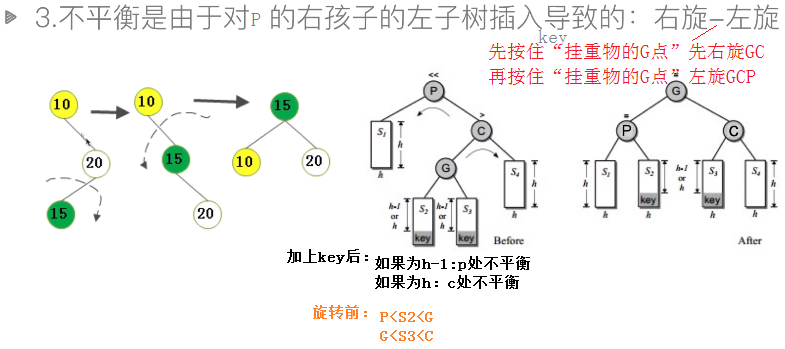
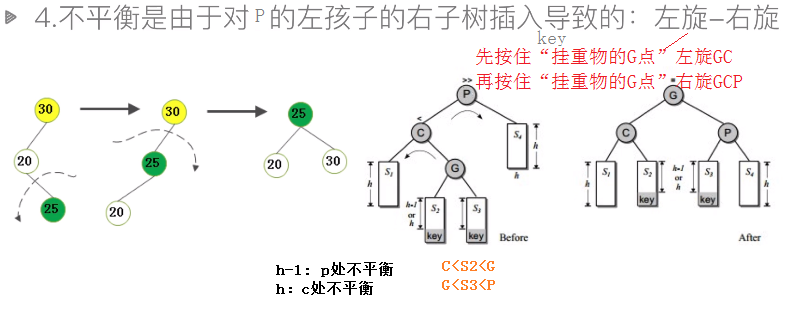
二叉搜索树在最坏情况下，搜索的时间复杂度为O(n)，见下图
解决方案是使用AVL树。

定义：任意节点的左右子树高度差不超过1，这样的树就是AVL树
balance factor用来表示每个节点的左右子树高度差

 

 

 

 

class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None
        self.rchild = None
        self.parent = None


class BinarySearchTree:
    def __init__(self, li=None):
        self.root = None
        if li:
            for val in li:
                self.insert(val)

    # def insert(self, node, val):  # 递归实现
    #     if not node:
    #         node = BiTreeNode(val)
    #     elif val < node.data:
    #         node.lchild = self.insert(node.lchild, val)
    #         node.lchild.parent = node
    #     elif val > node.data:
    #         node.rchild = self.insert(node.rchild, val)
    #         node.rchild.parent = node
    #     return node

    def insert(self, val):  # 非递归实现
        p = self.root
        if not p:
            self.root = BiTreeNode(val)
            return
        while True:
            if val < p.data:
                if p.lchild:
                    p = p.lchild
                else:
                    p.lchild = BiTreeNode(val)
                    p.lchild.parent = p
                    return
            elif val > p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = BiTreeNode(val)
                    p.rchild.parent = p
                    return
            else:
                return

    # def query(self, node, val):  # 递归
    #     if not node:
    #         return None
    #     if val > node.data:
    #         return self.query(node.rchild, val)
    #     elif node.data < val:
    #         return self.query(node.lchild, val)
    #     else:
    #         return node
    def query(self, val):  # 非递归
        p = self.root
        while p:
            if val < p.data:
                p = p.lchild
            elif val > p.data:
                p = p.rchild
            else:
                return p
        else:
            return None

    def __remove_case_1(self, node):
        '''
        情况1.如果要删除的节点是叶子节点：直接删除
        '''
        if not node.parent:
            self.root = None
        if node == node.parent.lchild:  # 是左孩子
            node.parent.lchild = None
        else:  # 是右孩子
            node.parent.rchild = None

    def __remove_case_21(self, node):
        '''
        情况2.如果要删除的节点只有一个孩子：将此节点的父亲与孩子连接，然后删除该节点
            2.1 如果要删除的节点只有一个左孩子
        '''
        if not node.parent:
            node.lchild.parent = None
            self.root = node.lchild
        elif node == node.parent.lchild:  # 要删除的节点是左孩子
            node.parent.lchild = node.lchild
            node.lchild.parent = node.parent
        else:  # 要删除的节点是右孩子
            node.parent.rchild = node.lchild
            node.lchild.parent = node.parent

    def __remove_case_22(self, node):
        '''
        情况2.如果要删除的节点只有一个孩子：将此节点的父亲与孩子连接，然后删除该节点
            2.2 如果要删除的节点只有一个右孩子
        '''
        if not node.parent:
            node.rchild.parent = None
            self.root = node.rchild
        elif node == node.parent.lchild:  # 要删除的节点是左孩子
            node.parent.lchild = node.rchild
            node.rchild.parent = node.parent
        else:  # 要删除的节点是右孩子
            node.parent.rchild = node.rchild
            node.rchild.parent = node.parent

    def delete(self, val):
        if self.root:
            node = self.query(val)
            if not node:
                return False
            if not node.lchild and not node.rchild:  # 1.叶子节点
                self.__remove_case_1(node)
            elif not node.rchild:  # 2.1只有一个左孩子
                self.__remove_case_21(node)
            elif not node.lchild:  # 2.2只有一个右孩子
                self.__remove_case_22(node)
            else:  # 3.如果要删除的节点有两个孩子：将其右子树的最小节点（该节点最多一个右孩子）删除，并替换当前节点。
                min_node = node.rchild
                while min_node.lchild:
                    min_node = min_node.lchild
                node.data = min_node.data
                if min_node.rchild:
                    self.__remove_case_22(min_node)
                else:
                    self.__remove_case_1(min_node)

    # 前序遍历
    def pre_order(self, root):
        if root:
            print(root.data, end=',')
            self.pre_order(root.lchild)
            self.pre_order(root.rchild)

    # 中序遍历：二叉搜索树的中序遍历是从小到大的排序
    def in_order(self, root):
        if root:
            self.in_order(root.lchild)
            print(root.data, end=',')
            self.in_order(root.rchild)

    # 后序遍历
    def post_order(self, root):
        if root:
            self.post_order(root.lchild)
            self.post_order(root.rchild)
            print(root.data, end=',')

 新增AVL树节点的逻辑：

令：右边高-> bf==1，左边高-> bf==-1
步骤1，先插入节点，插入方法跟二叉搜索树一样
步骤2，再更新节点的balance factor
从插入的节点一直更新到根，遇到0就跳出更新
插入的是左孩子，节点依次-1，直到根
　　-1后为0 ，跳出
　　-1后为-1，继续更新bf
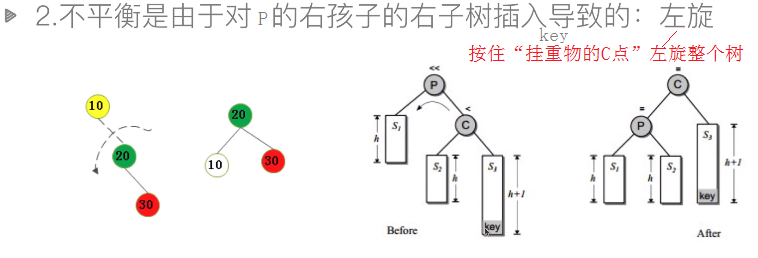
　　-1后为-2，旋转，在旋转函数里更新bf
插入的是右孩子，节点依次+1，直到根
　　+1后为0 ，跳出
　　+1后为1，继续更新bf
　　+1后为2，旋转，在旋转函数里更新bf
步骤3.把更新后的子树的根连接到原来的树上

class AVLNode(BiTreeNode):
    def __init__(self, data):
        BiTreeNode.__init__(self, data)
        self.bf = 0  # 节点的左右子树高度差


class AVLTree(BinarySearchTree):
    def __init__(self, li):
        BinarySearchTree.__init__(self, li)

    def rotate_left(self, p, c):
        # 左旋
        s2 = c.lchild
        p.rchild = s2
        if s2:
            s2.parent = p
        c.lchild = p
        p.parent = c

        p.bf = 0  # 没懂
        c.bf = 0  # 没懂
        # 返回新的根
        return c

    def rotate_right(self, p, c):
        # 右旋
        s2 = c.rchild
        p.lchild = s2
        if s2:
            s2.parent = p
        c.rchild = p
        p.parent = c

        p.bf = 0  # 没懂
        c.bf = 0  # 没懂

        return c

    def rotate_right_left(self, p, c):
        # 右旋
        g = c.lchild
        s3 = g.rchild
        c.lchild = s3
        if s3:
            s3.parent = c
        g.rchild = c
        c.parent = g
        # 左旋
        s2 = g.lchild
        p.rchild = s2
        if s2:
            s2.parent = p
        g.lchild = p
        p.parent = g

        # 更新节点平衡度
        if g.bf > 0:
            p.bf = -1
            c.bf = 0
        elif g.bf < 0:
            p.bf = 0
            c.bf = 1
        else:  # 插入的是g
            p.bf = 0
            c.bf = 0
        return g

    def rotate_left_right(self, p, c):
        g = c.rchild
        s2 = g.lchild
        c.rchild = s2
        if s2:
            s2.parent = c
        g.lchild = c
        c.parent = g

        s3 = g.rchild
        p.lchild = s3
        if s3:
            s3.parent = p
        g.rchild = p
        p.parent = g

        # 更新节点平衡度
        if g.bf < 0:
            p.bf = 1
            c.bf = 0
        elif g.bf > 0:
            p.bf = 0
            c.bf = -1
        else:  # 插入的是g
            p.bf = 0
            c.bf = 0
        return g

    def insert(self, val):
        # 1.和BST一样，插入节点
        p = self.root
        if not p:  # 空树
            self.root = AVLNode(val)
            return
        while True:
            if val < p.data:
                if p.lchild:
                    p = p.lchild
                else:
                    p.lchild = AVLNode(val)
                    p.lchild.parent = p
                    node = p.lchild
                    break
            elif val > p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = AVLNode(val)
                    p.rchild.parent = p
                    node = p.rchild
                    break
            else:
                return
        # 2.更新balance factor
        while node.parent:  # 是否为根节点，到根节点才停止
            if node.parent.lchild == node:  # 传递是从左子树来的，左子树更沉

                # 更新node.parent.bf -= 1
                if node.parent.bf < 0:  # 原来的bf == -1
                    g = node.parent.parent  # 为了连接旋转之后的子树
                    x = node.parent  # 保存旋转前的子树的根
                    if node.bf > 0:  # 判断是左旋还是左旋右旋
                        n = self.rotate_left_right(node.parent, node)
                    else:
                        n = self.rotate_right(node.parent, node)
                elif node.parent.bf > 0:
                    node.parent.bf = 0
                    break
                else:
                    node.parent.bf = -1
                    node = node.parent
                    continue
            else:  # 传递是从右子树来的，右子树更沉
                # 更新node.parent.bf += 1
                if node.parent.bf > 0: # 更新后变成2了，需要旋转
                    g = node.parent.parent  # 为了连接旋转之后的子树
                    x = node.parent  # 保存旋转前树的根
                    # 判断是右旋还是右旋左旋
                    if node.bf < 0:
                        n = self.rotate_right_left(node.parent, node)
                    else:
                        n = self.rotate_left(node.parent, node)
                elif node.parent.bf < 0: # 原来为-1更新后变成0，不再向上传递
                    node.parent.bf = 0
                    break
                else:  # 原来为0，更新后变为1
                    node.parent.bf = 1
                    node = node.parent
                    continue
            # 连接
            n.parent = g
            if g:
                if x == g.lchild:
                    g.lchild = n
                else:
                    g.rchild = n
                break
            else:
                self.root = n
                break

tree = AVLTree([9,8,7,6,5,4,3,2,1])
tree.pre_order(tree.root)
print('')
tree.in_order(tree.root)
print('')
tree.post_order(tree.root)

23423