Educational Codeforces Round 86 (Rated for Div. 2)

A. Road To Zero

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given two integers xx and yy. You can perform two types of operations:

1. Pay aa dollars and increase or decrease any of these integers by 11. For example, if x=0x=0 and y=7y=7 there are four possible outcomes after this operation:
   • x=0x=0, y=6y=6;
   • x=0x=0, y=8y=8;
   • x=−1x=−1, y=7y=7;
   • x=1x=1, y=7y=7.
2. Pay bb dollars and increase or decrease both integers by 11. For example, if x=0x=0 and y=7y=7 there are two possible outcomes after this operation:
   • x=−1x=−1, y=6y=6;
   • x=1x=1, y=8y=8.

Your goal is to make both given integers equal zero simultaneously, i.e. x=y=0x=y=0. There are no other requirements. In particular, it is possible to move from x=1x=1, y=0y=0 to x=y=0x=y=0.

Calculate the minimum amount of dollars you have to spend on it.

Input

The first line contains one integer tt (1≤t≤1001≤t≤100) — the number of testcases.

The first line of each test case contains two integers xx and yy (0≤x,y≤1090≤x,y≤109).

The second line of each test case contains two integers aa and bb (1≤a,b≤1091≤a,b≤109).

Output

For each test case print one integer — the minimum amount of dollars you have to spend.

判断一下就行，两种情况：一个是先把较大的数调成较小的数，然后在一块减去，或者各自减各自的，比较一下大小。

#include<iostream>
typedef long long ll;
using namespace std;
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        ll x,y;
        ll a,b;
        cin>>x>>y;
        cin>>a>>b;
        if(x==0&&y==0)
        {
            cout<<"0"<<endl;
        }
        else
        {
            ll sum1=0;
            ll sum2=0;
            if(x>=y){
                ll s=x-y;
                sum1=s*a;
                sum1+=(y*b);
                sum2=x*a+y*a;
                cout<<min(sum2,sum1)<<endl;
            }
            if(x<y)
            {
                ll s=y-x;
                sum1=s*a;
                sum1+=(x*b);
                sum2=a*x+a*y;
                cout<<min(sum1,sum2)<<endl;
            }
        }
    }

}

B. Binary Period

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Let's say string ss has period kk if si=si+ksi=si+k for all ii from 11 to |s|−k|s|−k (|s||s| means length of string ss) and kk is the minimum positive integer with this property.

Some examples of a period: for ss="0101" the period is k=2k=2, for ss="0000" the period is k=1k=1, for ss="010" the period is k=2k=2, for ss="0011" the period is k=4k=4.

You are given string tt consisting only of 0's and 1's and you need to find such string ss that:

1. String ss consists only of 0's and 1's;
2. The length of ss doesn't exceed 2⋅|t|2⋅|t|;
3. String tt is a subsequence of string ss;
4. String ss has smallest possible period among all strings that meet conditions 1—3.

Let us recall that tt is a subsequence of ss if tt can be derived from ss by deleting zero or more elements (any) without changing the order of the remaining elements. For example, tt="011" is a subsequence of ss="10101".

Input

The first line contains single integer TT (1≤T≤1001≤T≤100) — the number of test cases.

Next TT lines contain test cases — one per line. Each line contains string tt (1≤|t|≤1001≤|t|≤100) consisting only of 0's and 1's.

Output

Print one string for each test case — string ss you needed to find. If there are multiple solutions print any one of them.

判断t中是否同时有0、1.

如果单一，最小周期为1：直接输出

如果同时有0，1，最小周期为2：输出01间隔串还要注意t是s的子串，不是s是t的子串（就因为这个在哪傻逼了半天。。。。）

#include<iostream>
typedef long long ll;
#include<map>
using namespace std;
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        map<char,int>q;
        string s;
        cin>>s;
        int l=s.size();
        int ans1=0;
        int ans2=0;
        for(int i=0;i<l;i++)
        {
           if(s[i]=='1')
            ans1++;
           else
            ans2++;
        }
        if(ans1==0||ans2==0)
            cout<<s;
        else
        {
            for(int i=0;i<l;i++)
                cout<<"01";
        }
        cout<<endl;
    }

}

C. Yet Another Counting Problem

time limit per test

3.5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given two integers aa and bb, and qq queries. The ii-th query consists of two numbers lili and riri, and the answer to it is the number of integers xx such that li≤x≤rili≤x≤ri, and ((xmoda)modb)≠((xmodb)moda)((xmoda)modb)≠((xmodb)moda). Calculate the answer for each query.

Recall that ymodzymodz is the remainder of the division of yy by zz. For example, 5mod3=25mod3=2, 7mod8=77mod8=7, 9mod4=19mod4=1, 9mod9=09mod9=0.

Input

The first line contains one integer tt (1≤t≤1001≤t≤100) — the number of test cases. Then the test cases follow.

The first line of each test case contains three integers aa, bb and qq (1≤a,b≤2001≤a,b≤200; 1≤q≤5001≤q≤500).

Then qq lines follow, each containing two integers lili and riri (1≤li≤ri≤10181≤li≤ri≤1018) for the corresponding query.

Output

For each test case, print qq integers — the answers to the queries of this test case in the order they appear.计算[0,ab)[0,ab)区间内满足数量

思路 ：打表找规律，具有周期性a*b。

计算[1,ab]区间内满足数量，先处理好一个区间的，然后，后面的进项构造就行了。

前缀和处理好，然后( r/n - (l-1)/n )*num[n] + num[r%n] - num[(l-1)%n]。

解释一下：( r/n - (l-1)/n )*num[n] + num[r%n] - num[(l-1)%n].

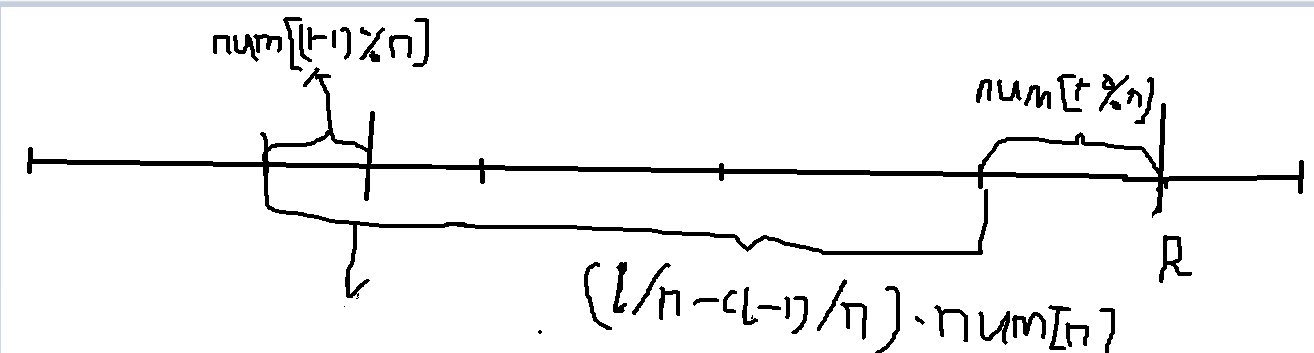
这样应该很明了了，注意处理边界（l-1）;

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const long long Max=1e6+7;
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        ll a,b,q;
        ll num[Max];
        cin>>a>>b>>q;
        ll n=a*b;
        for(int i=1; i<=n; i++)
        {
            num[i]=num[i-1];
            if(i%a%b!=i%b%a)
                num[i]++;
        }
        ll l,r;
        while(q--)
        {
            cin>>l>>r;
            cout<<( r/n - (l-1)/n )*num[n] + num[r%n] - num[(l-1)%n]<<endl;
        }
    }
}