数据结构（七）排序---堆排序

一：定义

作为选择排序的改进版，堆排序可以把每一趟元素的比较结果保存下来，以便我们在选择最小/大元素时对已经比较过的元素做出相应的调整。

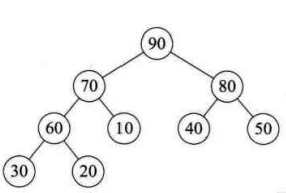
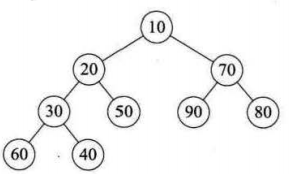
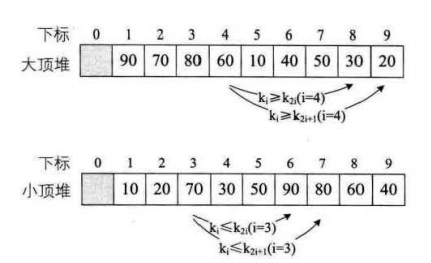
堆排序是一种树形选择排序，在排序过程中可以把元素看成是一颗完全二叉树，每个节点都大（小）于它的两个子节点，当每个节点都大于等于它的两个子节点时，就称为大顶堆，也叫堆有序； 当每个节点都小于等于它的两个子节点时，就称为小顶堆。

下面是我们要保存在数组中的堆的形式

二：堆排序算法

1.将长度为n的待排序的数组进行堆有序化构造成一个大顶堆
 
2.将根节点与尾节点交换并输出此时的尾节点
 
3.将剩余的n -1个节点重新进行堆有序化
 
4.重复步骤2，步骤3直至构造成一个有序序列
 

三：图解演示，构造堆（大顶堆）

{5, 2, 6, 0, 3, 9, 1, 7, 4, 8}

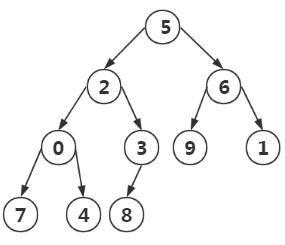
在构造有序堆时，我们开始只需要扫描一半的元素（n/2-1 ~ 0）即可，为什么?

因为(n/2-1)~0的节点才有子节点，如图1，n=8,(n/2-1) = 3  即3 2 1 0这个四个节点才有子节点

第一次找到[n/2]处，进行构造：

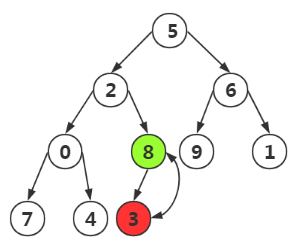
我们比较父节点，左右孩子结点的大小，将最大的作为堆顶

第二次，我们对上次找到位置-1即可，找到结点0，对其左右孩子比较，构造这三个结点的最大堆

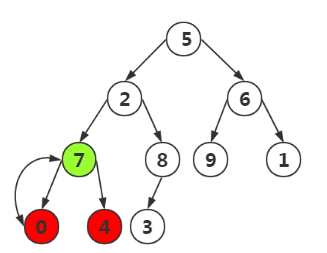
第三次，我们找到结点6，要对其进行构造，结果如下

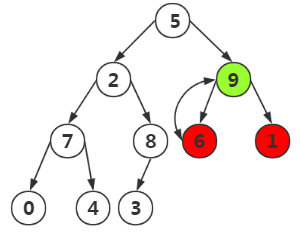
第四次（重点），我们不止要构造双亲和左右孩子，我们还要比较其孩子结点为根的堆是否正确，不然我们需要进行调整

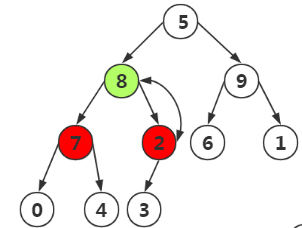
我们发现将8,7,2三个结点变为了最大堆，但是其中2,3子树不再是一个最大堆，我们需要对其修改

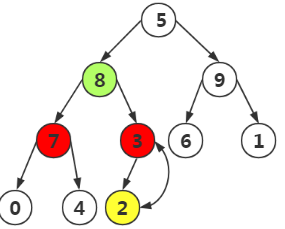
第五次：选取结点9进行构造

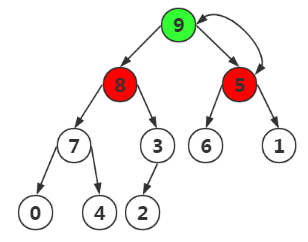
发现以结点5为根的子树不是最大堆，我们需要进行调整

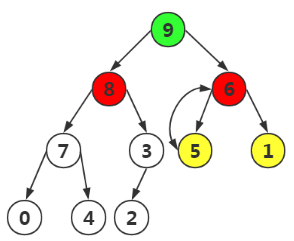
完成最大堆的构建

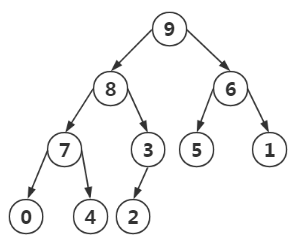
四：图解演示：堆排序（堆存储在数组中）

第一步：将最大值和最后的一个元素交换

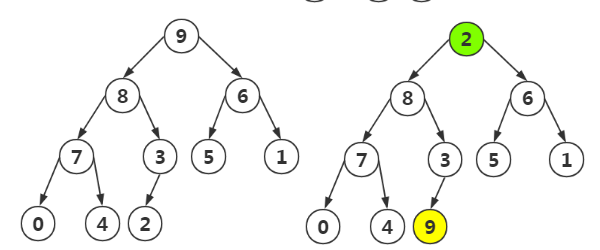
第二步：将剩余的结点再次进行堆构造

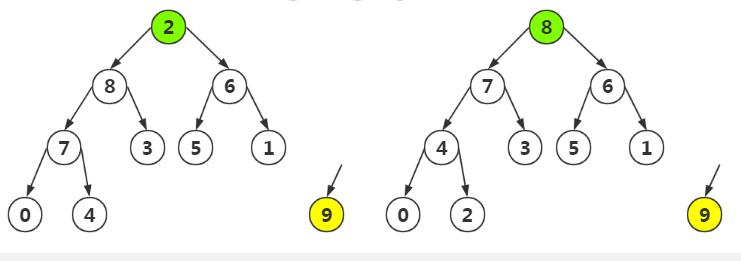
第三步：参照第一步

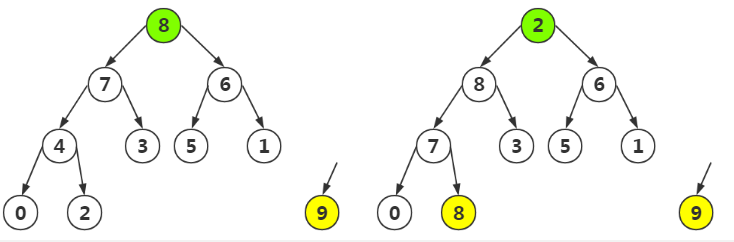
按照上面循环，最终结果为

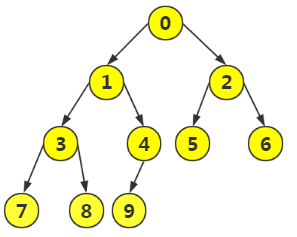
五：代码实现

void swap(int K[], int i, int j)
{
    int temp = K[i];
    K[i] = K[j];
    K[j] = temp;
}

//大顶堆的构造，传入的i是父节点
void HeapAdjust(int k[],int p,int n)
{
    int i,temp;
    temp = k[p];
    for (i = 2 * p; i <= n;i*=2)    //逐渐去找左右孩子结点
    {
        //找到两个孩子结点中最大的
        if (i < n&&k[i] < k[i + 1])
            i++;
        //父节点和孩子最大的进行判断，调整，变为最大堆
        if (temp >= k[i])
            break;
        //将父节点数据变为最大的，将原来的数据还是放在temp中，
        k[p] = k[i];    //若是孩子结点的数据更大，我们会将数据上移，为他插入的点提供位置
        p = i;
    }
    //当我们在for循环中找到了p子树中，满足条件的点，我们就加入数据到该点p,注意：p点原来数据已经被上移动了
    //若没有找到，就是相当于对其值不变
    //插入
    k[p] = temp;
}

//大顶堆排序
void HeapSort(int k[], int n)
{
    int i;
    //首先将无序数列转换为大顶堆
    for (i = n / 2; i > 0;i--)    //注意由于是完全二叉树，所以我们从一半向前构造，传入父节点
        HeapAdjust(k, i, n);

    //上面大顶堆已经构造完成，我们现在需要排序，每次将最大的元素放入最后
    //然后将剩余元素重新构造大顶堆，将最大元素放在剩余最后
    for (i = n; i >1;i--)
    {
        swap(k, 1, i);
        HeapAdjust(k, 1, i - 1);
    }
}


int main()
{
    int i;
    int a[11] = {-1, 5, 2, 6, 0, 3, 9, 1, 7, 4, 8 };
    HeapSort(a, 10);

    for (i = 1; i <= 10; i++)
        printf("%d ", a[i]);

    system("pause");
    return 0;
}

六：性能分析

运行时间主要消耗在构造堆和重建堆时的反复筛选上。
构造堆的时间复杂度为O(n)
重建堆时时间复杂度为O(nlogn)。
所以总体就是O(nlogn)。
不适合排序序列个数较少的情况