------------------------------PCA简单使用------------------------------
一:回顾PCA
(一)主成分分析法是干什么用的?
数据降维,话句话说就是将数据地特征数量变少,但又不是简单地删除特征。
数据降维地目的可以是压缩数据,减少数据的存储空间,让算法提速;
也可以是将数据降到二维或者三维进行可视化
(二)主成分分析法在做什么?
上面说到主成分分析法用于数据降维,大概理解一下它怎么做的。现在我们数据维度为n,我想通过降维让数据变成k维。
那么PCA做的就是对于n维空间的数据,寻找一个K维的“面”,让这些数据到这个“面”的距离最短,这个距离又叫做投影误差。
找到这个“面”后,将n维空间的点投影到这个“面”,因此所有点都投影到了k维空间,因此可以特征数量变为了k。
假设n=2,k=1,那么就是将二维平面上的点投影到一个向量上。假设n=3,k=2,那么就是将三维空间的点投影到一个平面上。
(三)主成分分析法具体怎么做呢?---降维
对于数据要从n维降到k维
首先对数据进行feature scaling/mean normalization,也就是归一化。
其次计算协方差矩阵:(列X行,得矩阵)
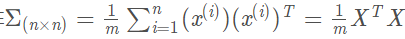
接着计算sigma矩阵的“特征向量”,这里使用奇异值分解(single value decomposition)。SVD奇异值分解得到特征向量和特征值。
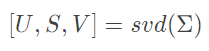
取U矩阵(特征向量矩阵)中前k个向量得到一个n乘k维的矩阵Ureduce,其中训练集x是一个(m,n)矩阵,样本数为m,特征为n维,使用XUreduce就可得到降维后的数据
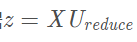
(四)主成分分析法具体怎么做呢?---重建数据
重建数据得到数据的近似值,因为U是特征向量矩阵,它由标准正交基组成,因此U.T@U为单位矩阵,所以这里要重建数据只需
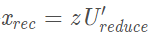
然后再可视化投影,画出标准化的数据以及投影之后又重建的数据,把对应点用虚线连接起来。然后看看降维后的数据保留了原始数据多少的差异性 。
二:数据集导入及可视化
import numpy as np import matplotlib.pyplot as plt import scipy.io as sio data = sio.loadmat("ex7data1.mat") X = data['X'] plt.figure() plt.scatter(X[:,0],X[:,1],marker="X",c="b") plt.show()
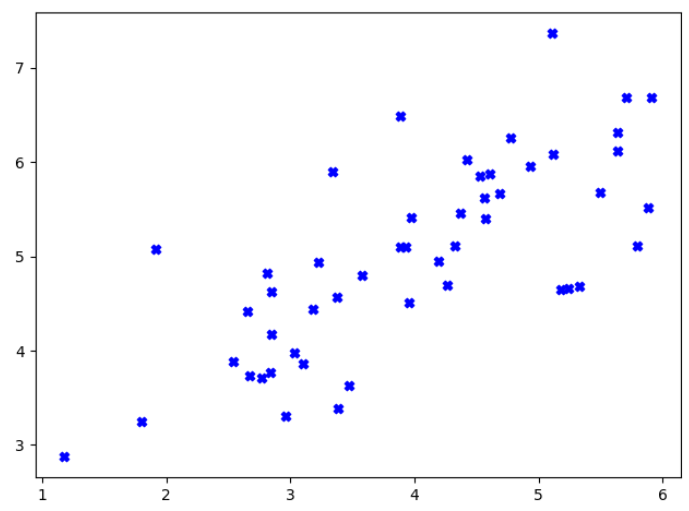
三:数据预处理
实现PCA首先要做的就是对数据的处理进行归一化,注意这里的方差的计算,默认ddof为0,通常情况下是使用ddof=1,就是方差计算中最后除以m还是m-1的不同。ddof=0求解总体标准差,ddof=1求解样本标准差
def data_preprocess(X): #数据预处理 return (X-np.mean(X,axis=0))/np.std(X,axis=0,ddof=1) #对特征进行均值求解(按列)
data = sio.loadmat("ex7data1.mat") X = data['X'] X = data_preprocess(X) print(X)

三:奇异值分解
其次计算协方差矩阵:
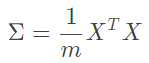
接着计算sigma矩阵的“特征向量”,这里使用奇异值分解(single value decomposition)。SVD奇异值分解得到特征向量和特征值
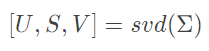
def PCA(X): sigma = X.T.dot(X)/len(X) U,S,V = np.linalg.svd(sigma) return U,S,V
X = data_preprocess(X) U,S,V = PCA(X) print(U) print(S) print(V)

四:使用PCA进行降维
取U矩阵(特征向量矩阵)中前k个向量得到一个n乘k维的矩阵Ureduce,其中训练集x是一个(m,n)矩阵,样本数为m,特征为n维,使用XUreduce就可得到降维后的数据
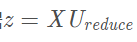
def PCA_process(X,U,K): #进行降维操作 传入的K是我们目标维度 return X.dot(U[:, :K])
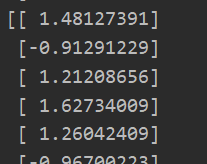
data = sio.loadmat("ex7data1.mat") X = data['X'] X = data_preprocess(X) U,S,V = PCA(X) K = 1 Z = PCA_process(X,U,K) print(Z)
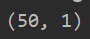
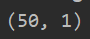
print(Z.shape)
五:数据升维操作
重建数据得到数据的近似值,因为U是特征向量矩阵,它由标准正交基组成,因此U.T@U为单位矩阵,所以这里要重建数据只需
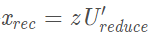
其中z是(m,k)维度,UreduceT是(k,n)矩阵,所以相乘后得到(m,n)维矩阵,达到升维目的。
def reconstruct_data(Z, U, K): #进行升维操作 return Z.dot(U[:,:K].T)
data = sio.loadmat("ex7data1.mat") X = data['X'] X = data_preprocess(X) U,S,V = PCA(X) K = 1 Z = PCA_process(X,U,K) X_approx = reconstruct_data(Z,U,K) print(X_approx)
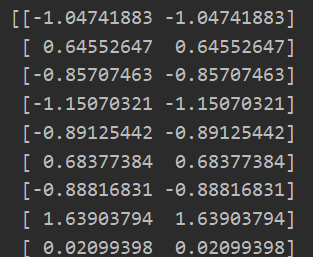
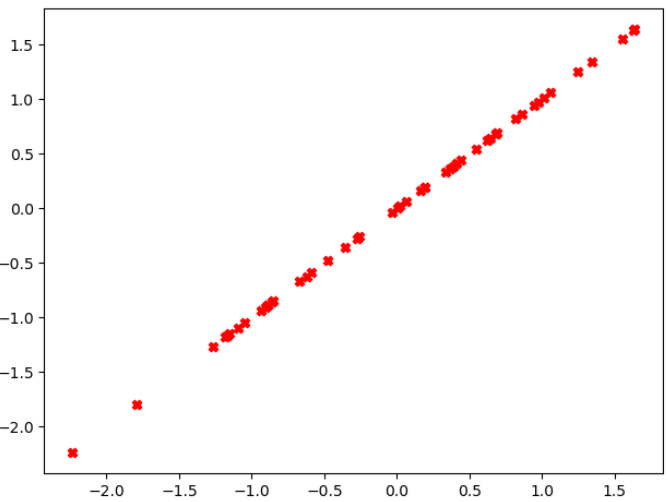
注意:升维后的数据就是在二维空间中的一条直线(降维数据在二维空间的显示)
plt.figure() plt.scatter(X_approx[:,0],X_approx[:,1],marker="X",c="r") #虽然降维到1维,但是我们要画在二维空间中,所以我们需要使用X_approx绘制图像 plt.show()
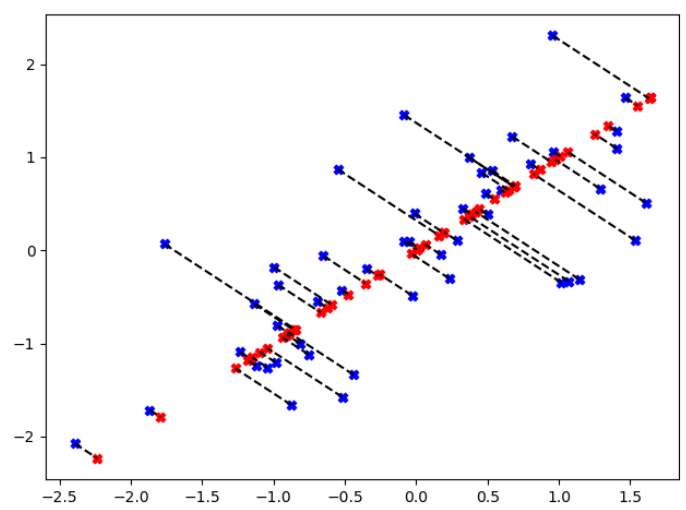
六: 绘制PCA可视化图像
data = sio.loadmat("ex7data1.mat") X = data['X'] X = data_preprocess(X) K = 1 U,S,V = PCA(X) Z = PCA_process(X,U,K) X_approx = reconstruct_data(Z,U,K) plt.figure() plt.scatter(X[:,0],X[:,1],marker="X",c="b") #绘制原图像 plt.scatter(X_approx[:,0],X_approx[:,1],marker="X",c="r") #虽然降维到1维,但是我们要画在二维空间中,所以我们需要使用X_approx绘制图像 #绘制降维路线 for i in range(len(X)): plt.plot([X[i][0],X_approx[i][0]],[X[i][1],X_approx[i][1]],'k--') plt.show()
------------------------------人脸像素降维之PCA使用------------------------------
将PCA应用到人类数据集上,当前的每张人脸图片为1024像素,因此为1024维。我们的目标是将数据降维到36像素,也就是36维。
import numpy as np import matplotlib.pyplot as plt import scipy.io as sio def data_preprocess(X): #数据预处理 return (X-np.mean(X,axis=0))/np.std(X,axis=0,ddof=1) #对特征进行均值求解(按列) def PCA(X): sigma = X.T.dot(X)/len(X) U,S,V = np.linalg.svd(sigma) return U,S,V def PCA_process(X,U,K): #进行降维操作 传入的K是我们目标维度 return X.dot(U[:, :K]) def reconstruct_data(Z, U, K): #进行升维操作 return Z.dot(U[:,:K].T) def visaulizing_images(X,r,d): #r表示显示行数,d表示一行显示图片数 n = X.shape[1] p = int(np.sqrt(n)) for i in range(1,r*d+1): plt.subplot(r,d,i) #m/d行,d列,第i个位置子图 plt.axis("off") #使得每个子图不显示坐标 plt.imshow(X[i-1].reshape(p,p).T,cmap='Greys_r') #人脸数据是倒着的,我们需要转置来摆正 plt.show() data = sio.loadmat("ex7faces.mat") X = data['X'] visaulizing_images(X,2,5) #显示原始图像 X = data_preprocess(X) visaulizing_images(X,2,5) #显示原始图像(归一化后的) K = 36 U,S,V = PCA(X) Z = PCA_process(X,U,K) X_approx = reconstruct_data(Z,U,K) visaulizing_images(X_approx,2,5) #显示原始图像



脸部基本特征还是被保留了。