[学习笔记]线段树优化建边

[算法总结]线段树优化建边

话说ssw02很久以前就用过，当一直没有一个系统的笔记，现在ssw02来补一下

欢迎转载ssw02的博客：https://www.cnblogs.com/ssw02/p/11647181.html

例题引入

POI2015 PUS

题面简化：

给出一个部分未知的数列的长，以及数列已知的部分
再给出一些区间。对于每一个区间，在它的内部钦定一些位置，并要求这些位置上的数最后的值，都严格大于区间内其他未钦定的位置上的数。
要求给出任意一种可行的满足条件的数列。

我们发现，选择的点和不选择的点之间有一定的等级关系，而且题目开启了 spj ，所以我们只要把等级关系放在图上然后跑拓扑即可。

然后我们考虑到暴力建边：但这样的负载显然承受不住，N^2的边数没有任意一种算法可以计算。

但是这道题有一个性质，我们的点都是向一个区间连接边权都为1的边。正是因为这些区间有大多数相交，才导致我们的时空复杂度都超出限制。那么我们不妨想想，有什么可以大幅提高区间操作的效率---线段树。

然后我们考虑到线段树优化建边。建边的方式是通过一个点向一个区间连边时，将区间放在线段树中，分割为最多log区间。同时线段树的区间还要向其子区间连边。

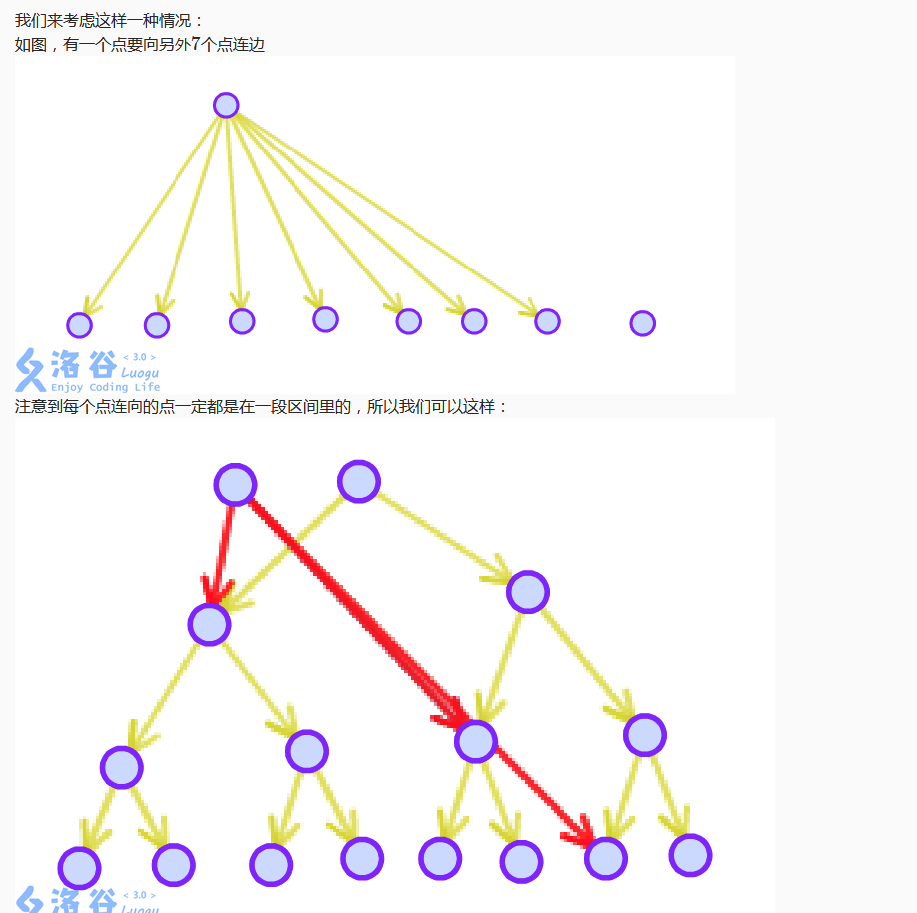
这幅来自洛谷的图很好的诠释了线段树优化建边的性质，只是边少，效果不明显。

由于一个区间被分给为最多log条区间，加上我们之前线段树建图的 4N（开两倍）边，总变数不超过 NlogN 级别。

然后跑一个拓扑排序，游戏结束

代码 PUS

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN = 100005;
const int MAXM = 200000+300005 ;
int N , M , S ;
inline int read(){
	int s=0 ; char g=getchar() ; while(g>'9'||g<'0')g=getchar() ; 
	while(g>='0'&&g<='9')s=s*10+g-'0',g=getchar() ; return s ;
}
int head[ MAXM ] , to[ MAXM ] , nex[ MAXM ] , w[ MAXM ] , tot =1 , cnt;
int id[ MAXN ] ;
bool vis[MAXM];
int du[ MAXM ] , dis[ MAXM ] , val[ MAXM ] ;
struct Seg{
	int ls , rs ;
}t[ MAXN<<2 ] ;
queue<int>q ;
void  add( int x , int y , int z ){
	to[ ++tot ] = y , nex[ tot ] = head[ x ] , w[ tot ] = z , head[ x ] = tot ;
}
void build( int p , int l , int r ){
    if( l == r ) {
        id[ l ] = p ;return; //反向记录 l 点在线段树中对应的节点 
    }
    int mid = (l+r)>>1 ;
    t[ p ].ls = ++cnt , du[ p ]++ ; add( cnt , p , 0 ) ; 
    t[ p ].rs = ++cnt , du[ p ]++ ; add( cnt , p , 0 ) ; 
    build( t[ p ].ls , l , mid ) ;
    build( t[ p ].rs , mid+1 , r ) ;
}
void updata( int p , int l , int r , int x , int y , int to ){
    if( x > y )return ;
    if( x <= l && r <= y ){
        add( p , to , 1 ) ; du[ to ]++ ;
        return;
    }
    int mid = ( l+r )>>1 ; 
    if( x <= mid )updata( t[p].ls , l , mid , x , y , to ) ;
    if( mid < y )updata( t[p].rs , mid+1 , r , x , y , to ) ;
}
bool toposort(){
    memset( dis , 0xcf , sizeof(dis) ) ;
    for( int i = 1 ; i <= cnt ; ++i ){
        if( du[ i ] == 0 ){
            if( val[i] )dis[ i ] = val[ i ] ;
            else dis[ i ] = 1 ;
            vis[ i ] = true ; q.push( i ) ; 
        }
    }
    while( !q.empty() ){
        int u = q.front() ; vis[ u ] = true ; q.pop() ;
        for( int i = head[ u ] ; i ; i = nex[ i ] ){
            du[ to[i] ]-- ;
            if( dis[ to[i] ] < dis[ u ] + w[ i ] )dis[ to[i] ] = dis[ u ] + w[ i ] ;
            if( du[ to[i] ] == 0 ){
                if( val[ to[i] ] ){//我们给定的限制 
                    if( val[ to[i] ] < dis[ to[i] ]) return false;
                    else dis[ to[i] ] = val[ to[i] ] ;
                }
                q.push( to[i] ) ;
            }
        }
    }
    for( int i=1;i<=cnt;++i){
        if( !vis[ i ] ) return false;
        if( dis[ i ] > 1e9 ) return false;
    }
    return true;
}
int main(){
    N = read() , S = read() , M = read() ;int m1 , m2 , m3 ;
    ++cnt ;
    build( 1 , 1 , N ) ;
    for( int i =  1 ; i <= S ; ++i ){
        m1 = read() , m2 = read() ;
        val[ id[m1] ] = m2 ;
    }
    int las = 0 , l , r , k ;
    for( int i = 1 ; i <= M ; ++i ){
        l = read() , r = read() , k = read() , cnt++ ;
        las = l - 1 ;
        while( k-- ){
            m1 = read() ;
            updata( 1 , 1 , N , las+1 , m1-1 , cnt ) ;// p , l , r , x , y , target 
            add( cnt , id[ m1 ] , 0 ) ; 
			du[ id[m1] ]++ , las = m1 ;
        }
        updata( 1 , 1 , N , las+1 , r , cnt ) ;
    }
    bool flag = toposort() ;//是否无解 
    if( !flag )printf("NIE") ;
    else {
        printf("TAK
");
        for( int i = 1 ; i <= N ; ++i )printf("%d ",dis[ id[i] ] ) ;
    }
    return 0;
}

然后再放一个maho烧酒馒头卡的代码，由于体面私有问题(SXK：我打死你)，将这道模板放在这里。

#include<bits/stdc++.h>
using namespace std ;
#define ll long long
const int MAXN = 100005 , MAXM = 100005*18 ;
inline int read(){
	int s=0 ; char g=getchar() ; while( g>'9'||g<'0' )g=getchar() ; 
	while(g>='0'&&g<='9')s=s*10+g-'0',g=getchar() ; return s ;
}
int  head[ MAXN<<2 ] , to[ MAXM ] , nex[ MAXM ] , w[ MAXM ] , tot = 1 ;
int  N , a[ MAXN ], id[ MAXN ] , cnt = 0 , rt ;
ll f[ MAXM ] ;
bool vis[ MAXM ] ;
struct Seg{
	int ls , rs ;
}t[ MAXN<<2 ] ;
priority_queue< pair<ll,int> >q ; 
void  add( int x , int y , int z ){
	to[ ++tot ] = y , nex[ tot ] = head[ x ] , w[ tot ] = z , head[ x ] = tot ;
}
int  build( int &p , int l , int r ){
	if( !p )p = ++cnt ;
	if( l == r ){
		id[ l ] = p ; return  true ;
	}
	int mid = ( l+r )>>1 ;
	if( build( t[ p ].ls , l , mid ) )add( p , t[ p ].ls , a[l] ) ;
	else add( p , t[ p ].ls , 0 ) ;
	if( build( t[ p ].rs , mid+1 , r ) )add( p , t[ p ].rs , a[r] ) ;
	else add(  p , t[ p ].rs  , 0 ) ;
	return false ;
}
void  updata( int p , int l , int r , int x , int y , int pre ){
	if( x <= l && r <= y ){
		if( l == r )add( id[pre] , p , a[l]+a[pre] ) ;
		else add( id[pre] , p , a[pre] ) ; return ;
	}
	int mid = ( l+r )>>1;
	if( x <= mid )updata( t[ p ].ls , l , mid , x , y , pre ) ;
	if( y > mid )updata( t[ p ].rs , mid+1 , r , x , y , pre ) ;
}
void  dijkstra(){
	for( int i = 1 ; i <= N*18 ; ++i )f[ i ] = (1LL<<40) ; f[ id[1] ] = 0 ;
	q.push( make_pair( 0 , id[1] ) ) ; vis[ id[1] ] = true ;
	while( !q.empty() ){
		int u = q.top().second ; q.pop() ; vis[ u ] = false ;
		for( int i = head[ u ] ; i ; i = nex[ i ] )
			if( f[ to[i] ] > f[ u ] + w[ i ] ){
			    f[ to[i] ] = f[ u ] + w[ i ] ;
			    if( !vis[ to[i] ] ){
			   	    q.push( make_pair( -f[ to[i] ] , to[i] ) ) ; vis[ to[i] ] = true ;
			    }
			}
	}
}
int main(){
	N = read() ; int m1 , m2 ;
	for( int i = 1 ; i <= N ; ++i )a[ i ] = read() ;
	m1 = build( rt , 1 , N ) ; 
	for( int i = 1 ; i <= N ; ++i ){
		m1 = read() , m2 = read() ;
		updata( rt , 1 , N , m1 , m2 , i ) ;
	}
	dijkstra() ;
	for( int i = 1 ; i <= N ; ++i )printf("%lld
",(f[id[i]]==(1LL<<40))?-1:f[ id[i] ] ) ;
	return 0 ;
}

欢迎转载ssw02的博客：https://www.cnblogs.com/ssw02/p/11647181.html