题目描述
对于1 位二进制变量定义两种运算:
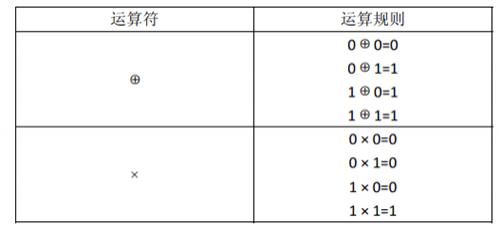
运算的优先级是:
-
先计算括号内的,再计算括号外的。
- “× ”运算优先于“⊕”运算,即计算表达式时,先计算× 运算,再计算⊕运算。例如:计算表达式A⊕B × C时,先计算 B × C,其结果再与 A 做⊕运算。
现给定一个未完成的表达式,例如_+(_*_),请你在横线处填入数字0 或者1 ,请问有多少种填法可以使得表达式的值为0 。
输入输出格式
输入格式:
输入文件名为exp.in ,共 2 行。
第1 行为一个整数 L,表示给定的表达式中除去横线外的运算符和括号的个数。
第2 行为一个字符串包含 L 个字符,其中只包含’(’、’)’、’+’、’*’这4 种字符,其中’(’、’)’是左右括号,’+’、’*’分别表示前面定义的运算符“⊕”和“×”。这行字符按顺序给出了给定表达式中除去变量外的运算符和括号。
输出格式:
输出文件exp.out 共1 行。包含一个整数,即所有的方案数。注意:这个数可能会很大,请输出方案数对10007 取模后的结果。
输入输出样例
说明
【输入输出样例说明】
给定的表达式包括横线字符之后为:_+(_*_)
在横线位置填入(0 、0 、0) 、(0 、1 、0) 、(0 、0 、1) 时,表达式的值均为0 ,所以共有3种填法。
【数据范围】
对于20% 的数据有 0 ≤ L ≤ 10。
对于50% 的数据有 0 ≤ L ≤ 1,000。
对于70% 的数据有 0 ≤ L ≤ 10,000 。
对于100%的数据有 0 ≤ L ≤ 100,000。
对于50% 的数据输入表达式中不含括号。
开始写的区间dp....我真是菜
然后借鉴candy大神的blog
笛卡尔树建表达式树,然后树形dp
dp[i][1/0]表示根节点为i的区间值为1/0的方案数
#include<algorithm> #include<iostream> #include<cstring> #include<cstdio> #include<cmath> using namespace std; const int N=100007,MOD=10007; int n; char s[N]; struct node{ int l,r; char op; }tree[N]; int cnt=0,w[N],root=0; void build(){ int p=0,cnt=0; for(int i=1;i<=n;i++){ if(s[i]=='(') p++;if(s[i]==')') p--; if(s[i]=='+') {w[++cnt]=p*2+1; tree[cnt].op=s[i]; } if(s[i]=='*') w[++cnt]=p*2+2,tree[cnt].op=s[i];; } int st[N],k,top=-1; for(int i=1;i<=cnt;i++) { k=top; while(k>=0&&w[st[k]]>w[i]) k--; if(k!=-1)tree[st[k]].r=i; if(k<top) tree[i].l=st[k+1]; st[++k]=i; top=k; } root=st[0]; } int f[N][2]; void dp(int i) { if(i==0) return; if(f[i][0]!=0) return; int l=tree[i].l,r=tree[i].r;char op=tree[i].op; dp(l);dp(r); if(op=='+'){ f[i][0]=f[l][0]*f[r][0]; f[i][1]=f[l][0]*f[r][1]+f[l][1]*f[r][0]+f[l][1]*f[r][1]; } if(op=='*'){ f[i][1]=f[l][1]*f[r][1]; f[i][0]=f[l][0]*f[r][1]+f[l][1]*f[r][0]+f[l][0]*f[r][0]; } f[i][1]%=MOD;f[i][0]%=MOD; } int main() { scanf("%d",&n); scanf("%s",s+1); build(); f[0][0]=f[0][1]=1; dp(root); printf("%d",f[root][0]%MOD); return 0; }