忍者钩爪
题目描述
小 Q 是一名酷爱钩爪的忍者, 最喜欢飞檐走壁的感觉, 有一天小 Q 发现一个练习使用钩
爪的好地方,决定在这里大显身手。
场景的天花板可以被描述为一个无穷长的数轴, 初始小 Q 挂在 原点上。 数轴上有 N 个坐
标为整数的圆环供小 Q 实现钩爪移动。具体操作为:小 Q 可以将钩爪挂到圆环上,进而荡到
关于圆环坐标 轴对称的位置。例如小 Q 在 3,圆环在 7,则小 Q 可以通过该圆环移动到 11。
现在一个问题难倒了小 Q,如何判断自己能否到达某个整点呢?
输入格式
第一行两个整数 N,M,表示圆环的数量和询问组数
接下来一行共 N 个整数描述每个圆环的坐标(可重复)
接下来 M 行每行包含一个整数描述询问
输出格式
共 M 行对应 M 个询问,若小 Q 能移动到目标点,输出 Yes,否则输出 No
样例
2 2
1 3
3
4
No
Yes
数据范围
对于 30%的数据,M≤N≤10,输入坐标绝对值均小于 1000。
对于 60%的数据,M≤N≤5000。
对于 100%的数据,M≤N≤100000,输入坐标绝对值均小于 (10^{18})。
随手写了个60的做法,然后跑去写T2,然后脑残的YES,NO输成全大写了
画图选点推式子可得它可到达的坐标距离为(x+2*(a[i]-a[j])), x为当前坐标那么
初始坐标为原点,那么奇数坐标是肯定不能到达的QAQ
根据广义裴蜀定理以及扩展欧几里得相关原理可知,当且仅当目标为gcd的倍数时有解。
故预处理出全部可能的2(a[j]-a[i]),求出其最大公约数,在判断目标是否为gcd的倍数即可复杂度N^2可拿60分
通过欧几里得算法的性质与更相减损术可知gcd(a,b)=gcd(a-b,b)。
设p1={2(a[i]-a[1])|i>1}的最大公约数,设p2={2(a[i]-a[j])}的最大公约数,易知p1>=p2(因为p1比p2约束宽松)
而对于任意i,j由于p1同时是2(a[i]-a[1])、2(a[j]-a[1])的约束,那么p1也一定是任意2(a[i]-a[1])-2(a[j]-a[1])=2*(a[i]-a[j])的约数,故p1<=p2。综上所述p1=p2,
这样就不需要N^2个数同时求gcd了,只求p1即可,可获得满分。
code:
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 2000007;
#define LL long long
int n,m,cnt=0;
LL a[maxn];
LL g;
LL gcd(LL x,LL y) {
if(y==0)return x;
else return gcd(y,x%y);
}
int main () {
int c1=0,c2=0;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) {
LL aa;
scanf("%lld",a+i);
}
g=2*(a[1]-a[2]);
for(int i=1;i<=n;i++) g=gcd(g,2*(a[i]-a[1]));
for(int i=1;i<=m;i++) {
LL q;
scanf("%lld",&q);
if((q%g+g)%g==0&&q%2==0)puts("Yes");
else puts("No");
}
return 0;
}
选球游戏
题目描述
华华和秀秀在玩游戏。在他们面前有!个球排成一排,从左到右按 1 到!编号。每个球有一
个可正可负的权值。 每一轮, 秀秀会选定一个区间([l,r]),将编号在这个区间内的所有球的权值
加上一个值(c), 或者将编号在这个区间内的所有球的权值都设为其相反数。 华华则需从这!个球
中选出k个球来,他的得分为这k个球的权值的乘积。
华华每次都能快快地找出得分最优的选球方案来。秀秀想了想,决定提升游戏难度。她每
次会选定一个区间([l,r]),然后询问华华在这个区间内选出(k(1 ≤ k ≤ 10))个球的所有方案的得
分之和。
这下可把华华难倒了,于是华华找到了聪明的你。你能帮帮他嘛?
由于所有方案的得分之和可能很大,你只需要输出得分之和对(1000000007(10 / + 7))取模
的结果(负数请加上(10 / + 7)变成非负数)即可。
输入格式
从文件game.in 中读入数据。
输入第一行包含两个正整数!,1,分别表示球的个数和秀秀的操作条数。
接下来一行包含!个空格隔开的整数,表示每个球初始的权值。
接下来1行,每行表示秀秀的一个操作。
若该行形如“(1 l r c)”,则表示秀秀将编号属于([l,r])的所有球的权值都加上了c;
若该行形如“(2 l r)”,则表示秀秀将编号属于([l,r])的所有球的权值都置为了其相反数;
若该行形如“(3 l r k)”,则表示华华需要回答从([l,r])中选出k个球的所有取球方案的得分之和。
输出格式
输出文件到(game.out)中。
对于秀秀宝宝的每一个询问操作,输出一行,表示该询问的答案。
样例
10 9
3 6 7 4 6 1 6 7 2 6
3 5 7 3
1 1 7 -9
1 2 3 5
3 2 6 1
2 5 8
3 5 7 3
2 2 3
3 1 10 2
3 1 2 2
36
999999996
72
999999885
12
【样例说明】
第一个询问:(6×1×6 = 36)
第二个询问:
询问前各个球的权值为:(-6 2 3 -5 -3 -8 -3 7 2 6)
(2 + 3 + ?5 + ?3 + ?8 = ?11)
(?11 + (10 / + 7) = 999999996)
第三个询问:
询问前各个球的权值为:(-6 2 3 -5 3 8 3 7 2 6)
(3×8×3 = 72)
【子任务】
子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难,可以尝试只解决一
部分测试数据。每个测试点的规模及特点如下表:
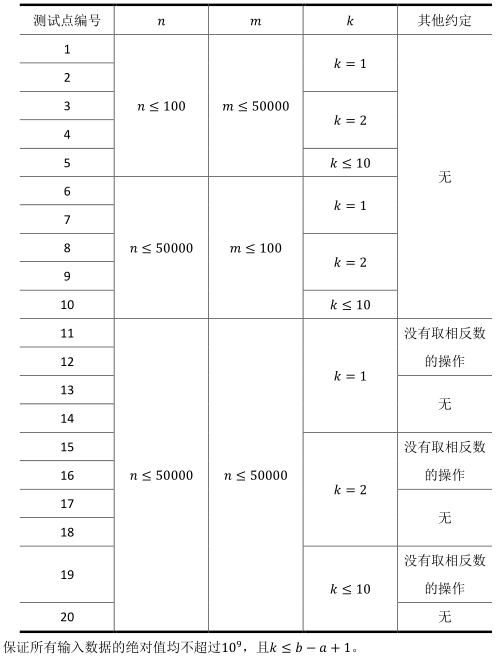
用线段树。对于每个节点我们维护一个f[i][j],表示这个节点i所对应区间选j个球的答案。
考虑如何合并两个节点f[i][j] = sum(f[leftson] [i]* f[rightson][i-j]) 即sum(区间f[0,i]*f[0,i]/f[1,j])
对于取相反数操作,只有当i是奇数时,才会改变f[i]的符号。 对于一段区间+c的操作,设这段区间的长度为len,
则新的f[RT][i]为sum (fRT * c^{i,j} * C(len - j, i - j)) jin [0,i] 其中C(n,m)当然是组合数啦
这样我们就可以套用区间修改区间询问的线段树来解决这道题了,时间复杂度为O(c^2nlogn),然而我写的sds被卡常了,orz
卡常code
#include<cstdio>
#include<algorithm>
using namespace std;
#define LL long long
inline int read() {
int x=0,f=1;
char cc=getchar() ;
while(cc<'0'||cc>'9'){if(cc=='-')f=-1;cc=getchar();};
while(cc<='9'&&cc>='0')x=x*10+cc-'0',cc=getchar();return x*f;
}
const int maxn = 0007;
const int mod = 1000000007;
int n,m;
LL tree[maxn<<2][15],a[maxn],lazy1[maxn<<2],lazy2[maxn<<2];
LL C[maxn][25];
inline void merge(int rt)
{
for(int i=0;i<=10;++i)
{
tree[rt][i]=0;
for(int j=0;j<=i;j++)
tree[rt][i]=(tree[rt][i]+tree[rt<<1][j]*tree[rt<<1|1][i-j]%mod)%mod;
}
}
void update(int l,int r,int rt,int w)
{
int len=(r-l)+1;
LL tmp[11];
for(int i=0;i<=10;i++)tmp[i]=tree[rt][i]%mod;
for(int i=1;i<=10;i++)
{
tree[rt][i]=0;
LL t=1;
for(int j=0;j<=i;++j)
{
LL tt=tmp[i-j]%mod*C[len-(i-j)][j]%mod*t%mod;
tree[rt][i]=(tree[rt][i]+tt)%mod;
t=(t%mod)*(w%mod)%mod;
}
}
return ;
}
void pushdown(int l,int r,int rt)
{
int mid=(l+r)>>1;
if(lazy1[rt])
{
if(lazy2[rt<<1])lazy1[rt<<1]=(lazy1[rt<<1]+mod-lazy1[rt])%mod;
else lazy1[rt<<1]=(lazy1[rt<<1]+lazy1[rt])%mod;
if(lazy2[rt<<1|1])lazy1[rt<<1|1]=(lazy1[rt<<1|1]+mod-lazy1[rt])%mod;
else lazy1[rt<<1|1]=(lazy1[rt<<1|1]+lazy1[rt])%mod;
update(l,mid,rt<<1,lazy1[rt]);
update(mid+1,r,rt<<1|1,lazy1[rt]);
lazy1[rt]=0;
}
if(lazy2[rt])
{
for(int i=1;i<=10;i+=2)
{
tree[rt<<1][i]=mod-tree[rt<<1][i];
tree[rt<<1|1][i]=mod-tree[rt<<1|1][i];//翻转
}
lazy2[rt]=0;
lazy2[rt<<1]^=1;
lazy2[rt<<1|1]^=1;
}
}
void build(int l,int r,int rt)
{
if(l==r)
{
for(int i=0;i<=10;i++)tree[rt][i]=0;
tree[rt][0]=1;
tree[rt][1]=(a[l]%mod+mod)%mod;
return ;
}
int mid=(l+r)>>1;
build(l,mid,rt<<1);
build(mid+1,r,rt<<1|1);
merge(rt);
}
void modify1(int l,int r,int rt,int tl,int tr,int tw)
{
if(tl<=l&&tr>=r)
{
if(lazy2[rt])lazy1[rt]=(lazy1[rt]+mod-tw)%mod;//有反转标记时减去
else lazy1[rt]=(lazy1[rt]+tw)%mod;
update(l,r,rt,tw);return ;
}
pushdown(l,r,rt);
int mid=(l+r)>>1;
if(tl<=mid)modify1(l,mid,rt<<1,tl,tr,tw);
if(tr>mid)modify1(mid+1,r,rt<<1|1,tl,tr,tw);
merge(rt);
return ;
}
void modify2(int l,int r,int rt,int tl,int tr)
{
if(tl<=l&&tr>=r)
{
for(int i=1;i<=10;i+=2)tree[rt][i]=mod-tree[rt][i];//反转操作
lazy2[rt]^=1;
return ;
}
pushdown(l,r,rt);
int mid=(l+r)>>1;
if(tl<=mid)modify2(l,mid,rt<<1,tl,tr);
if(tr>mid)modify2(mid+1,r,rt<<1|1,tl,tr);
merge(rt);
}
struct Node{
LL f[14];
};
Node calc(Node lc,Node rc)
{
Node o;
o.f[0]=1;
for(int i=1;i<=10;i++)
{
o.f[i]=0;
for (int j=0;j<=i;j++)
o.f[i]=(o.f[i]+lc.f[j]*rc.f[i-j]%mod)%mod;
}
return o;
}
Node query(int l,int r,int rt,int tl,int tr)
{
if(tl<=l&&tr>=r)
{
Node a;
for(int i=0;i<=10;++i)a.f[i]=tree[rt][i];
return a;
}
int mid=(l+r)>>1;
pushdown(l,r,rt);
if(tr<=mid)return query(l,mid,rt<<1,tl,tr);
if(tl>mid)return query(mid+1,r,rt<<1|1,tl,tr);
Node lc=query(l,mid,rt<<1,tl,tr);
Node rc=query(mid+1,r,rt<<1|1,tl,tr);
return calc(lc,rc);
}
int main ()
{
n=read(),m=read();
C[0][0]=1;
for (int i=1;i<=n;i++)
{
C[i][0]=1;
for (int j=1;j<=10;j++)
C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
}
for(int i=1;i<=n;i++)a[i]=read();
build(1,n,1);
for(int id,a,b,c;m--;)
{
id=read(),a=read(),b=read();
if(id==1)
{
c=read();modify1(1,n,1,a,b,c);
}
else if(id==2)
{
modify2(1,n,1,a,b);
}
else if(id==3)
{
c=read();
Node tmp=query(1,n,1,a,b);
printf("%d
",(tmp.f[c]+mod)%mod);
}
}
}
/*
10 9
3 6 7 4 6 1 6 7 2 6
3 5 7 3
1 1 7 -9
1 2 3 5
3 2 6 1
2 5 8
3 5 7 3
2 2 3
3 1 10 2
3 1 2 2
36
999999996
72
999999885
12
*/
std:当然不是我写的QAQ
#include <cstdio>
#include <cstdlib>
#define MOD 1000000007
#define N 100005
typedef long long LL;
using namespace std;
struct Node {
LL f[11];
}node[N * 4];
LL a[N], lazy1[N * 4];
bool lazy2[N * 4];
LL C[N][11];
Node merge(Node lc, Node rc) {
Node o;
o.f[0] = 1;
for (int i = 1; i <= 10; i++) {
o.f[i] = 0;
for (int j = 0; j <= i; j++)
o.f[i] = (o.f[i] + lc.f[j] * rc.f[i - j] % MOD) % MOD;
}
return o;
}
void build(int o, int l, int r) {
if (l == r) {
for (int i = 0; i <= 10; i++) node[o].f[i] = 0;
node[o].f[0] = 1;
node[o].f[1] = (a[l] % MOD + MOD) % MOD;
return ;
}
int mid = (l + r) >> 1;
build(o * 2, l, mid);
build(o * 2 + 1, mid + 1, r);
node[o] = merge(node[o * 2], node[o * 2 + 1]);
return ;
}
void update1(int o, int l, int r, int c) {
int len = r - l + 1;
LL ff[11];
for (int i = 0; i <= 10; i++) ff[i] = node[o].f[i];
for (int i = 1; i <= 10; i++) {
node[o].f[i] = 0;
LL t = 1;
for (int j = 0; j <= i; j++) {
LL tmp = ff[i - j] * C[len - (i - j)][j] % MOD * t % MOD;
node[o].f[i] = (node[o].f[i] + tmp) % MOD;
t = t * c % MOD;
}
}
return ;
}
void push_down(int o, int l, int r) {
int mid = (l + r) >> 1;
if (lazy1[o]) {
if (lazy2[o * 2])
lazy1[o * 2] = (lazy1[o * 2] + MOD - lazy1[o]) % MOD;
else
lazy1[o * 2] = (lazy1[o * 2] + lazy1[o]) % MOD;
if (lazy2[o * 2 + 1])
lazy1[o * 2 + 1] = (lazy1[o * 2 + 1] + MOD - lazy1[o]) % MOD;
else
lazy1[o * 2 + 1] = (lazy1[o * 2 + 1] + lazy1[o]) % MOD;
update1(o * 2, l, mid, lazy1[o]);
update1(o * 2 + 1, mid + 1, r, lazy1[o]);
lazy1[o] = 0;
}
if (lazy2[o]) {
lazy2[o * 2] ^= 1;
lazy2[o * 2 + 1] ^= 1;
for (int j = 1; j <= 10; j += 2) {
node[o * 2].f[j] = MOD - node[o * 2].f[j];
node[o * 2 + 1].f[j] = MOD - node[o * 2 + 1].f[j];
}
lazy2[o] = 0;
}
}
void modify1(int o, int l, int r, int ll, int rr, int c) {
if (ll <= l && rr >= r) {
if (lazy2[o]) lazy1[o] = (lazy1[o] + MOD - c) % MOD;
else lazy1[o] = (lazy1[o] + c) % MOD;
update1(o, l, r, c);
return ;
}
int mid = (l + r) >> 1;
push_down(o, l, r);
if (ll <= mid) modify1(o * 2, l, mid, ll, rr, c);
if (rr > mid) modify1(o * 2 + 1, mid + 1, r, ll, rr, c);
node[o] = merge(node[o * 2], node[o * 2 + 1]);
return ;
}
void modify2(int o, int l, int r, int ll, int rr) {
if (ll <= l && rr >= r) {
for (int i = 1; i <= 10; i += 2) node[o].f[i] = MOD - node[o].f[i];
lazy2[o] ^= 1;
return ;
}
int mid = (l + r) >> 1;
push_down(o, l, r);
if (ll <= mid) modify2(o * 2, l, mid, ll, rr);
if (rr > mid) modify2(o * 2 + 1, mid + 1, r, ll, rr);
node[o] = merge(node[o * 2], node[o * 2 + 1]);
return ;
}
Node query(int o, int l, int r, int ll, int rr) {
if (ll <= l && rr >= r)
return node[o];
int mid = (l + r) >> 1;
push_down(o, l, r);
if (rr <= mid) return query(o * 2, l, mid, ll, rr);
if (ll > mid) return query(o * 2 + 1, mid + 1, r, ll, rr);
Node lc = query(o * 2, l, mid, ll, rr);
Node rc = query(o * 2 + 1, mid + 1, r, ll, rr);
return merge(lc, rc);
}
int main(int argc, char ** argv) {
//freopen("game.in", "r", stdin);
//freopen("game.out", "w", stdout);
int n, m;
scanf("%d %d", &n, &m);
C[0][0] = 1;
for (int i = 1; i <= n; i++) {
C[i][0] = 1;
for (int j = 1; j <= 10; j++)
C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % MOD;
}
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]);
build(1, 1, n);
for (int i = 1; i <= m; i++) {
int l, r, opt;
scanf("%d%d%d",&opt, &l, &r);
if (opt == 1) {
int c;
scanf("%d", &c);
c = (c % MOD + MOD) % MOD;
modify1(1, 1, n, l, r, c);
}
else if (opt == 2) {
modify2(1, 1, n, l, r);
}
else {
int k;
scanf("%d", &k);
Node o = query(1, 1, n, l, r);
printf("%d
", o.f[k] % MOD);
}
}
return 0;
}
川川的漫步
题目描述
金秋时分,T大的校园里色彩斑斓。校园的景色可以被看成(n)个点,每个点会被赋予一个(0)到(d-1)之间的整数,
表示这个景点的类型。校园里阡陌交通,大一新生川川第一时刻在景点1.然后他开始随意的漫步,假设某时刻他在第i个景点
,则下一时刻,川川会以概率(p_{ij})移动到景点(j)(保证(sum_{j=1}^n p_{ij}=1))。在漫步N个时刻之后,川川会
把他所经过的景点类型全部记下来,这样他会得到一个长度为N的数列(S),(S)中每个数都在(0)到(d-1)之间。
川川很想研究,他最后得到的数列的概率分布,。假设他所有可能得到的数列为(S_1,S_2,cdots ,S_m)。令
(q_i=P_r[S=S_i],i=1,2,cdots,m)
表示他得到的数列是(S_i)的概率。
作为能考上(T)大的学生,川川当然知道,(sum_{i=1}^m q_i=1),但这对他探究S的概率分布毫无帮助。
现在,请你帮他计算出
输入格式
第一行两个数(n)和(N),表示景点个数和川川总共要走的时刻数。接下来(n)行,每行(n)个数,第(i)行第(j)个数字
表示(p_{ij})。输入数据保证对任意的(i),(sum_{j=1}^n p_{ij}=1)。接下来一行一个数,(d),表示井底那的类型书。
再接下来一行(n)个(0)到(d-1)之间的数,一次表示每个景点的类型。
输出格式
一行,表示(sum_{i=1}^m q_i^2)的值,保留九位小数。
样例
2 2
0.5 0.5
0.5 0.5
2
0 1
0.500000000
3 3
0.2 0.4 0.4
1 0 0
1 0 0
2
0 1 1
0.667200000
数据范围
对于(30\%)的数据,$ Nleq 10,dleq 3 $。
对于(50\%)的数据,$ Nleq 50 $。
对于(100\%)的数据,$ n,mleq 16,Nleq 10^{18},dleq 100 $。