ST (Sparse Table：稀疏表)算法

1541：【例 1】数列区间最大值

时间限制: 1000 ms         内存限制: 524288 KB
提交数: 600     通过数: 207 

【题目描述】

输入一串数字，给你 MM 个询问，每次询问就给你两个数字 X,YX,Y，要求你说出 XX 到 YY 这段区间内的最大数。

【输入】

第一行两个整数 N,MN,M 表示数字的个数和要询问的次数；

接下来一行为 NN 个数；

接下来 MM 行，每行都有两个整数 X,YX,Y。

【输出】

输出共 MM 行，每行输出一个数。

 

【输入样例】

10 2
3 2 4 5 6 8 1 2 9 7
1 4
3 8

【输出样例】

5
8

【提示】

数据范围与提示：

对于全部数据，1≤N≤105,1≤M≤106,1≤X≤Y≤N1≤N≤105,1≤M≤106,1≤X≤Y≤N。数字不超过 C/C++C/C++ 的 intint 范围。

【来源】http://ybt.ssoier.cn:8088/problem_show.php?pid=1541

解析：  这是指求区间最值的模板问题，这里采用 ST算法来实现,总的时间复杂度O(nlogn+Q)
。

倍增思想：

f[i][j]表示i开始的连续2^j 个点的最大值。

则f[i][0]表示i开始连续1个点的最大值即a[i];

f[i][1]表示i开始连续2个点的最大值即a[i]和a[i+1]的最大值;

f[i][2]表示i开始连续4个点的最大值即a[i]~a[i+3]中的最大值；

f[i][3]表示i开始连续8个点的最大值即a[i]~a[i+7]中的最大值;

 ......

f[i][log(n)/log(2)开始连续n个点的最大值即 a[i]~a[i+n-1];(i+n-1<=n)

 

            

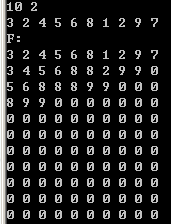
f[1][0]=a[1]=3;	f[2][0]=a[2]=2;	f[3][0]=a[3]=4;	f[4][0]=a[4]=5;	f[5][0]=a[5]=6;	f[6][0]=a[6]=8;	f[7][0]=a[7]=1;	f[8][0]=2;	f[9][0]=9;	f[10][0]=7;
f[1][1]=max(f[1][0],f[2][0])=3	f[2][1]=max(f[2][0],f[3][0])=4	f[3][1]=max(f[3][0],f[4][0])=5	f[4][1]=max(f[4][0],f[5][0])=6	f[5][1]=max(f[5][0],f[6][0])=8	f[6][1]=8	f[7][1]=2	f[8][1]=9	f[9][1]=9
f[1][2]=max(f[1][1],f[3][1])=4	f[2][2]=max(f[2][1],f[4][1])=6	f[3][2]=max(f[3][1],f[5][1])=8	f[4][2]=max(f[4][1],f[6][1])=8	f[5][2]=max(f[5][1],f[7][1])= 8	f[6][2]=9	f[7][2]=9
f[1][3]=max(f[1][2],f[5][2])=8	f[2][3]=max(f[2][2],f[6][2])=9	f[3][3]=max(f[3][2],f[7][2])=9

 

ST:

void st(){  //时间复杂度O(nlogn)

int k=log(n)/log(2);//求深度
for(int i=1;i<=n;i++)f[i][0]=a[i];//初始化
for(int j=1;j<=k;j++)
for(int i=1;i+(1<<j)-1<=n;i++)//长度为2^j的区间[i,i+2^j-1] ，所以当i+(1<<j)-1>n时循环停止
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}

RMQ(Range Minimum/Maximum Query)问题 //区间最值查询:

int qwt(int L,int R){//时间复杂度O(1)    

int k=log(R-L+1)/log(2);//2^k<=R-L+1,但2*2^k>R-L+1
return max(f[L][k],f[R-(1<<k)+1][k]);//L+2^k-1<=R,R-2^k+1>=L,所以区间[L,L+2^k-1]和[,R-2^k+1,R]是正好相切或者有部分重合，也就是说两个区间是无缝衔接的，这样求两个区间最值的最值就是所求答案。
}

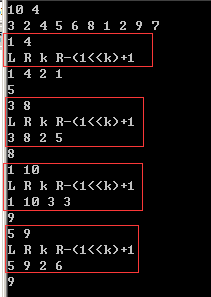
L=1，R=4时 求的是  max(f[1][2],f[1][2]) 即区间【1,4】【1,4】

L=3，R=8时 求的是  max(f[3][2],f[6][2])即区间【3,6】【5，8】，两个区间中5,6是重合的

L=1，R=10时 求的是  max(f[1][3],f[3][10])即区间【1,8】【3，10】，两个区间中3~8是重合的

#include<iostream>
#include<cmath>
#include<cstdio>
using namespace std;
const int maxn=100100;
int n,m;
int f[maxn][20],a[maxn];
void st(){
    int k=log(n)/log(2);
    for(int i=1;i<=n;i++)f[i][0]=a[i];
    for(int j=1;j<=k;j++)
        for(int i=1;i+(1<<j)-1<=n;i++)//长度为2^j的区间[i,i+2^j-1] 
            f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
int qwt(int L,int R){
    int k=log(R-L+1)/log(2);
    return max(f[L][k],f[R-(1<<k)+1][k]);
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    st();
    for(int i=1;i<=m;i++){
        int x,y;
        scanf("%d%d",&x,&y);
        printf("%d
",qwt(x,y));
    }    
    return 0;
}

 注意：当输入输出数据的规模达到10的6次方时，就需要用scanf和pritf输入输出。此时用cin和cout是绝对会超时的。