上一篇文章我们介绍了使用逻辑回归来处理分类问题,本文我们讲一个更强大的分类模型。本文依旧侧重代码实践,你会发现我们解决问题的手段越来越丰富,问题处理起来越来越简单。
支持向量机(Support Vector Machine, SVM)是最受欢迎的机器学习模型之一。它特别适合处理中小型复杂数据集的分类任务。
一、什么是支持向量机
SMV在众多实例中寻找一个最优的决策边界,这个边界上的实例叫做支持向量,它们“支持”(支撑)分离开超平面,所以它叫支持向量机。
那么我们如何保证我们得到的决策边界是最优的呢?
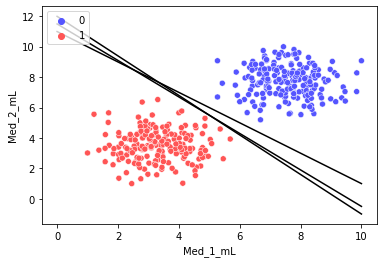
如上图,三条黑色直线都可以完美分割数据集。由此可知,我们仅用单一直线可以得到无数个解。那么,其中怎样的直线是最优的呢?
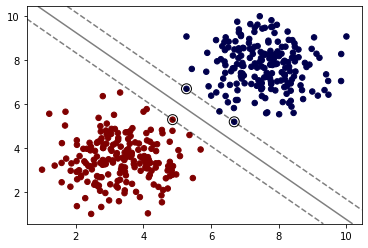
如上图,我们计算直线到分割实例的距离,使得我们的直线与数据集的距离尽可能的远,那么我们就可以得到唯一的解。最大化上图虚线之间的距离就是我们的目标。而上图中重点圈出的实例就叫做支持向量。
这就是支持向量机。
二、从代码中映射理论
2.1 导入数据集
添加引用:
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
导入数据集(大家不用在意这个域名):
df = pd.read_csv('https://blog.caiyongji.com/assets/mouse_viral_study.csv')
df.head()
| Med_1_mL | Med_2_mL | Virus Present | |
|---|---|---|---|
| 0 | 6.50823 | 8.58253 | 0 |
| 1 | 4.12612 | 3.07346 | 1 |
| 2 | 6.42787 | 6.36976 | 0 |
| 3 | 3.67295 | 4.90522 | 1 |
| 4 | 1.58032 | 2.44056 | 1 |
该数据集模拟了一项医学研究,对感染病毒的小白鼠使用不同剂量的两种药物,观察两周后小白鼠是否感染病毒。
- 特征: 1. 药物Med_1_mL 药物Med_2_mL
- 标签:是否感染病毒(1感染/0不感染)
2.2 观察数据
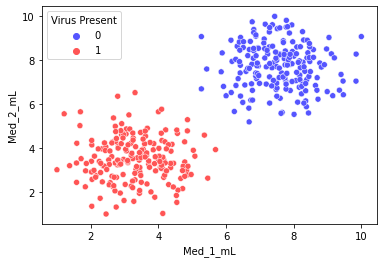
sns.scatterplot(x='Med_1_mL',y='Med_2_mL',hue='Virus Present',data=df)
我们用seaborn绘制两种药物在不同剂量特征对应感染结果的散点图。
sns.pairplot(df,hue='Virus Present')
我们通过pairplot方法绘制特征两两之间的对应关系。
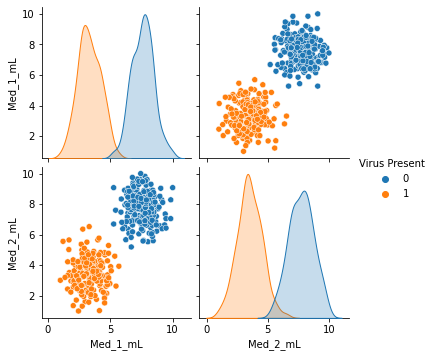
我们可以做出大概的判断,当加大药物剂量可使小白鼠避免被感染。
2.3 使用SVM训练数据集
#SVC: Supprt Vector Classifier支持向量分类器
from sklearn.svm import SVC
#准备数据
y = df['Virus Present']
X = df.drop('Virus Present',axis=1)
#定义模型
model = SVC(kernel='linear', C=1000)
#训练模型
model.fit(X, y)
# 绘制图像
# 定义绘制SVM边界方法
def plot_svm_boundary(model,X,y):
X = X.values
y = y.values
# Scatter Plot
plt.scatter(X[:, 0], X[:, 1], c=y, s=30,cmap='coolwarm')
# plot the decision function
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# create grid to evaluate model
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model.decision_function(xy).reshape(XX.shape)
# plot decision boundary and margins
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
# plot support vectors
ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=100,
linewidth=1, facecolors='none', edgecolors='k')
plt.show()
plot_svm_boundary(model,X,y)
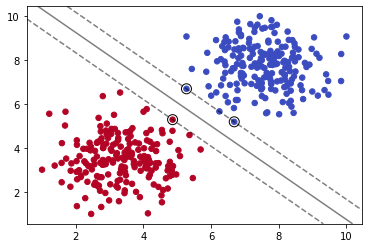
我们导入sklearn下的SVC(Supprt Vector Classifier)分类器,它是SVM的一种实现。
2.4 SVC参数C
SVC方法参数C代表L2正则化参数,正则化的强度与C的值城反比,即C值越大正则化强度越弱,其必须严格为正。
model = SVC(kernel='linear', C=0.05)
model.fit(X, y)
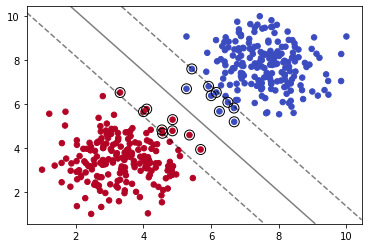
plot_svm_boundary(model,X,y)
我们减少C的值,可以看到模型拟合数据的程度减弱。
2.5 核技巧
SVC方法的kernel参数可取值{'linear', 'poly', 'rbf', 'sigmoid', 'precomputed'}。像前文中所使用的那样,我们可以使kernel='linear'进行线性分类。那么如果我们像进行非线性分类呢?
2.5.1 多项式内核
多项式内核kernel='poly'的原理简单来说就是,用单一特征生成多特征来拟合曲线。比如我们拓展X到y的对应关系如下:
| X | X^2 | X^3 | y | |
|---|---|---|---|---|
| 0 | 6.50823 | 6.50823**2 | 6.50823**3 | 0 |
| 1 | 4.12612 | 4.12612**2 | 4.12612**3 | 1 |
| 2 | 6.42787 | 6.42787**2 | 6.42787**3 | 0 |
| 3 | 3.67295 | 3.67295**2 | 3.67295**3 | 1 |
| 4 | 1.58032 | 1.58032**2 | 1.58032**3 | 1 |
这样我们就可以用曲线来拟合数据集。
model = SVC(kernel='poly', C=0.05,degree=5)
model.fit(X, y)
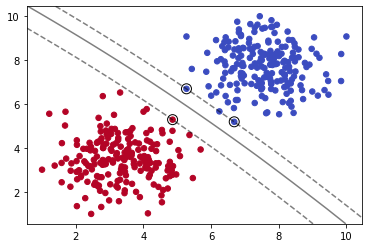
plot_svm_boundary(model,X,y)
我们使用多项式内核,并通过degree=5设置多项式的最高次数为5。我们可以看出分割出现了一定的弧度。
2.5.2 高斯RBF内核
SVC方法默认内核为高斯RBF,即Radial Basis Function(径向基函数)。这时我们需要引入gamma参数来控制钟形函数的形状。增加gamma值会使钟形曲线变得更窄,因此每个实例影响的范围变小,决策边界更不规则。减小gamma值会使钟形曲线变得更宽,因此每个实例的影响范围变大,决策边界更平坦。
model = SVC(kernel='rbf', C=1,gamma=0.01)
model.fit(X, y)
plot_svm_boundary(model,X,y)

2.6 调参技巧:网格搜索
from sklearn.model_selection import GridSearchCV
svm = SVC()
param_grid = {'C':[0.01,0.1,1],'kernel':['rbf','poly','linear','sigmoid'],'gamma':[0.01,0.1,1]}
grid = GridSearchCV(svm,param_grid)
grid.fit(X,y)
print("grid.best_params_ = ",grid.best_params_,", grid.best_score_ =" ,grid.best_score_)
我们可以通过GridSearchCV方法来遍历超参数的各种可能性来寻求最优超参数。这是通过算力碾压的方式暴力调参的手段。当然,在分析问题阶段,我们必须限定了各参数的可选范围才能应用此方法。
因为数据集太简单,我们在遍历第一种可能性时就已经得到100%的准确率了,输出如下:
grid.best_params_ = {'C': 0.01, 'gamma': 0.01, 'kernel': 'rbf'} , grid.best_score_ = 1.0
总结
当我们处理线性可分的数据集时,可以使用SVC(kernel='linear')方法来训练数据,当然我们也可以使用更快的方法LinearSVC来训练数据,特别是当训练集特别大或特征非常多的时候。
当我们处理非线性SVM分类时,可以使用高斯RBF内核,多项式内核,sigmoid内核来进行非线性模型的的拟合。当然我们也可以通过GridSearchCV寻找最优参数。