凸包算法(Graham扫描法)详解
先说下基础知识,不然不好理解后面的东西
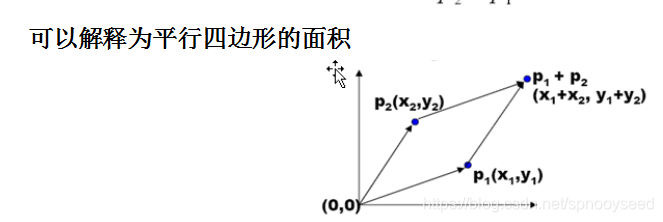
两向量的X乘p1(x1,y1),p2(x2,y2)
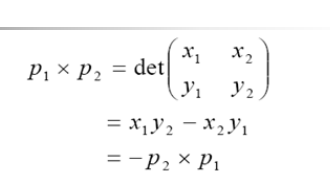
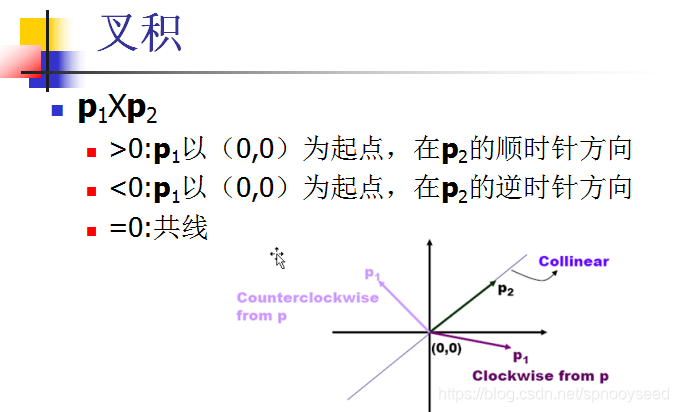
p1Xp2如果小于零则说明 p1在p2的逆时针方向
如果大于零则说明 p1在p2的顺时针方向
struct node{
double x,y;
node friend operator -(node a,node b)//对减法符号进行重载
{
return {a.x-b.x,a.y-b.y};
}
}p[10000],s[10000];
double X(node a,node b){
return a.x*b.y-a.y*b.x;
}
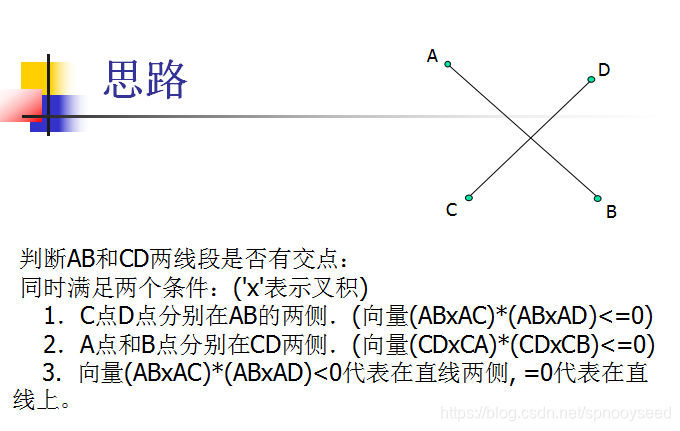
这个方法很有用处。比如判断一个点是否在一条线段的左边还是右边,可以用X乘来判断,或者判断两条线段是否相交
接着说说凸包 Graham扫描法
1.在平面上一些散乱的点,首先 找找到这些点中处于最左下方的点
for(int i=1;i<=N;i++)
cin>>p[i].x>>p[i].y;
int k=1;
for(int i=2;i<=N;i++)
{
if(p[i].y<p[k].y||(p[k].y==p[i].y&&p[i].x<p[k].x))
k=i;
}
swap(p[1],p[k]);
2.对这些点进行排序。把按照极角(polar angle)从小到大排序(以 p1为极点),极角相同的点按照到的距离从小到大排序。
int cmp(node a,node b)
{
double x=X(a-p[1],b-p[1]);//以p[1]为极点,通过X乘来判断
if(x>0) return 1;//让a处于b的顺时针
if(x==0&&dis(a,p[1])<dis(b,p[1]))return 1;//角度相同看距离
return 0;
}
sort(p+2,p+N+1,cmp);
3.再开一个结构体数组s 来储存凸包最外围的点,也就是结果,这个有点容易让人搞迷。
遍历剩下的点,while循环把发现不是凸包顶点的点移除出去,因为当逆时针遍历凸包时,我们应该在每个顶点向左转。因此当while循环发现在一个顶点处没有向左转时,就把该顶点移除出去。
至于如何判断向左向右则是根据叉积来判断,前面我们已经解决过这个问题了
double multi(node a,node b,node c)
{
return X(b-a,c-a);
}
s[1]=p[1];
s[2]=p[2];
int t=2;
for(int i=3;i<=N;i++)
{
// 发现在栈里边一个顶点处没有向左转时,就把该顶点移除出去
while(t>=2&&multi(s[t-1],s[t],p[i])<=0) t--;
s[++t]=p[i];
}
这个是求凸包的周长的
hdu1392 http://acm.hdu.edu.cn/showproblem.php?pid=1392
算是模板题吧
#include<bits/stdc++.h>
using namespace std;
struct point{
double x,y;
point friend operator -(point a,point b)
{return {a.x-b.x,a.y-b.y};}
}p[105],s[105];
double dis(point a,point b)
{
point c=a-b;
return sqrt(c.x*c.x+c.y*c.y);
}
double X(point a,point b)
{
return a.x*b.y-a.y*b.x;
}
int cmp(point a,point b)
{
double x=X(a-p[1],b-p[1]);
if(x>0) return 1;
if(x==0&&dis(a,p[1])<dis(b,p[1])) return 1;
return 0;
}
double multi(point p1,point p2,point p3)
{
return X(p2-p1,p3-p1);
}
int main()
{
int N;
while(scanf("%d",&N),N)
{
for(int i=1;i<=N;i++) cin>>p[i].x>>p[i].y;
if(N==1)
{
printf("0.00
");
continue;
}
else if(N==2)
{
printf("%.2lf
",dis(p[1],p[2]));
continue;
}
int k=1;
for(int i=2;i<=N;i++)
if(p[i].y<p[k].y||(p[i].y==p[k].y&&p[i].x<p[k].x))k=i;
swap(p[1],p[k]);
sort(p+2,p+1+N,cmp);
s[1]=p[1];
s[2]=p[2];
int t=2;
for(int i=3;i<=N;i++)
{
while(t>=2&&multi(s[t-1],s[t],p[i])<=0) t--;
s[++t]=p[i];
}
double sum=0;
for(int i=1;i<t;i++)
{
sum+=dis(s[i],s[i+1]);
}
printf("%.2lf
",sum+dis(s[1],s[t]));
}
return 0;
}
emmm 再来个求任意多边形的面积
struct Point {
double x, y;
};
//计算任意多边形的面积,顶点按照顺时针或者逆时针方向排列
double polygon_area(Point *p, int n)
{
if(n < 3) return 0;
double sum = 0;
p[n + 1] = p[1];
for(int i = 1; i <= n; i++)
sum += p[i].x * p[i + 1].y - p[i].y * p[i + 1].x;//可以理解为不管这个多边形在哪,都以原点为分割点,就算原点在外面也可以算出,因为有正负可以抵消掉多余的
sum = fabs(sum / 2.0);
return sum;
}
再来个求面积均匀的多边形重心
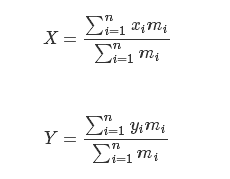
需要把多边形以p[0]为分界点 分成n-2个三角形,求出这些三角形的重心(i,j),乘以该三角形的面积,如上图公式
#include<bits/stdc++.h>
using namespace std;
struct node{
double x,y;
node friend operator -(node a,node b)
{
return {a.x-b.x,a.y-b.y};
}
double friend operator *(node a,node b)//对*进行重载 node*node 相当于X乘
{
return a.x*b.y-a.y*b.x;
}
}a[1000010];
int main()
{
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i].x>>a[i].y;
double S=0,X=0,Y=0;
for(int i=2;i<n;i++)
{
double x=(a[i]-a[1])*(a[i+1]-a[1]);//这个乘和下面的不一样,这时X乘,求出三角形面积
X+=(a[1].x+a[i].x+a[i+1].x)*x;//重心(没除以3)乘以面积
Y+=(a[1].y+a[i].y+a[i+1].y)*x;
S+=x;
}
printf("%.2lf %.2lf
",X/S/(double)3,Y/S/(double)3);//除以3为重心
}
return 0;
}