博弈论
1.算法分析
1.1 基本概念
1.1.1 必胜
先手必胜状态:可以走到某一个必败状态
先手必败状态:走不到任何一个必败状态
1.1.2 ICG
公平组合游戏ICG
若一个游戏满足:
1. 由两名玩家交替行动
2. 在游戏进程的任意时刻,可以执行的合法行动于轮到哪名玩家无关
3. 不能行动的玩家判负
1.1.3 nim游戏
nim游戏:
a1 ^ a2 ^ ... ^ an = 0, 先手必败
a1 ^ a2 ^ ... ^ an != 0, 先手必胜
证明:
① 0 ^ 0 ^ ... ^ 0 = 0
②a1 ^ a2 ^ ... ^ an = x != 0,一定可以通过某种操作(拿去ai里面的k个石子,k = ai - (ai - x))使得a1 ^ a2 ^ ... ^ an = 0
③a1 ^ a2 ^ ... ^ an = 0,无论怎么操作,最后a1 ^ a2 ^ ... ^ an = x != 0
因此,a1 ^ a2 ^ ... ^ an = 0, 先手必败;a1 ^ a2 ^ ... ^ an != 0, 先手必胜
1.1.4 有向图游戏
定义:
给定一个有向无环图,图中有唯一的起点,在起点上放有一个棋子。两名玩家交替把这个棋子沿着有向边进行移动,每次可以移动一步,无法移动者判负。该游戏被称为有向图游戏。具体方法是,把每个局面看成图中的一个节点,并且从每个局面沿着合法行动能够到达的下一个局面连有向边
1.1.5 Mex运算
Mex运算
设S表示一个非负整数集合,定义Mex(S)为求出不属于集合S的最小非负整数的运算,即: Mex(S) = min(x), x属于自然数,且x不属于S
1.1.6 SG函数
SG函数
在有向图游戏中,对于每个节点x,设从x出发公用k条有向边,分别到达节点y1,y2,...,yk。定义SG(x)为x的后继节点y1,y2,...,yk的SG函数值构成的集合再执行mex(s)运算的结果,即:SG(x)=mex({SG(y1}, SG(y2), ..., SG(yk))
特别的,整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值,即SG(G)=SG(s)
定理
有向图游戏的某个局面必胜,当且仅当该局面对应节点的SG函数值大于0
有向图游戏的某个局面必败,当且仅当该局面对应节点的SG函数值等于0
2. 典型例题
2.1 nim游戏
2.1.1 普通nim游戏
思路: 普通nim游戏直接套用结论,全部异或,是0必败,非0必胜
acwing891Nim游戏
给定n堆石子,两位玩家轮流操作,每次操作可以从任意一堆石子中拿走任意数量的石子(可以拿完,但不能不拿),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数n。
第二行包含n个数字,其中第 i 个数字表示第 i 堆石子的数量。
输出格式
如果先手方必胜,则输出“Yes”。
否则,输出“No”。
数据范围
1≤n≤105,
1≤每堆石子数≤109
输入样例:
2
2 3
输出样例:
Yes
/*
a1 ^ a2 ^ ... ^ an = 0, 先手必败;a1 ^ a2 ^ ... ^ an != 0, 先手必胜
*/
#include<bits/stdc++.h>
using namespace std;
int const N = 1e5 + 10;
int a[N], n;
int main()
{
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
cin >> n;
int res = 0;
for (int i = 1; i <= n; ++i)
{
scanf("%d", &a[i]);
res ^= a[i];
}
if (!res) printf("No
");
else printf("Yes
");
return 0;
}
acwing229新nim游戏
一共k堆火柴,每堆n个。在第一个回合中,第一个游戏者可以直接拿走若干个整堆的火柴。可以一堆都不拿,但不可以全部拿走。第二回合也一样,第二个游戏者也有这样一次机会。从第三个回合(又轮到第一个游戏者)开始,规则和Nim游戏一样。问是否先手必胜,如果可以获胜的话,还要让第一回合拿的火柴总数尽量小。1<=k<=100, 1<=n<=1e9
/* 仔细思考就知道只需要第一个人拿完以后,剩下的所以堆任选几个异或不会出现0即可
所以只需要先排序,然后从小到大拿,每次拿完插入线性基,判断是否插入成功即可 */
#include <bits/stdc++.h>
using namespace std;
int const N = 1e2 + 10;
int a[N], n, b[32], flg;
bool insert(int x) {
for (int i = 31; i >= 0; --i) {
if (x & (1ll << i))
if (!b[i]) {
b[i] = x;
return true;
}
else x ^= b[i];
}
flg = 0;
return false;
}
int main()
{
cin >> n;
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
sort(a + 1, a + n + 1);
reverse(a + 1, a + 1 + n);
long long res = 0;
for (int i = 1; i <= n; ++i) {
if (!insert(a[i])) res += a[i];
}
cout << res << endl;
return 0;
}
2.1.2 台阶nim游戏
思路: 台阶nim游戏可以转换为nim游戏,对奇数位直接套用结论,全部异或,是0必败,非0必胜
acwing892台阶-nim游戏
现在,有一个n级台阶的楼梯,每级台阶上都有若干个石子,其中第ii级台阶上有ai个石子(i≥1)。
两位玩家轮流操作,每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中(不能不拿)。
已经拿到地面上的石子不能再拿,最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数n。
第二行包含n个整数,其中第i个整数表示第i级台阶上的石子数ai。
输出格式
如果先手方必胜,则输出“Yes”。
否则,输出“No”。
数据范围
1≤n≤105,
1≤ai≤109
输入样例:
3
2 1 3
输出样例:
Yes
/*
本题可以把奇数位台阶的石子转化为普通的nim游戏,然后套用结论即可
*/
#include<bits/stdc++.h>
using namespace std;
int const N = 1e5 + 10;
int a[N], n;
int main()
{
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
cin >> n;
int res = 0;
for (int i = 1; i <= n; ++i)
{
scanf("%d", &a[i]);
if (i & 1) res ^= a[i];
}
if (!res) printf("No
");
else printf("Yes
");
return 0;
}
luoguP2575高手过招
对于一个棋子,能将它向右移动一格,如果右边有棋子,则向右跳到第一个空格,如果右边没有空格,则不能移动这个棋子,如果所有棋子都不能移动,那么将输掉这场比赛。
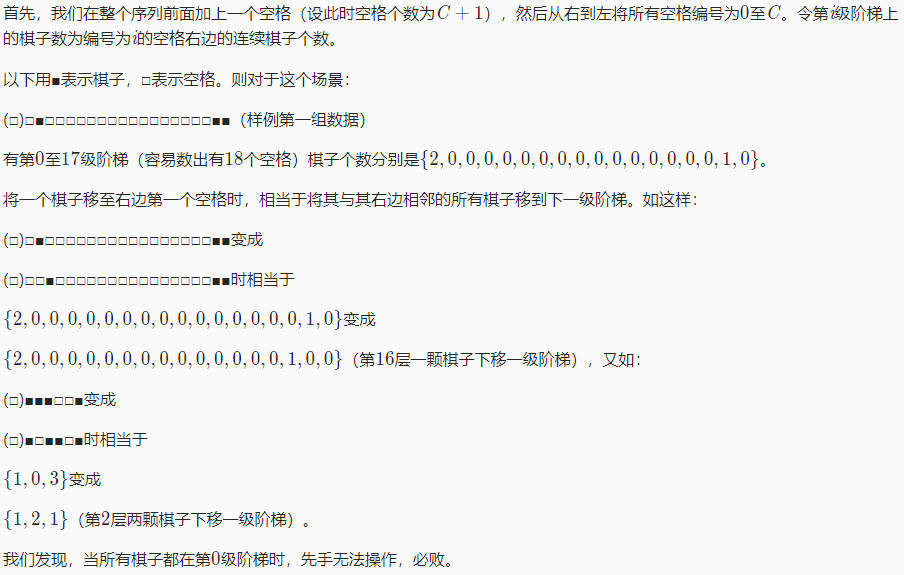
/* 从每一行的角度来看,每一行相当于一个台阶nim游戏,
然后从整个棋盘的角度来看,每行都相当于一个有向图游戏,因此只需要把每行的结果做一个异或和即可
现在分析下,为什么每一行都是一个台阶nim游戏,我们把每个空格拿出来看,在最左边开头插入一个空格,每个空格右边连续的黑色棋子个数都认为是台阶上的棋子数目
最右边那个空格右边的棋子数就是地面上的棋子
然后每次移动一个棋子就相当于把台阶上任意棋子拿到下一个台阶上去
那就是台阶nim,对奇数台阶做个异或和即可 */
#include <bits/stdc++.h>
using namespace std;
int const N = 25;
int t, a[N], n, row, vis[N];
int main()
{
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
cin >> t;
while (t--)
{
/* code */
int ans = 0;
scanf("%d", &row);
while(row--) {
scanf("%d", &n);
memset(vis, 0, sizeof vis);
for (int i = 1, t; i <= n; ++i) {
scanf("%d", &t);
vis[t] = 1;
}
int row_xor = 0, cnt = 0, tmp = 0;
for (int i = 20; i >= 0; --i) {
if (!vis[i]) {
if ((cnt++) & 1) row_xor ^= tmp;
tmp = 0;
}
else tmp++;
}
ans ^= row_xor;
}
if (!ans) printf("NO
");
else printf("YES
");
}
return 0;
}
acwing236格鲁吉亚和鲍勃
有一排方格(1*n),一次编号为1,2,3,...,100000,现在在网格上防止n个棋子。每次可以选择一个棋子,向左移动到左边的空格(但是不能移动到前一个棋子的左侧),一旦没有棋子可以移动就输了。先手必胜,输出Georgia will win;先手必败输出Bob will win,不确定输出Not sure。测试样例T<=20,棋子数吗n<=1000.
/*
把每个棋子右边的空格当作台阶上的石子,那么最右边的那颗棋子右边的空格数目,相当于地面上的石子;次右边的棋子右边的空格数目,相当于第一级台阶上的棋子数目;...;同时还需要在第0格补充一个位置,然后台阶nim即可
*/
#include <bits/stdc++.h>
using namespace std;
int const N = 1e3 + 10;
int a[N], n, t, sum[N];
int main()
{
cin >> t;
while (t--)
{
cin >> n;
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
sort(a + 1, a + n + 1);
int res = 0;
int pos = 2;
if (n & 1) pos = 1;
for (int i = n; i >= pos; i -= 2) {
res ^= (a[i] - a[i - 1] - 1);
}
if (res) printf("Georgia will win
");
else printf("Bob will win
");
}
return 0;
}
2.1.3 集合nim游戏
思路: 集合nim游戏的每个初值均为一张有向图的起点,套用SG函数即可
acwing893.集合nim游戏
给定nn堆石子以及一个由k个不同正整数构成的数字集合S。
现在有两位玩家轮流操作,每次操作可以从任意一堆石子中拿取石子,每次拿取的石子数量必须包含于集合S,最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数k,表示数字集合S中数字的个数。
第二行包含k个整数,其中第i个整数表示数字集合S中的第i个数si。
第三行包含整数n。
第四行包含n个整数,其中第i个整数表示第i堆石子的数量hi。
输出格式
如果先手方必胜,则输出“Yes”。
否则,输出“No”。
数据范围
1≤n,k≤100,
1≤si,hi≤10000
输入样例:
2
2 5
3
2 4 7
输出样例:
Yes
/*
由sg函数的性质可以知道,有向图游戏中,sg(G1)^sg(G2)^...^sg(Gn)=0,先手必败;否则,先手必胜
求sg函数按照他的定义可以使用记忆化搜索来得到
*/
#include<bits/stdc++.h>
using namespace std;
int n, k;
int const N = 1e2 + 10, M = 1e4 + 10;
int s[N];
int f[M];
// 记忆化搜索求sg函数
int sg(int x)
{
if (f[x] != 0) return f[x];
unordered_set<int> S;
for (int i = 1; i <= n; ++i)
{
int sum = s[i];
if (x >= sum) S.insert(sg(x - sum));
}
for (int i = 0; ; i++)
if (!S.count(i)) return f[x] = i;
}
int main()
{
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
cin >> n;
for (int i = 1; i <= n; ++i) cin >> s[i];
cin >> k;
int res = 0; // 记录sg(G)
for (int i = 1; i <= k; ++i)
{
int t;
cin >> t;
res ^= sg(t);
}
if (!res) cout << "No
";
else cout << "Yes
";
return 0;
}
2.1.4 拆分nim游戏
思路: 拆分nim游戏每次把一个点拆分的子状态都是多个有向图,比如把x点可以拆分成(x1, y1), (x2,y2),...,(xn,yn),其中的(xi, yi)是两张起点为xi和yi的有向图
acwing894 拆分-nim游戏
给定n堆石子,两位玩家轮流操作,每次操作可以取走其中的一堆石子,然后放入两堆规模更小的石子(新堆规模可以为0,且两个新堆的石子总数可以大于取走的那堆石子数),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
输入格式
第一行包含整数n。
第二行包含n个整数,其中第i个整数表示第i堆石子的数量ai。
输出格式
如果先手方必胜,则输出“Yes”。
否则,输出“No”。
数据范围
1≤n,ai≤100
输入样例:
2
2 3
输出样例:
Yes
/*
u能够到达的局面为(i, j), i<u,j<u
而sg[(b1, b2)] = sg(b1) ^ sg(b2)
因此使用有向图游戏处理即可
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 110;
int n;
int f[N];
int sg(int x)
{
if (f[x] != -1) return f[x];
unordered_set<int> S;
for (int i = 0; i < x; i ++ )
for (int j = 0; j <= i; j ++ )
S.insert(sg(i) ^ sg(j));
for (int i = 0;; i ++ )
if (!S.count(i))
return f[x] = i;
}
int main()
{
cin >> n;
memset(f, -1, sizeof f);
int res = 0;
while (n -- )
{
int x;
cin >> x;
res ^= sg(x);
}
if (res) puts("Yes");
else puts("No");
return 0;
}
2.2 DAG上dfs
luogu p1290 欧几里得游戏
给定两个数m和n,从其中较大的一个数,减去较小的数的正整数倍,先得到0的人获胜
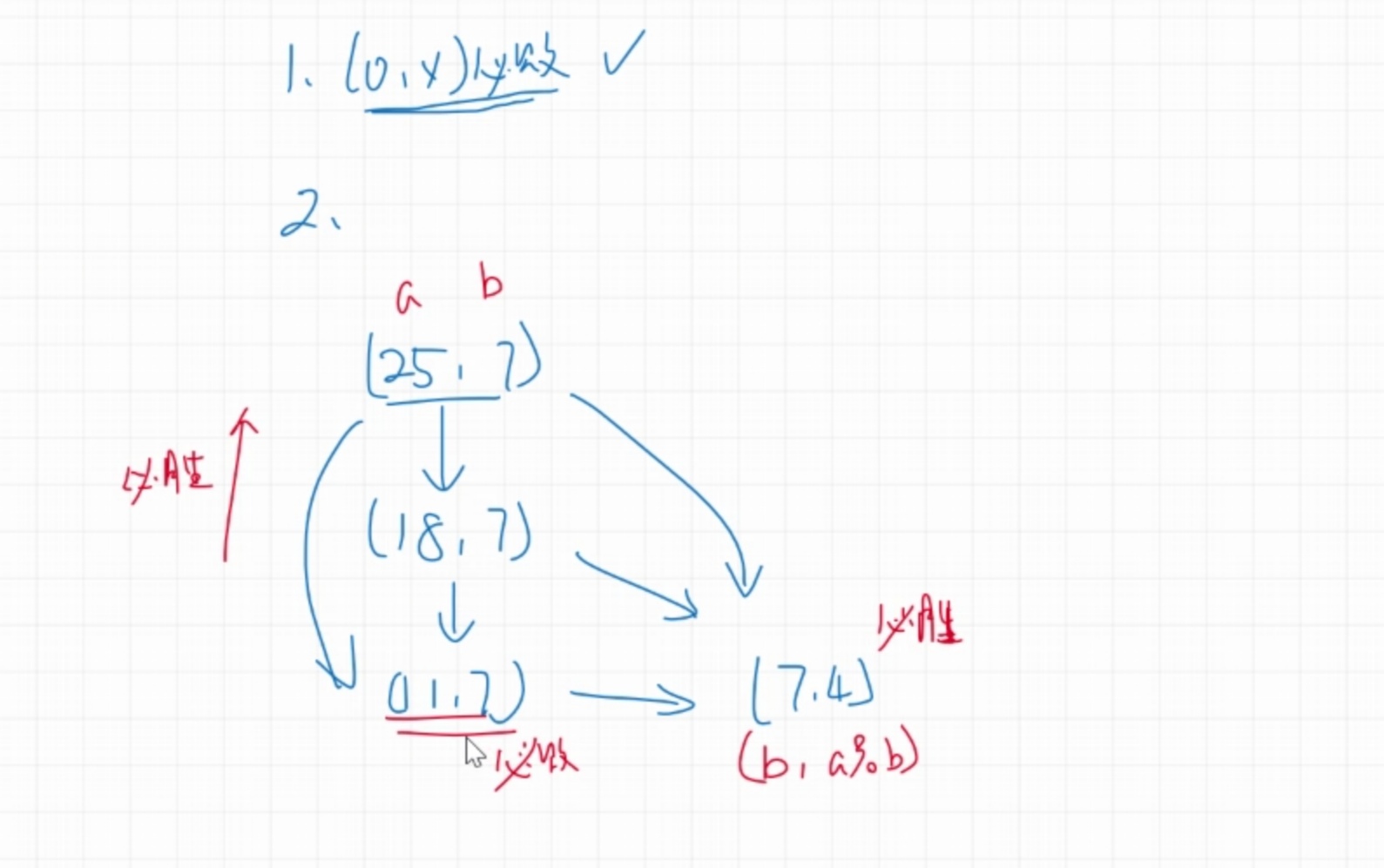
/* 如果能到必败态,那么这个状态一定是必胜态;如果不能到必败态,但是a>b,那么这个状态一定是必胜态;
如果b==0,那么这个状态是必败态 */
#include <bits/stdc++.h>
using namespace std;
int c, a, b;
bool dfs(int a, int b) {
if (a < b) swap(a, b);
if (b == 0) return 0;
if (dfs(b, a % b) == 0 || a > b * 2) return 1;
else return 0;
}
int main()
{
cin >> c;
while (c--)
{
scanf("%d %d", &a, &b);
if (b > a) swap(a, b);
if (dfs(a, b)) printf("Stan wins
");
else printf("Ollie wins
");
}
return 0;
}
2.3 有向图游戏
2.3.1 一般有向图游戏
acwing1319移棋子游戏
给定一个有 N 个节点的有向无环图,图中某些节点上有棋子,两名玩家交替移动棋子。
玩家每一步可将任意一颗棋子沿一条有向边移动到另一个点,无法移动者输掉游戏。
对于给定的图和棋子初始位置,双方都会采取最优的行动,询问先手必胜还是先手必败。
输入格式
第一行,三个整数 N,M,K,N 表示图中节点总数,M 表示图中边的条数,K 表示棋子的个数。
接下来 M 行,每行两个整数X,Y 表示有一条边从点 X 出发指向点 Y。
接下来一行, K 个空格间隔的整数,表示初始时,棋子所在的节点编号。
节点编号从 1 到 N。
输出格式
若先手胜,输出 win,否则输出 lose。
数据范围
1≤N≤2000,
1≤M≤6000,
1≤K≤N
输入样例:
6 8 4
2 1
2 4
1 4
1 5
4 5
1 3
3 5
3 6
1 2 4 6
输出样例:
win
/*
每个点都可以看成一个有向图的起点,所以k个起点就可以变成k张有向图
然后按照sg定理处理即可
*/
#include<bits/stdc++.h>
using namespace std;
int n, m, k;
int const N = 2e3 + 10, M = 6000 + 10;
int e[M], ne[M], h[N], idx;
int f[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// 记忆化搜索判定sg函数
int sg(int x)
{
if (f[x] != -1) return f[x];
unordered_set<int> S;
for (int i = h[x]; ~i; i = ne[i])
{
S.insert(sg(e[i]));
}
for (int i = 0; ; ++i)
if (!S.count(i)) return f[x] = i;
}
int main()
{
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
memset(h, -1, sizeof h);
cin >> n >> m >> k;
// 建图
for (int i = 1; i <= m; ++i)
{
int a, b;
scanf("%d %d", &a, &b);
add(a, b);
}
// 记忆化搜索求sg
memset(f, -1, sizeof f);
int res = 0;
for (int i = 0; i < k; ++i)
{
int t;
cin >> t;
res ^= sg(t);
}
// 1为胜,0为败
if (res) cout << "win
";
else cout << "lose
";
return 0;
}
acwing235魔法珠
freda和rainbow玩游戏,有n堆魔法珠,每次可以选择一堆魔法珠,该堆数目为p,使之变成m堆(每堆b1,b2,b3,...,bm,其中bi为p的约数,且bi < p, b1=1),然后选择这m堆中的一堆,使之消失。如果轮到某人操作时,每堆魔法珠个数均为1,那么他就输了。先手必胜输出,freda;先手必败,输出rainbow.
#include <bits/stdc++.h>
using namespace std;
int const N = 1010;
vector<int> fac[N];
int sg[N], n, a[N];
void init() {
for (int i = 1; i <= 1000; ++i) {
for (int j = 2; j * i <= 1000; ++j) {
fac[j * i].push_back(i);
}
}
}
int dfs(int u) {
if (sg[u] != -1) return sg[u];
if (u == 1) return sg[u] = 0;
int sum = 0;
for (int i = 0; i < fac[u].size(); ++i) {
sum = sum ^ dfs(fac[u][i]);
}
unordered_set<int> s;
for (int i = 0; i < fac[u].size(); ++i ) {
s.insert(sum ^ sg[fac[u][i]]);
}
for (int i = 0; ; ++i) {
if (!s.count(i)) return sg[u] = i;
}
}
int main()
{
init();
while(scanf("%d", &n) != EOF) {
memset(sg, -1, sizeof sg);
int res = 0;
for (int i = 1; i <= n; ++i) {
scanf ("%d", &a[i]);
res = res ^ dfs(a[i]);
}
if (res) printf("freda
");
else printf("rainbow
");
}
return 0;
}
2.3.2 非有向图游戏转化为有向图游戏
如果末状态为存在一堆石子数目为1,那么游戏结束,则不符合有向图游戏定义,需要进行转换;如果末状态为每一堆石子数目都为1,那么游戏结束,则为有向图游戏。
转换的方法就是改变末状态,使得出现石子数目为1的情况不会出现,把末状态变成每堆都为2(或3),即通过改变非有向图游戏的末状态来使得新的末状态符合有向图游戏的末状态的定义。
acwing219剪纸游戏
给定一张n * m的矩形网格之,每次可以沿着一行或一列的格线,把它剪成两部分,首先剪出1 * 1网格的玩家获胜。
2<=n,m<=200
/*
本题很直观的思路就是sg函数求解,但是如果把1*1的状态当成末状态,使得sg[1][1]=0,这样不符合有向图游戏的定义
因为有向图游戏是要走到走不动为止,而剪出1*1其实是还能继续走的,因为其他部分还能继续剪,所以不能直接套用有向图游戏
现在考虑如何把这个游戏变化成有向图游戏:
我们知道一旦建出1*x或x*1的长条,那么这个人一定必败,因此,在裁剪时我们避开剪出1*x的形状,把n*m的纸张剪成全部都为2*3,2*2的小方块,当成末状态,
这样就可以变化成有向图游戏了
*/
#include <bits/stdc++.h>
using namespace std;
int const N = 2e2 + 10;
int sg[N][N], n, m;
int dfs(int n, int m) {
if (n < m) swap(n, m);
if (sg[n][m] != -1) return sg[n][m];
unordered_set<int> s;
for (int i = 2; i <= n - i; ++i) {
s.insert(dfs(i, m) ^ dfs(n - i, m));
}
for (int i =2 ; i <= m - i; ++i) {
s.insert(dfs(n, i) ^ dfs(n , m - i));
}
for (int i = 0; ; ++i)
if (!s.count(i)) return sg[n][m] = i;
}
int main()
{
while (scanf("%d %d", &n, &m) != EOF)
{
if (n < m) swap(n, m);
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
sg[i][j] = -1;
if (dfs(n, m)) printf("WIN
");
else printf("LOSE
");
}
return 0;
}
2.4 思维博弈论
luogu P1199三国游戏
小涵和电脑比赛,有n个武将,每个武将i和其他武将j有一个默契值,每个武将都只能被选择一次。每次小涵选一个武将i后,电脑都会选择剩下所有武将中和i默契值最大的那个武将。最后得分为所有选择的武将中,默契值最大的那对武将的默契值。小涵先手,问小涵能否胜利,如果能够胜利输出1和最大的默契值;如果不能胜利,输出0
/* 对于武将i,当第一次出现武将i时,对应的最大默契值武将j一定会被电脑选走;
而i第二次出现时,可以直接选择和i配对的j', 那么就能选择到i的次大默契值。
而采用最优策略,一定能够保证人拿到的最大值更大:
因为一旦出现机器要拿到最大值的局面,人都可以拿走其中一半,使得这个最大值不出现;
而人出现最大值时可以直接结束游戏。 */
#include <bits/stdc++.h>
using namespace std;
int const N = 5e2 + 10;
int n, g[N][N];
int main()
{
cin >> n;
for (int i = 1; i <= n; ++i) {
for (int j = i + 1; j <= n; ++j)
{
scanf("%d", &g[i][j]);
g[j][i] = g[i][j];
}
}
int ans = 0;
for (int i = 1; i <= n; ++i) {
sort(g[i] + 1, g[i] + 1 + n);
ans = ans > g[i][n - 1] ? ans: g[i][n - 1];
}
cout << 1 << endl << ans << endl;
return 0;
}
luogu p4018Roy&October之取石子
现在有n个石子,每次可以取走p^k个石子,取完石子后石子个数变成0的那个人获胜。
/* 因为6的倍数都不是质数的幂次,所以如果是6的倍数那么先手必败,否则,先手必胜 */
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, t;
cin >> t;
while (t--)
{
cin >> n;
if (n % 6 == 0) printf("Roy wins!
");
else printf("October wins!
");
}
return 0;
}
luogu p4860 Roy&October之取石子II
现在有n个石子,每次可以取走p^k个石子(k为0或1),取完石子后石子个数变成0的那个人获胜。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n, t;
cin >> n;
while (n--)
{
cin >> t;
if (t % 4 == 0) printf("Roy wins!
");
else printf("October wins!
");
}
return 0;
}