给定一组数划平衡二叉树,结果是否唯一
单独的某个输入关键字序列如果没有删除,则自然结果唯一
如果没有限定关键字集合的次序,则结果不唯一,比如1、2、3、4
按1, 2, 3, 4输入次序构建的则右子树高度为2,根为2
按4, 3, 2, 1输入次序构建的则左子树高度为2,根为3
排序二叉树对于我们寻找无序序列中的元素的效率有了大大的提高。查找的最差情况是树的高度。这里就有问题了,将无序数列转化为
二叉排序树的时候,树的结构是非常依赖无序序列的顺序,这样会出现极端的情况。
【如图1】:

这样的一颗二叉排序树就是一颗比较极端的情况。我们在查找时候,效率依赖树的高度,所以不希望这样极端情况出现,而是希望元素比较均匀
的分布在根节点两端。
技术参考:fun4257.com/
问题提出:
能不能有一种方法,使得我们的二叉排序树不依赖无序序列的顺序,也能使得我们得到的二叉排序树是比较均匀的分布。
引入:
平衡二叉树(Self-Balancing Binary Search Tree 或 Height-Balanced Binary Search Tree),是一种特殊的二叉排序树,其中每一个结点的
左子树和右子树的高度差至多等于1.
这里的平衡从名字中可以看出,Height-Balanced是高度平衡。
它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1.
若将二叉树上的结点的平衡因子BF(Balance Factor)定义为该节点的左子树的深度减去它的右子树的深度,则平衡二叉树上所有结点的平衡因子只
可能是-1、0、1。否则就不是平衡二叉树。
上图图1中,就不是平衡二叉树。
以图1来看看各个结点的平衡因子。
【如下图2】:

技术参考:fun1404.com
如何构成平衡二叉树?






从转化为平衡二叉树的过程中可以提炼出转化的几个基本情况:
下图是在维基百科上摘录的:

可以看出调整的操作分两大类,前两个是一组,后两个是一组,每组之间是对称的。
前两个是对应上图1 2 中情况,
后两个是对应上图5 6 中情况。
分别以其中一种旋转为例,另一种对应的旋转对称。
单次左旋:对应上图1(左左)中情况
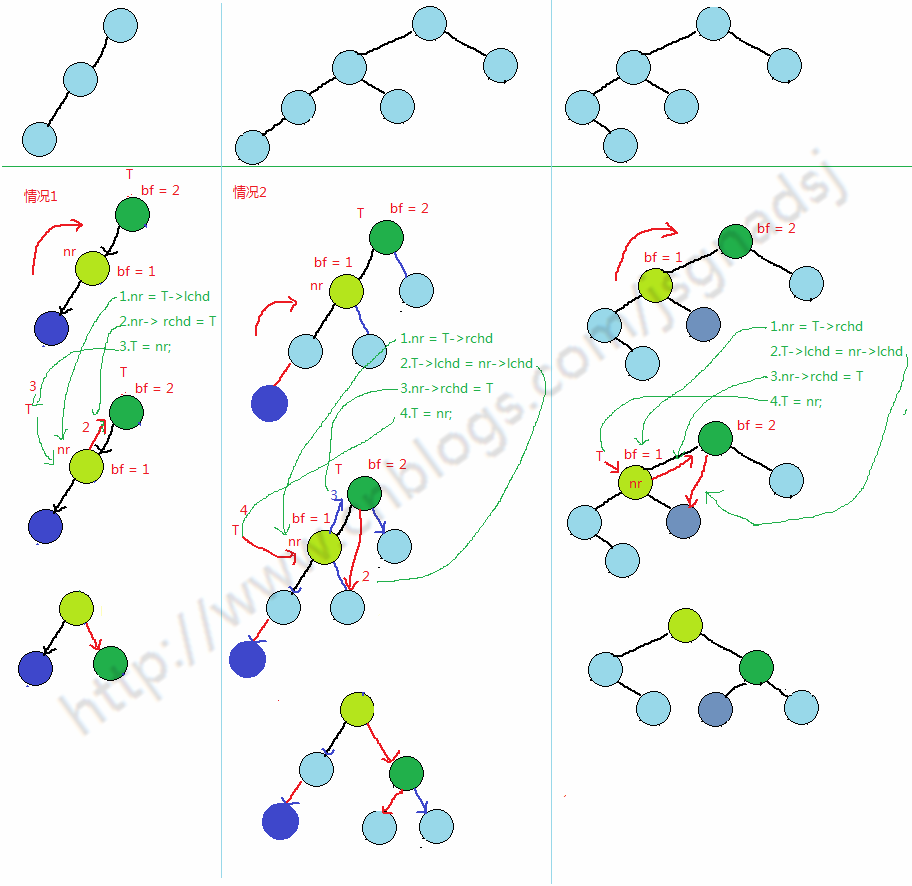
简单左右旋转代码:(只有一次)
//左边过高LL
TREE_NODE* SingleRotateWithLeft(TREE_NODE* root)
{
TREE_NODE* temp;
temp =root->left;
root->left = temp->right;
temp->right = root;
temp->height = Max(Height(temp->left),Height(temp->right))+1;
root->height = Max(Height(root->left),Height(root->right))+1;
return temp;
}
//右边高的时L
TREE_NODE* SingleRotateWithRight(TREE_NODE* root)
{
TREE_NODE* temp;
temp = root->right;
root->right = temp->left;
temp->left = root;
temp->height = Max(Height(temp->left),Height(temp->right))+1;
root->height = Max(Height(root->left),Height(root->right))+1;
return temp;
}两次旋转 对应图中3(左右)情况

需要旋转两次简单的左右旋转。基于上面代码就可以实现。
//左边过高LR
TREE_NODE* DoubleRotateWithLeft(TREE_NODE* root)
{
SingleRotateWithRight(root->left);
return SingleRotateWithLeft(root);
}
TREE_NODE* DoubleRotateWithRight(TREE_NODE* root)
{
SingleRotateWithLeft(root->right);
SingleRotateWithRight(root);
}为了方便,AVL引入了BF(平衡因子)来调整树。只要出现非平衡树就调整,把不平衡消除最小的情况。