学习资源:慕课网liyubobobo老师的《玩儿转数据结构》
目录
1、树的简介
-
树结构本身是一种天然的组织结构
- 计算机文件夹
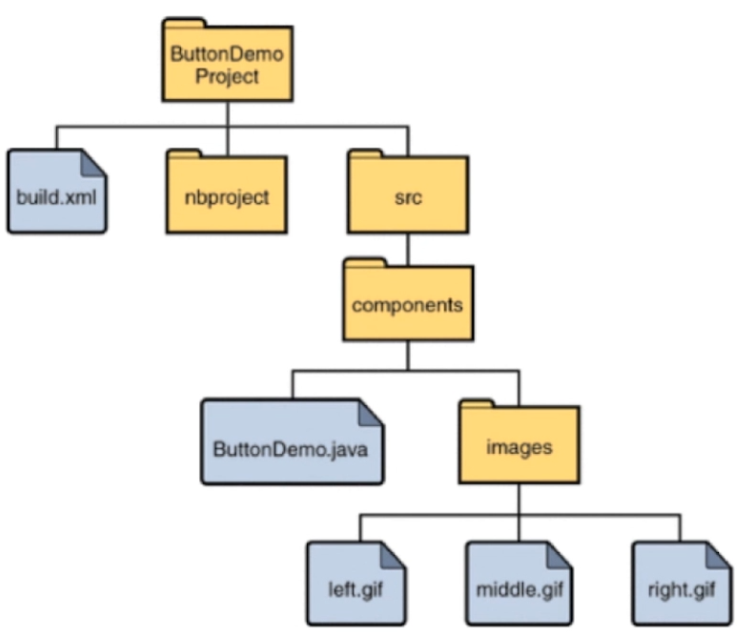
- 家谱
- 图书馆图书分类
- 公司职工
-
将数据使用树结构存储后,出奇的高效
2、树的分类
- 二分搜索树(Binary Search Tree)
- 平衡二叉树
- AVL
- 红黑树
- 堆
- 并查集
- 线段树
- Trie (字典树,前缀树)
3、二叉树简介
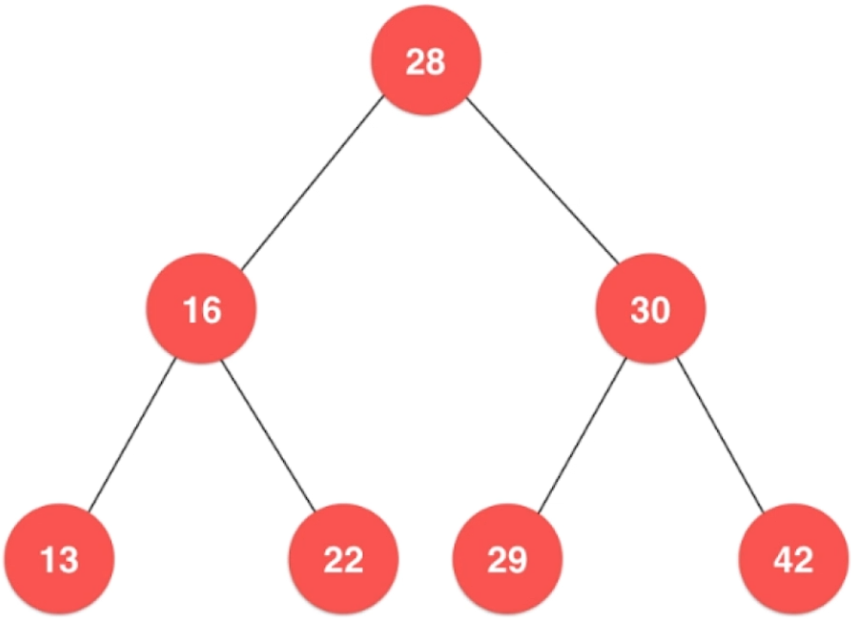
- 一个元素具有两个"分叉"
- 和链表一样,是动态的数据结构
class Node {
E e;
Node left; //左孩子
Node right; //右孩子
}
- 二叉树具有具有唯一根结点
- 二叉树每个结点最多有两个孩子
- 叶子结点:左右孩子都为空的结点
- 二叉树每个结点最多有一个父亲,根结点没有父结点
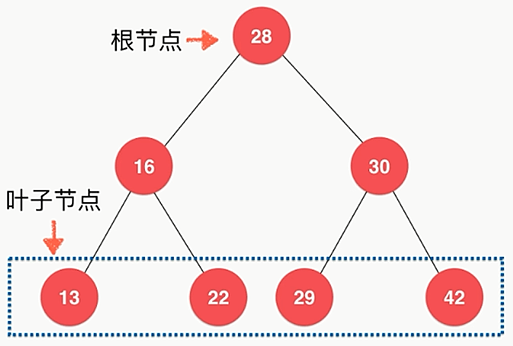
- 二叉树具有天然递归结构
- 每个结点的左子树也是二叉树
- 每个结点的右子树也是二叉树
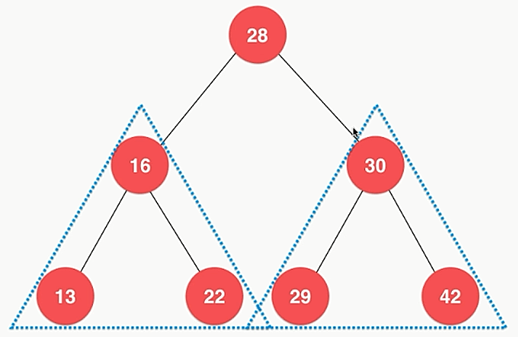
- 二叉树不一定是“满”的:一个结点也是二叉树;NULL也是二叉树;一个链表也可以看作是一个二叉树
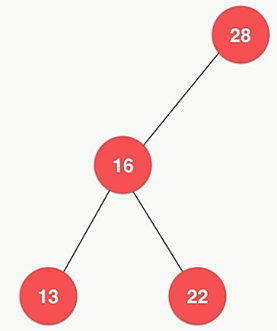
4、二分搜索树简介
- 二分搜索树也是一棵二叉树
- 二分搜索树的每个结点的值:
- 大于其左子树的所有结点的值
- 小于其右子树的所有结点的值
- 每一棵子树也是二分搜索树
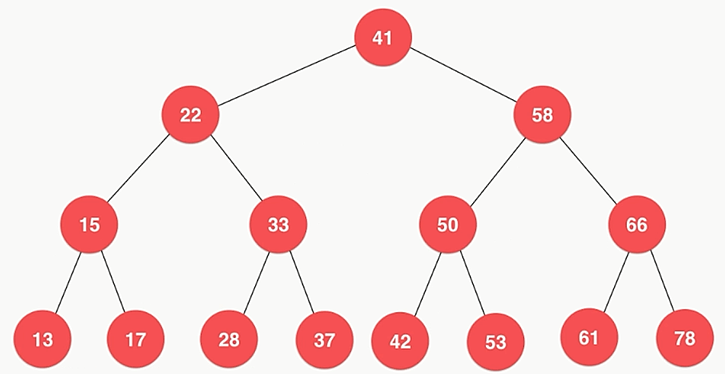
- 存储的元素必须有可比较性
- 二分搜索树不一定是一棵完全二叉树
5、可比较性的实现
6、二分搜索树的实现
6.1、插入元素
- 新元素,从根结点向下比较添加
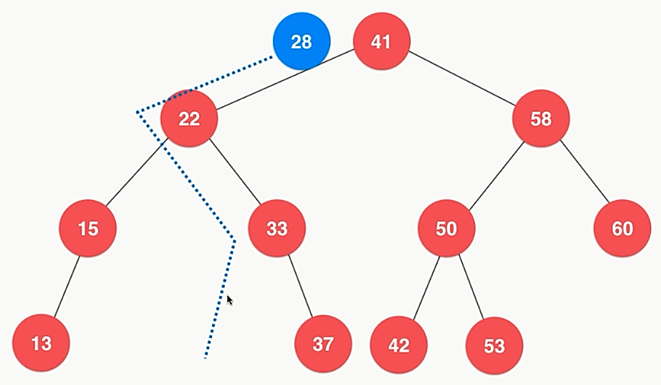
- 重复元素,不做处理
// 从二分搜索树中添加新的元素e
public void add(T t){
root = add(root, t);
}
private Node add(Node node, T t){
if(node == null){
size++;
return new Node(t);
}
if(t.compareTo(node.t) < 0){
node.left = add(node.left, t);
}
else if(t.compareTo(node.t) > 0){
node.right = add(node.right, t);
}
return node;
}
6.2、查询元素
public boolean contains(T t){
return contains(root, t);
}
private boolean contains(Node node, T t){
if(node == null){
return false;
}
if(t.compareTo(node.t) == 0){
return true;
}
else if(t.compareTo(node.t) > 0){
return contains(node.right, t);
}
else {
return contains(node.left, t);
}
}
6.3、遍历
- 遍历就是把所有结点都访问一遍
- 对于遍历操作,根结点的两棵子树都要顾及
6.3.1、递归遍历
前序遍历
先访问当前节点,再依次递归访问左右子树。
//前序遍历
public void preOrder(){
preOrder(root);
}
private void preOrder(Node node){
if(node == null){
return;
}
System.out.println(node.t);
preOrder(node.left);
preOrder(node.right);
}
中序遍历
先递归访问左子树,再访问自身,再递归访问右子树。中序遍历可实现二分搜索树元素的从小到大排序。
// 中序遍历
public void inOrder(){
inOrder(root);
}
private void inOrder(Node node){
if(node == null){
return;
}
inOrder(node.left);
System.out.println(node.t);
inOrder(node.right);
}
后序遍历
先递归访问左右子树,再访问自身节点。
public void postOrder(){
postOrder(root);
}
private void postOrder(Node node){
if(node == null){
return;
}
postOrder(node.left);
System.out.println(node.t);
postOrder(node.right);
}
6.3.2、前序遍历的非递归实现
基于栈的实现:
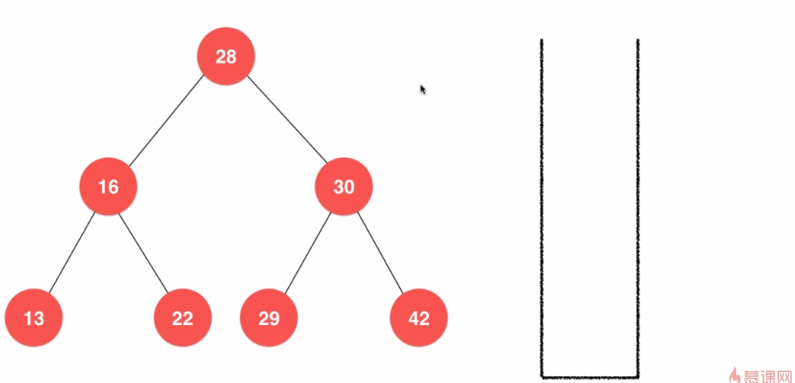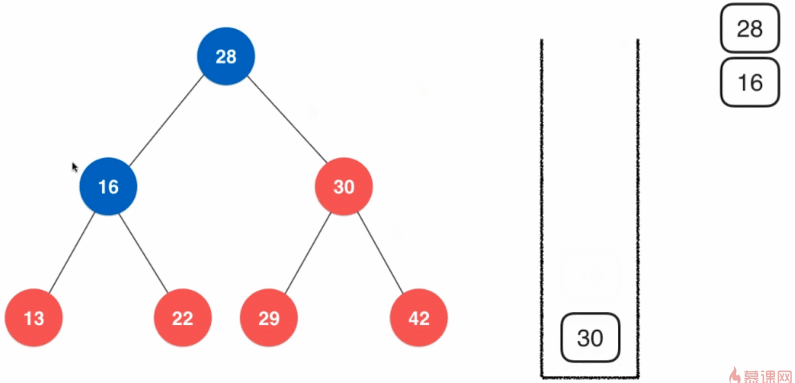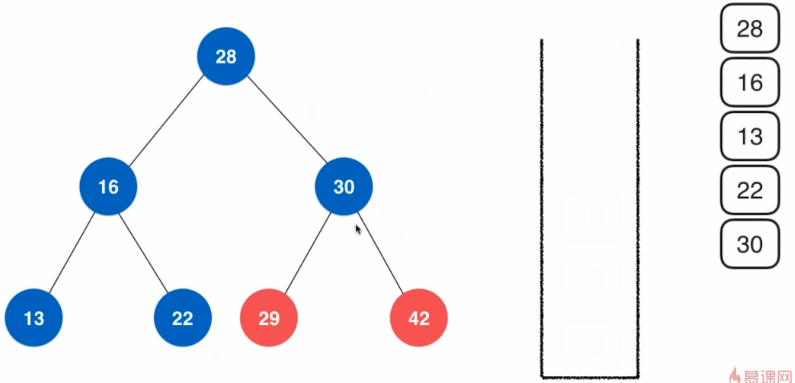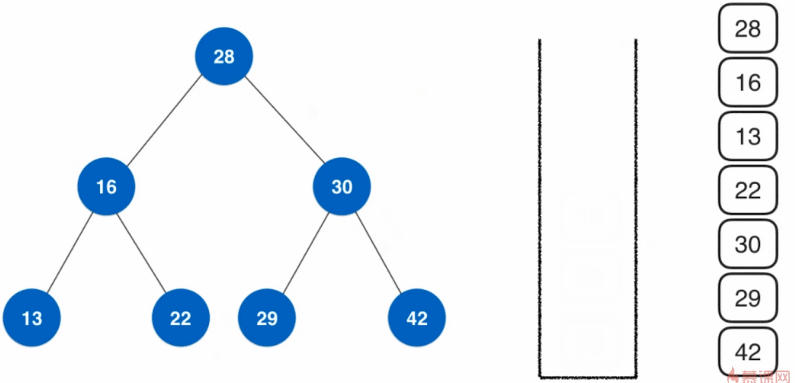
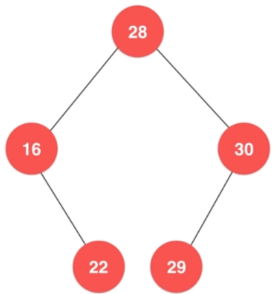
- 首先压入根结点28,再弹出根结点28
- 压入弹出的结点的右孩子30、左孩子16(先入后出原则);之后弹出左孩子16,压入左孩子16的右孩子22和左孩子13;再弹出右孩子30,压入右孩子30的右孩子42和左孩子29
- 重复步骤二,知道栈为空为止
//基于栈的前序遍历
public void preOrderNR(){
Stack<Node> nodeStack = new ArrayStack<>();
nodeStack.push(root);
while (!nodeStack.isEmpty()){
Node pop = nodeStack.pop();
System.out.println(pop.t);
if(pop.right != null){
nodeStack.push(pop.right);
}
if(pop.left != null){
nodeStack.push(pop.left);
}
}
}
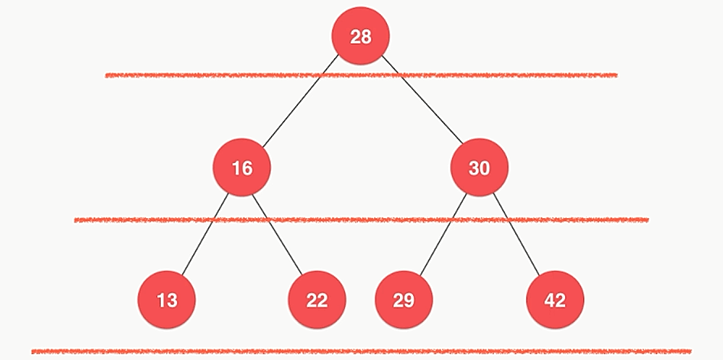
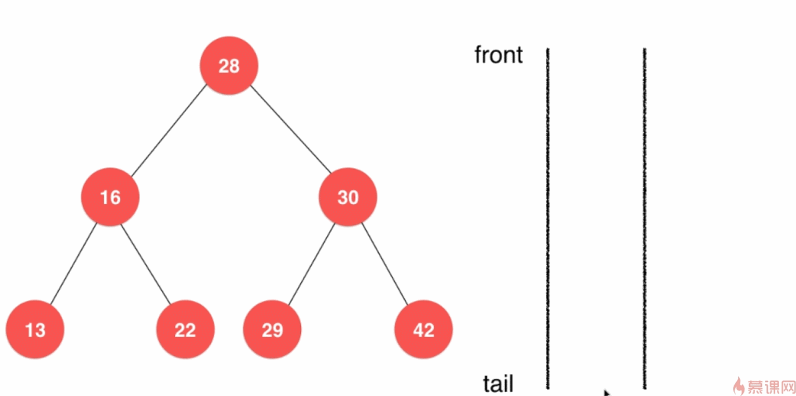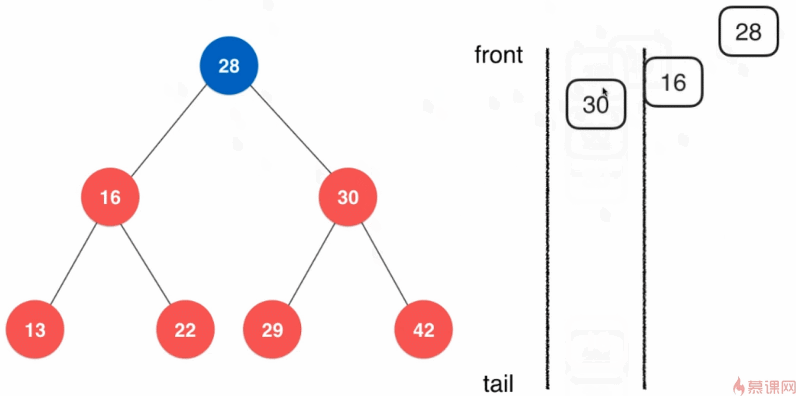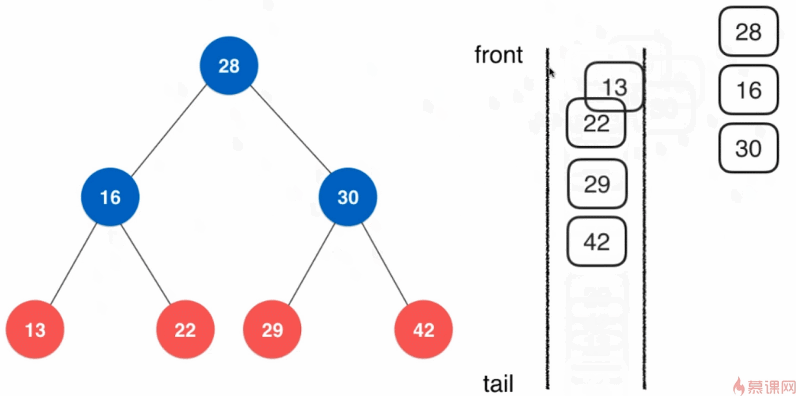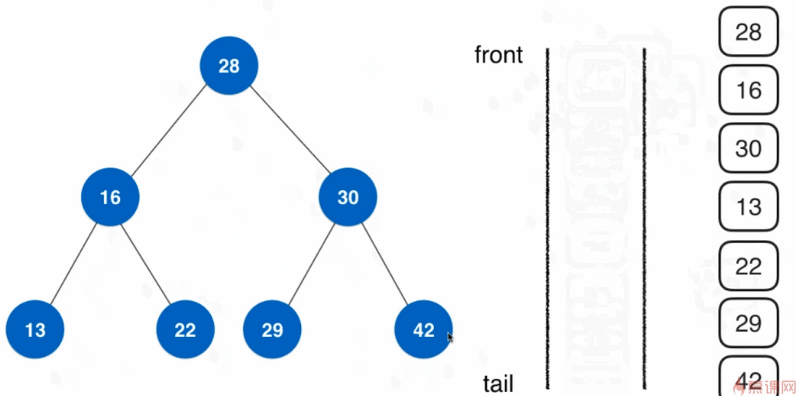
6.3.3、广度优先遍历(层序遍历)
之前实现的的遍历方式都是深度优先优先遍历。广度优先遍历的实现基于队列。
广度优先遍历的意义:
- 更快地找到问题的解
- 常用于算法设计中——最短路径
// 层序遍历
public void levelOrder(){
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()){
Node remove = queue.remove();
System.out.println(remove.t);
if(remove.left != null){
queue.add(remove.left);
}
if(remove.right != null){
queue.add(remove.right);
}
}
}
6.4、删除结点
6.4.1、删除最小/最大结点
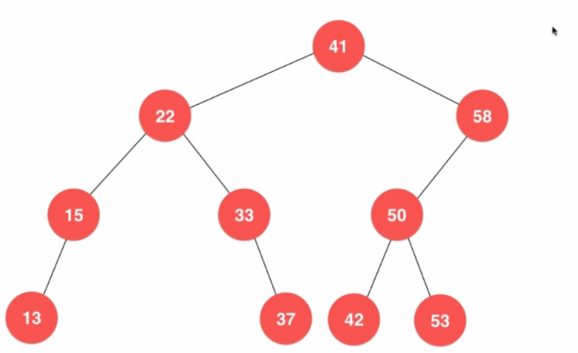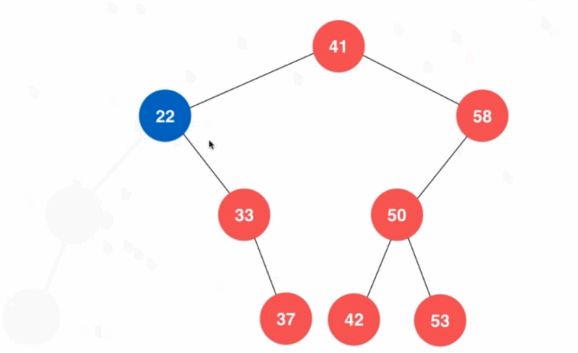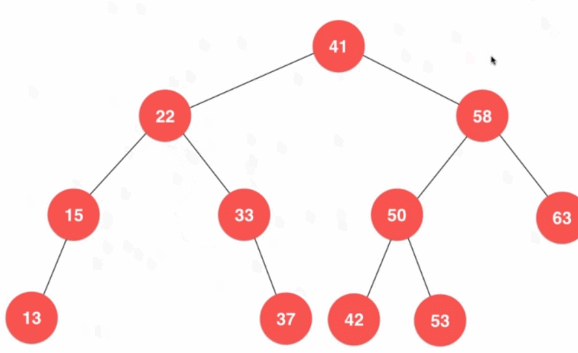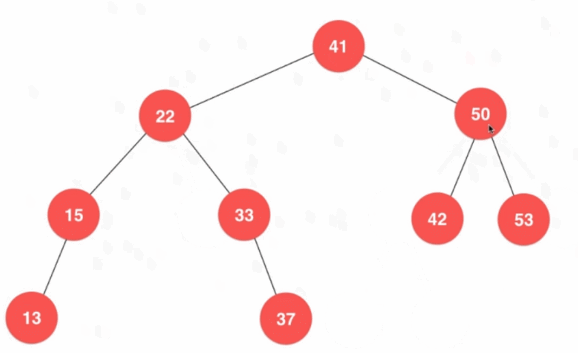
- 最小值位于树的最左侧,最大值位于树的最右侧
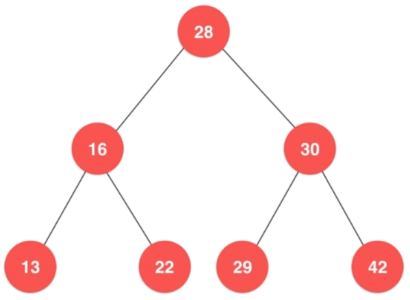
- 最值结点不一定是叶子结点
- 如果最小/最大结点是叶子结点,直接删除即可;否则还需要更新移除位置的结点
// 找到二分搜素树的最小元素
public T minimum(){
if(size == 0){
throw new IllegalArgumentException("树为空,删除最小值失败");
}
return minimum(root).t;
}
// 返回以node为根的二分搜索树的最小值所在的结点
private Node minimum(Node node){
if(node.left == null){
return node;
}
return minimum(node.left);
}
// 返回删除最小结点后的二分搜索树的根结点
// 删除掉以node为根的二分搜索树的最小结点
private Node removeMin(Node node) {
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// 查询二分搜素树的最大元素
public T maxmum(){
if(size == 0){
throw new IllegalArgumentException("树为空,删除最大值失败");
}
return maxmum(root).t;
}
// 返回以node为根的二分搜索树的最大值所在的结点
private Node maxmum(Node node){
if(node.right == null){
return node;
}
return maxmum(node.right);
}
public T removeMax(){
T ret = maxmum();
root = removeMax(root);
return ret;
}
// 返回删除最大结点后的二分搜索树的根结点
// 删除掉以node为根的二分搜索树的最大结点
private Node removeMax(Node node) {
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
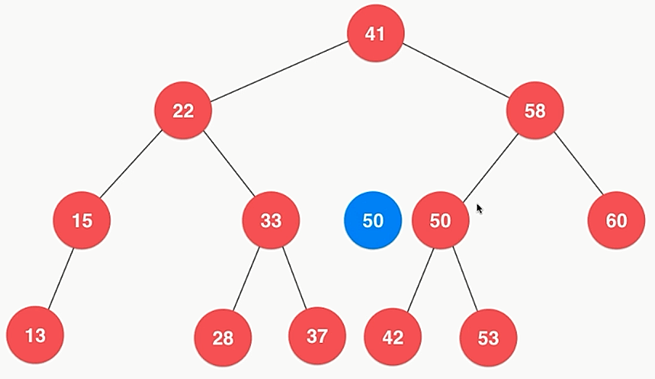
6.4.2、删除指定结点
- 删除只有左孩子的结点
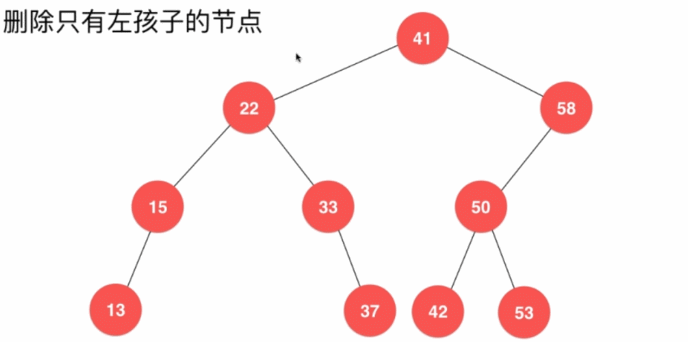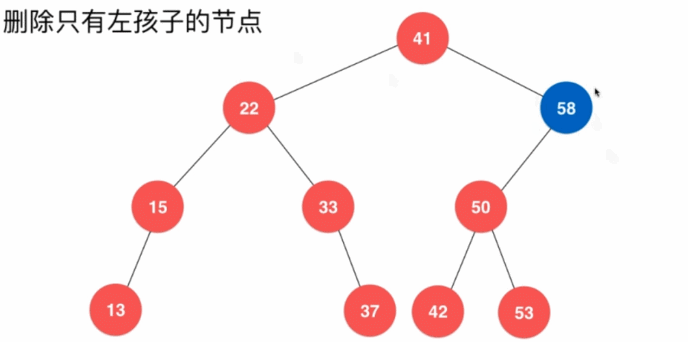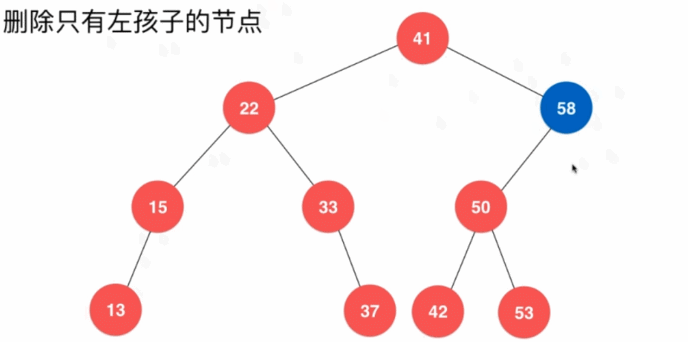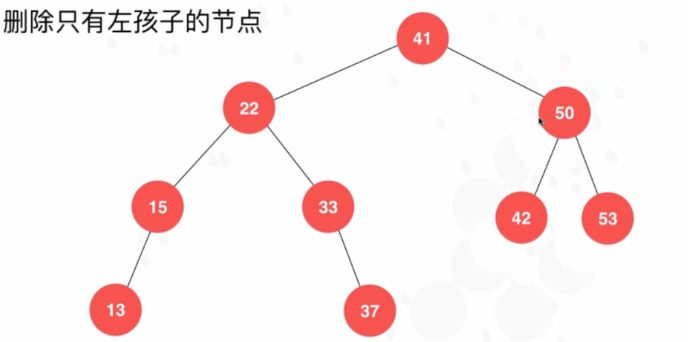
- 删除只有右子树的结点
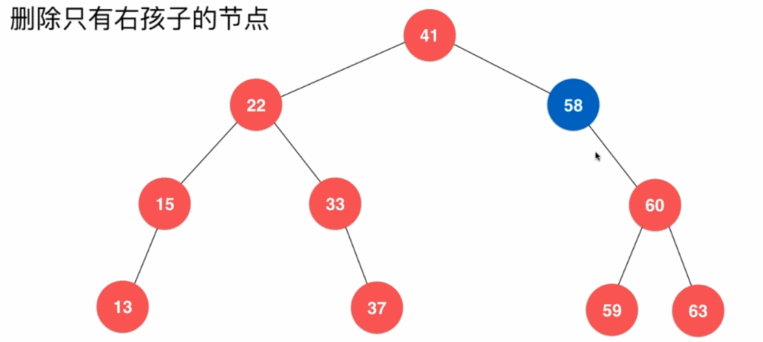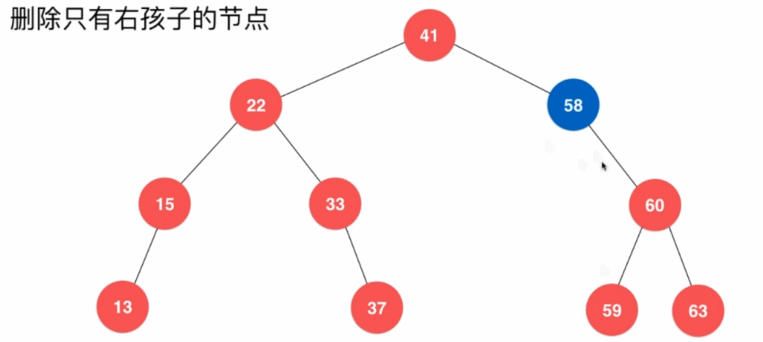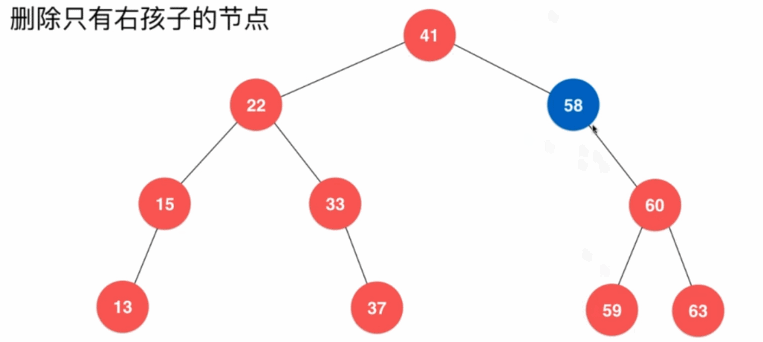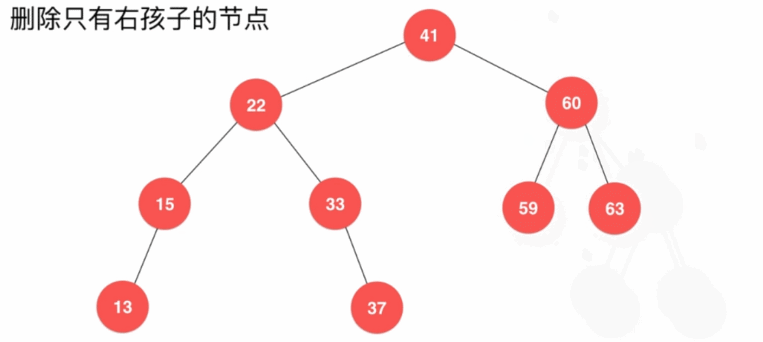
- 删除左右都有字树的结点,需要找到该结点子树中比该结点大的最小结点,使其作为新的当前结点
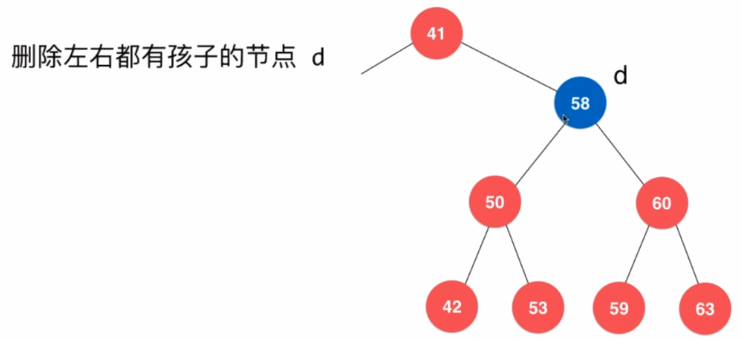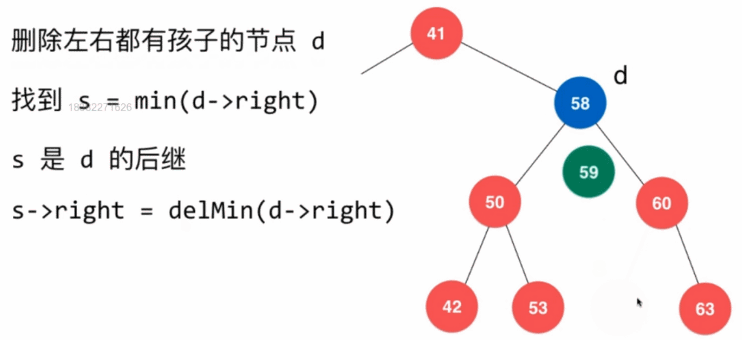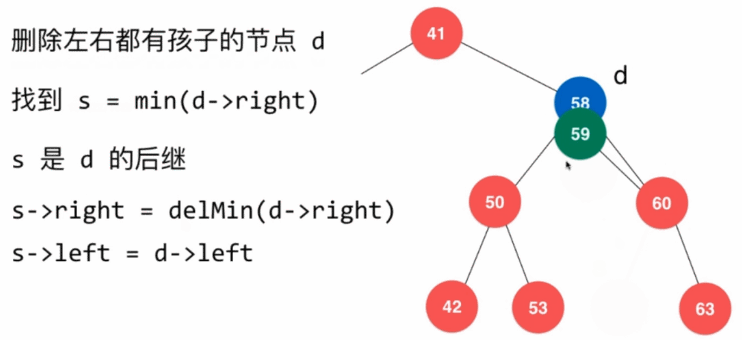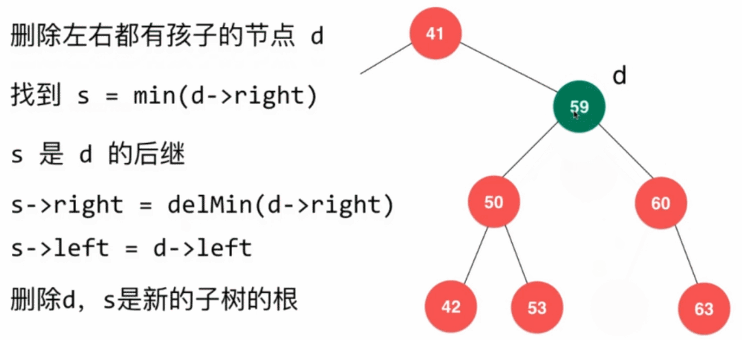
// 从二分搜索树中删除元素为e的节点
public void remove(E e){
root = remove(root, e);
}
// 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
// 返回删除节点后新的二分搜索树的根
private Node remove(Node node, E e){
if( node == null )
return null;
if( e.compareTo(node.e) < 0 ){
node.left = remove(node.left , e);
return node;
}
else if(e.compareTo(node.e) > 0 ){
node.right = remove(node.right, e);
return node;
}
else{ // e.compareTo(node.e) == 0
// 待删除节点左子树为空的情况
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size --;
return rightNode;
}
// 待删除节点右子树为空的情况
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size --;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
6.5、其他操作
- floor,二分搜索树中比当前结点小的最大结点
- ceil,二分搜索树中比当前结点大的最小结点
- rank,当前结点在二分搜索树中的排名
- select,rank的反向操作
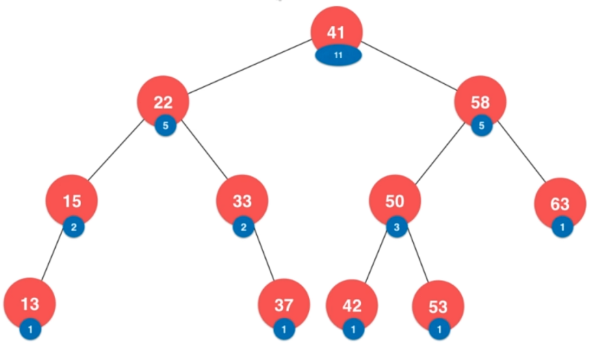
- 维护size的二分搜索树,每个结点都保存以当前结点为根的二分搜索树的结点总数
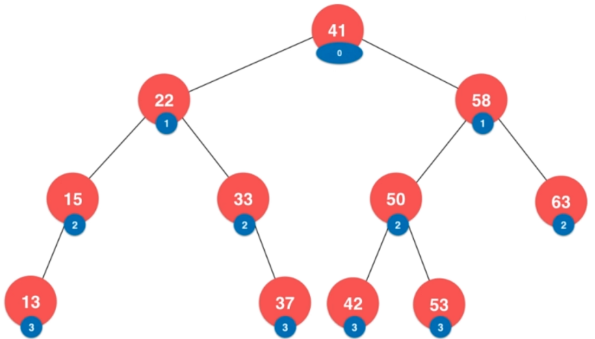
- 维护depth的二分搜索树,每个结点都保存当前结点在二分搜索树中的深度值
7、全部代码
package binarySearchTree;
import java.util.LinkedList;
import java.util.Stack;
import java.util.Queue;
//二分搜索树的泛型必须具有可比较性
public class BST<T extends Comparable<T>> {
private class Node{
public T t;
public Node left, right;
public Node(T t) {
this.t = t;
this.left = null;
this.right = null;
}
}
private Node root;
private int size;
public BST() {
root = null;
size = 0;
}
public int getSize() {
return size;
}
public boolean isEmpty(){
return size == 0;
}
// 从二分搜索树中添加新的元素e
public void add(T t){
root = add(root, t);
}
private Node add(Node node, T t){
if(node == null){
size++;
return new Node(t);
}
if(t.compareTo(node.t) < 0){
node.left = add(node.left, t);
}
else if(t.compareTo(node.t) > 0){
node.right = add(node.right, t);
}
return node;
}
public boolean contains(T t){
return contains(root, t);
}
private boolean contains(Node node, T t){
if(node == null){
return false;
}
if(t.compareTo(node.t) == 0){
return true;
}
else if(t.compareTo(node.t) > 0){
return contains(node.right, t);
}
else {
return contains(node.left, t);
}
}
//前序遍历
public void preOrder(){
preOrder(root);
}
private void preOrder(Node node){
if(node == null){
return;
}
System.out.println(node.t);
preOrder(node.left);
preOrder(node.right);
}
//基于栈的前序遍历的非递归实现
public void preOrderNR(){
Stack<Node> nodeStack = new Stack<>();
nodeStack.push(root);
while (!nodeStack.isEmpty()){
Node pop = nodeStack.pop();
System.out.println(pop.t);
if(pop.right != null){
nodeStack.push(pop.right);
}
if(pop.left != null){
nodeStack.push(pop.left);
}
}
}
// 中序遍历
public void inOrder(){
inOrder(root);
}
private void inOrder(Node node){
if(node == null){
return;
}
inOrder(node.left);
System.out.println(node.t);
inOrder(node.right);
}
// 后序遍历
public void postOrder(){
postOrder(root);
}
private void postOrder(Node node){
if(node == null){
return;
}
postOrder(node.left);
System.out.println(node.t);
postOrder(node.right);
}
// 层序遍历
public void levelOrder(){
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()){
Node remove = queue.remove();
System.out.println(remove.t);
if(remove.left != null){
queue.add(remove.left);
}
if(remove.right != null){
queue.add(remove.right);
}
}
}
// 查询而二分搜素树的最小元素
public T minimum(){
if(size == 0){
throw new IllegalArgumentException("树为空,删除最小值失败");
}
return minimum(root).t;
}
// 返回以node为根的二分搜索树的最小值所在的结点
private Node minimum(Node node){
if(node.left == null){
return node;
}
return minimum(node.left);
}
// 查询而二分搜素树的最大元素
public T maxmum(){
if(size == 0){
throw new IllegalArgumentException("树为空,删除最大值失败");
}
return maxmum(root).t;
}
// 返回以node为根的二分搜索树的最大值所在的结点
private Node maxmum(Node node){
if(node.right == null){
return node;
}
return maxmum(node.right);
}
public T removeMin(){
T ret = minimum();
root = removeMin(root);
return ret;
}
// 返回删除最小结点后的二分搜索树的根结点
// 删除掉以node为根的二分搜索树的最小结点
private Node removeMin(Node node) {
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
public T removeMax(){
T ret = maxmum();
root = removeMax(root);
return ret;
}
// 返回删除最大结点后的二分搜索树的根结点
// 删除掉以node为根的二分搜索树的最大结点
private Node removeMax(Node node) {
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
public void remove(T t){
root = remove(root, t);
}
private Node remove(Node node, T t) {
if(node == null){
return null;
}
if(t.compareTo(node.t) > 0){
node.right = remove(node.right, t);
return node;
}
else if(t.compareTo(node.t) < 0){
node.left = remove(node.left, t);
return node;
}
else {
// 当前待删除结点只有右孩子的情况
if(node.left == null){
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
// 当前待删除结点只有左孩子的情况
if(node.right == null){
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
// 当前待删除结点左右孩子均不为空的情况
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
@Override
public String toString() {
StringBuilder builder = new StringBuilder();
generateBSTString(root, 0, builder);
return builder.toString();
}
// 生成二分搜索树的字符串
private void generateBSTString(Node node, int depth, StringBuilder builder){
if(node == null){
builder.append(generateDepthString(depth) + "null
");
return;
}
builder.append(generateDepthString(depth) + node.t + "
");
generateBSTString(node.left, depth+1, builder);
generateBSTString(node.right, depth+1, builder);
}
// 生成深度信息的字符串
private String generateDepthString(int depth) {
StringBuilder builder = new StringBuilder();
for (int i=0; i<depth; i++){
builder.append("--");
}
return builder.toString();
}
}