Large scale machine learning 大规模机器学习
Learning with large datasets
- 从事大规模机器学习的前提是拥有大量的数据。
- 使用合理的方法处理大数据集,如高方差时增加训练集会提高性能,而高偏差时增加训练集却不会有用。
Stochastic gradient descent
之前了解的梯度下降是指批量梯度下降;如果我们一定需要一个大规模的训练集,我们可以尝试使用随机梯度下降法(SGD)来代替批量梯度下降法。
在随机梯度下降法中,我们定义代价函数为一个单一训练实例的代价:
算法步骤:
-
Randomly shuffle (reorder) training examples 将数据打乱
-
Repeat{
//外层一般循环1~10次 for (i := 1,dots,m) {
( heta_j := heta_j - alpha(h_ heta(x^{(i)}) - y^{(i)})x_j^{(i)}) (for (j = 0,dots,n))
}
}
随机梯度下降算法实际上就是扫描所有的训练样本。先对第1组训练样本进行梯度下降,包括调参过程;然后转向第2个训练样本,对第2个训练样本计算一小步的梯度下降,这个过程也包括调参,接着转向第3个训练样本……
这种重复循环会遍历整个训练集,一开始打乱训练集保证了在扫描训练集时对训练集样本的随机访问,此操作加快了随机梯度下降的收敛。
对比:
批量梯度下降的收敛过程倾向于一条近似的直线,一直找到全局最小值;随机梯度下降不需要对所有(m)个训练样本求和来得到梯度项,而是只需要对单个训练样本求出梯度项,每次只需关注一个训练样本,每次迭代更快。
批量梯度下降和随机梯度下降算法的收敛过程是不同的,实际上,随机梯度下降是在某个靠近全局最小值的区域内徘徊,而不是真的逼近全局最小值并停留在那个点,不过其最终也会得到一个很接近全局最小值的参数。这对于绝大多数的实际应用的目的来说,已经足够了。
随机梯度下降算法收敛比较快。
Mini-batch gradient descent
Batch gradient descent: Use all (m) examples in each iteration 批量梯度下降算法:每次迭代都用到所有(m)个样本
Stochastic gradient descent: Use 1 example in each iteration 随机梯度下降算法:每次迭代只需使用1个样本
Mini-batch gradient descent: Use b examples in each iteration 小批量梯度下降法:每次迭代使用(b)个样本,其中(b)是一个称为“小批量尺寸”的参数,通常选择(b = 10),变化范围在(2) ~ (100)之间。
算法描述:
Say (b = 10), (m = 1000). //假设(b = 10), (m = 1000).
Repeat {
for (i = 1,11,21,31,dots,991) {
( heta_j := heta_j - alphafrac{1}{10}sum_{k=i}^{i+9}(h_ heta(x^{(k)}) - y^{(k)})x_j^{(k)}) (for every (j = 0,dots,n))
}
}
总结:
使用小批量梯度下降算法,在处理了前10个样本之后,就可以开始优化参数( heta),因此不需要扫描整个训练集,因此小批量梯度下降算法比批量梯度下降算法快。
小批量梯度下降算法在有好的向量化实现时,比随机梯度下降算法好,在这种情况下,10个样本求和可以使用一种更向量化的方法实现,允许部分并行计算10个样本的和。
但是一个合适的(b)的值的确定通常会浪费很多时间。
Stochastic gradient descent convergence
如何确保调试过程已完成并且收敛到合适的位置?如何调整随机梯度下降算法中学习速率(alpha)的值?
Checking for convergence
批量梯度下降算法 vs. 随机梯度下降算法
-
Batch gradient descent: Plot (J_{train( heta)}) as a function of the number of iterations of gradient descent. (J_{train}( heta) = frac{1}{2m}sum_{i=1}^m(h_ heta(x^{(i)}) - y^{(i)})^2). 批量梯度下降算法中确定收敛的方法是,画出最优化的代价函数关于迭代次数的变化。需保证代价函数在每次迭代中都是下降的。
代价函数的求和计算需要考虑整个的训练集,故此方法在训练集很小时很容易完成,在训练集很大时较难完成。
-
随机梯度下降算法每次只考虑一个样本,不需要扫描全部的训练集。故可以通过下述方法进行检测:
Stochastic gradient descent: (cost( heta,(x^{(i)},y^{(i)})) = frac{1}{2}(h_ heta(x^{(i)}) - y^{(i)})^2). During learning, compute (cost( heta,(x^{(i)},y^{(i)}))) before updating ( heta) using ((x^{(i)},y^{(i)})). 沿用之前定义的(cost)函数。在随机梯度下降法对训练集进行扫描时,使用某个样本((x^{(i)},y^{(i)}))来更新( heta)前计算(cost)函数。
Every 1000 iterations (say), plot (cost( heta,(x^{(i)},y^{(i)}))) averaged over the last (1000) examples processed by algorithm. 最后,为了检查随机梯度下降算法的收敛性,可以每(1000)次迭代画出前一步中计算出的(cost)函数。将(cost)函数画出来,并对算法处理的最后(1000)个样本的(cost)值求平均值,这样会有效地估计出算法在最后(1000)个样本上的表现。
随机梯度下降算法收敛性
以每次迭代的最后(1000)个样本的平均值为点作图为例,对于图形对应的分析如下: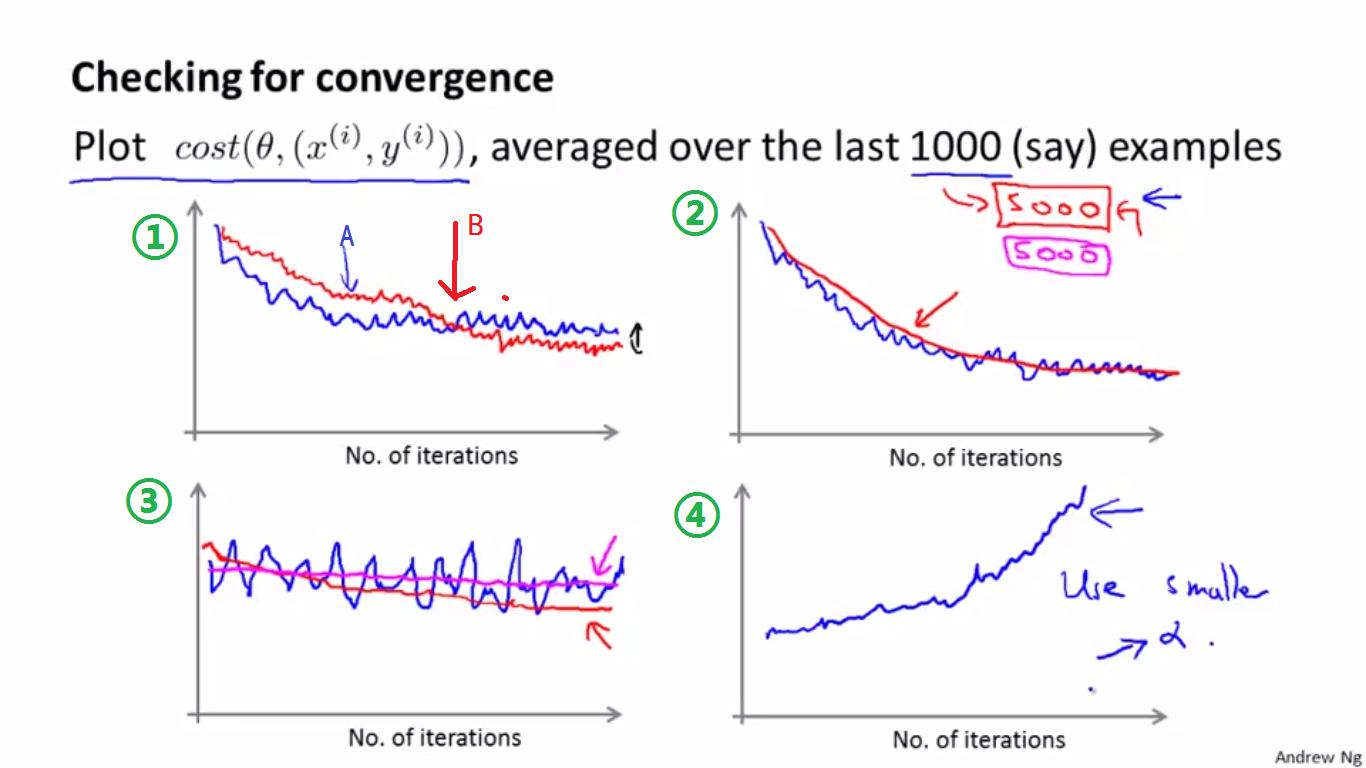
- 图①中:蓝色的曲线在A点趋于平缓,说明算法已经趋于收敛,因随机梯度下降算法不直接收敛于最小值,因此最后会来回震荡。若减小学习速率(alpha)的值,则可能会出现红色的曲线,其收敛于B点,因(alpha)变小,所以收敛速度变慢,且因为(alpha)较小,最后震荡的幅度也比较小。
- 图②中:(1000)个训练样本得到了蓝色的曲线,若将样本数从(1000)增加到(5000),则会出现红色的更加平滑的曲线。
- 图③中:蓝色的直线一直很平坦,说明算法并没有很好地学习。若增大样本数量到(5000),可能会出现红色曲线。若增大样本数量,仍然得到紫色曲线(即仍然是平坦的),则说明算法确实没有学习好,需要调整(alpha)或者改变特征等。
- 图④中:若出现不降反增的情况,说明算法正在发散,需要减小(alpha)的值。
总结:
- 曲线是来回震荡,是因为有噪音。
- 若曲线看起来噪音很大,或是老是上下波动,则尝试增大平均的样本数量。
- 若发现代价值在上升,则换一个小点的(alpha)值。
Stochastic gradient descent
随机梯度下降算法最后不会收敛于某一个最优值,而是会在最优值边缘来回震荡,在大多数的随机梯度下降算法中,学习速率(alpha)一般是保持不变的。若想要随机梯度算法收敛于全局最优值,可以随时间的变化减小学习速率(alpha)的值,所以,一种典型的方法将(alpha)的值设置为:
在这个公式中,随着迭代次数的增加,(alpha)的值会越来越小,因此震荡都会越来越小,直到最终收敛到几乎靠近全局最小值的地方。
一般情况下,我们会令(alpha)为一个常数,而不是给出(const1)和(const2)。因确定这两个常数比较繁琐,且在平时的实践应用中令(alpha)为常数的结果能够接近全局最小值,所以很少采用逐渐减小(alpha)值的方法。
Online learning
在线学习机制让我们可以模型化问题。在连续的数据流涌进来,需要一个算法来从中学习的时候来模型化问题。
Example1
假设有一个在线包裹系统,用户将包裹从A地运往B地,网站会给出一个价格,用户可能会接受此价格((y=1))或者不接受((y=0))。
特征(x)用于存储用户的属性、出发地、目的地和网站给出的价格,我们希望去学习(P(y=1|x; heta))去优化价格,我们可以使用逻辑回归或者神经网络来学习,先来考虑逻辑回归。
Repeat forever {
Get ((x, y)) corresponding to user
Update ( heta) using ((x, y)): ( heta_j := heta_j - alpha(h_ heta(x) - y)x_j) ((j = 0,dots,n))
}
算法之所以没有使用((x^{(i)},y^{(i)})),是因为在线学习机制将某一样本完之后,就丢弃这个样本。因此若你有很多连续的数据流,在线学习机制将会非常有效,而若你只有少量数据,则选择其他的算法而不选择在线学习。
在线学习算法可以对正在变化的用户偏好进行调适,特别地,随着时间的变化,大的经济环境发生变化,用户们可能会对价格变得非常敏感,然后愿意支付更高的价格,又或者,有一批新的类型的用户涌入网站,在线学习算法可以根据变化着的用户偏好进行调适,而且从某种程度上可以跟进变化着的用户群体所愿意支付的价格。
在线学习系统能够产生这种作用的原因是随着时间的变化,参数( heta)不断变化和更新,会逐渐调适到最新的用户群体所应该体现出来的参数。
Example2
产品搜索:通过用户搜索的关键词推荐用户最有可能点击的10部手机。
(x)用于存储手机的的特征、用户搜索匹配这部手机名称的次数、用户搜索匹配这部手机描述的次数等。
若用户点击这部手机,则(y = 1),否则(y = 0)。
学习(p(y = 1|x; heta))。
Other examples
- Choosing special offers to show user. 选择优惠信息展示给用户
- Customized selection of news articles. 订制新闻选择
- Product recommendation. 产品推荐
总结
在线学习机制与随机梯度下降算法非常相似,只是在线学习不是使用一个固定的数据集,而是从一个样本中学习之后丢弃这个样本,如果你有一个连续的数据流,那么这个算法是非常值得考虑的。
在线学习的优点:若你有一个变化的用户群,又或者你正在预测变化的事情,在线学习可以慢慢调适到好的假设以便适应用户的最新行为。
Map-reduce and data parallelism
Map-reduce 映射约减
如果我们用批量梯度下降算法来求解大规模数据集的最优解,我们需要对整个训练集进行循环,计算偏导数和代价,再求和,计算代价非常大。如果我们能够将我们的数据集分配给不多台计算机,让每一台计算机处理数据集的一个子集,然后我们将计所的结果汇总在求和。这样的方法叫做映射约减。
以(m = 400)的批量梯度下降算法为例(实际上(m)会非常大)。
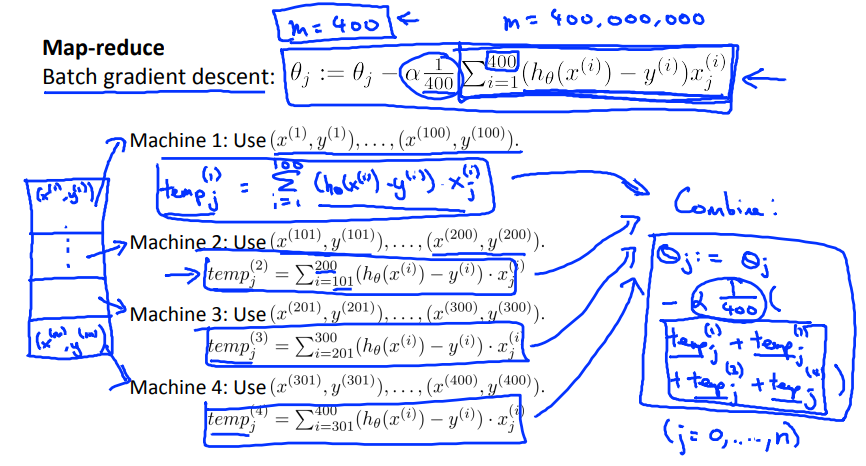
通过将数据分散到4台机器上,这样运行效率理论上会增加4倍。
| Machine no. | Sample | Computation |
|---|---|---|
| 1 | 1-100 | (temp^{(1)} = sum_{i=1}^{100}(h_ heta(x^{(i)})-y^{(i)})x_j^i) |
| 2 | 101-200 | (temp^{(2)} = sum_{i=101}^{200}(h_ heta(x^{(i)})-y^{(i)})x_j^i) |
| 3 | 201-300 | (temp^{(3)} = sum_{i=201}^{300}(h_ heta(x^{(i)})-y^{(i)})x_j^i) |
| 4 | 301-400 | (temp^{(4)} = sum_{i=301}^{400}(h_ heta(x^{(i)})-y^{(i)})x_j^i) |
--> Result: ( heta_j := heta_j - alphafrac{1}{400}(temp^{(1)}+temp^{(2)}+temp^{(3)}+temp^{(4)})).
总结:对于一些训练样本,我们希望通过使用4台计算机并行的运行机器学习算法,那么我们将训练样本尽量均匀的四等分,然后将训练样本的自己送给4台不同的计算机,每台计算机都对一份训练数据进行求和运算,最后这4个求和结果被送到一台中心计算服务器,由它来对结果进行汇总。因为每台计算机都可以完成四分之一的计算工作,因此会得到4倍的加速,但是实际上因为网络延迟等一些其他的原因,效率增加不到4倍。但是这种算法确实让我们能够处理通常单台计算机无法处理的大规模数据。
Map-reduce and summation over the training set
只要算法的主要计算部分可以表示为训练样本的求和,那么就可以考虑使用映射约减技术。
Multi-core machines
上面的情况是利用若干台机器,将数据的计算分散到各台机器上,实际上,我们也可以在一台计算机上实现Map Reduce,即利用现代计算机的多核系统。通过将训练样本分成几份,每一个核处理其中一部分,也能实现并行的效果,而且因为数据始终还是在一台机器上运行的,因此不存在网络延迟的影响。
很多高级的线性代数函数库已经能够利用多核CPU的多个核心来并行地处理矩阵运算,这也是算法的向量化实现如此重要的缘故(比调用循环快)。