洛谷——P3906 Geodetic集合

P3906 Geodetic集合

题目描述

图G是一个无向连通图，没有自环，并且两点之间至多只有一条边。我们定义顶点v，u最短路径就是从v到u经过边最少的路径。所有包含在v-u的最短路径上的顶点被称为v-u的Geodetic顶点，这些顶点的集合记作I(v, u)。

我们称集合I(v, u)为一个Geodetic集合。

例如下图中，I(2, 5)={2, 3, 4, 5}，I(1, 5)={1, 3, 5}，I(2, 4)={2, 4}。

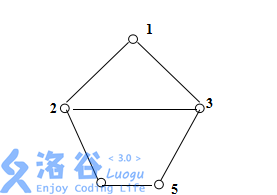
给定一个图G和若干点对v,u，请你分别求出I(v, u)。

输入输出格式

输入格式：

输入文件geo.in，第一行为两个整数n,m，分别表示图G的顶点数和边数（顶点编号1-n，n≤40）。下接m行，每行两个整数a,b表示顶点a和b之间有一条无向边。

第m+2行有一个整数k，表示给定的点对数。下接k行，每行两个整数v,u。。

输出格式：

输出文件geo.out，共k行，每行对应输入文件中每一个点对v,u，按顶点编号升序输出I(v, u)。同一行的每个数之间用空格分隔。

输入输出样例

输入样例#1： 复制

5 6
1 2
1 3
2 3
2 4
3 5
4 5
3
2 5
5 1
2 4

输出样例#1： 复制

2 3 4 5
1 3 5
2 4

解题报告：

题目大意:给你一个无向连通图，询问两点之间最短路径上的点

spfa 跑最短路，记录到达每个节点最短路径上的的前驱即可，不过前驱可能有好几个，vector<int>G[N]存储即可

此题有个坑点，一定要去重！！！

#include<bits/stdc++.h>

#define N 101001
using namespace std;

int n,m,head[N],tot;
bool pvis[N];
struct nod {
    int to,next;
} e[N];
void add(int u,int v) {
    e[++tot].to=v,e[tot].next=head[u],head[u]=tot;
}

int q,d[N];
bool vis[N];
queue<int>Q;
vector<int>G[50];
void spfa(int x) {
    while(!Q.empty()) Q.pop();
    Q.push(x);
    for(int i=1; i<=n; i++) G[i].clear();
    memset(vis,0,sizeof(vis));
    memset(d,0x3f,sizeof(d));
    vis[x]=1,d[x]=0;
    while(!Q.empty()) {
        int u=Q.front();
        Q.pop();
        vis[u]=0;
        for(int i=head[u]; i; i=e[i].next) {
            int v=e[i].to;
            if(d[v]>d[u]+1) {
                d[v]=d[u]+1;
                if(!vis[v]) {
                    G[v].clear();
                    G[v].push_back(u);
                    Q.push(v);
                    vis[v]=1;
                }
            } else if(d[v]==d[u]+1) {
                G[v].push_back(u);
            }
        }
    }
}
int an[N],tpt;
void dg(int u,int a) {
    int sz=G[u].size();
    an[++tpt]=u;
    for(int i=0; i<sz; i++) {
        int v=G[u][i];
        if(v==a) continue;
        dg(v,a);
    }
}

int main() {
    scanf("%d%d",&n,&m);
    for(int a,b,i=1; i<=m; i++) {
        scanf("%d%d",&a,&b);
        add(a,b),add(b,a);
    }
    scanf("%d",&q);
    for(int a,b,i=1; i<=q; i++) {
        scanf("%d%d",&a,&b);
//        memset(pvis,0,sizeof(pvis));
        spfa(a);
        memset(an,0,sizeof(an));
        tpt=0;
        dg(b,a);
        an[++tpt]=a;
        sort(an+1,an+1+tpt);
        for(int j=1; j<=tpt; j++){
            if(an[j]!=an[j+1]) printf("%d ",an[j]);
        }
        puts("");
    }
    return 0;
}