题意:
两个人一个从左上角一个从左下角分别开始走分别走向右下角和右上角,(矩阵每个格子有数)问到达终点后可以得到的最大数是多少,并且条件是他们两个相遇的时候那个点的数不能算
思路:
首先这道题如果暴力搜索一般是gg了,所以考虑动态规划
我们设起点为st(1,1),终点为ed(n,m),相遇的点为now(i,j)
问题转化为计算st→now + now→ed的值(不包含now)
这个问题可以分解为求st→now和now→ed的值,st→now = dp[st][now],那么now→ed怎么求呢
可以反过来思考,now→ed其实就是ed→now的值,反向dp即可
还有个很重要的问题
在相遇的时候,即在点now时,每条路径只能走相对的边,如图
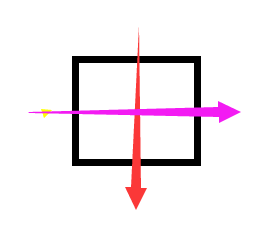
如果走的是临边,效果可能不一样,可以试试。。。
代码:
#include<iostream>
#include<cstring>
#define max(a, b) ((a)>(b)?(a):(b))
using namespace std;
typedef long long ll;
const int maxn = 1010;
int mp[maxn][maxn];
int dp1[maxn][maxn],dp2[maxn][maxn],dp3[maxn][maxn],dp4[maxn][maxn];
int main() {
memset(dp1, 0, sizeof dp1);
memset(dp2, 0, sizeof dp2);
memset(dp3, 0, sizeof dp3);
memset(dp4, 0, sizeof dp4);
int n,m;
scanf("%d %d", &n,&m);
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
scanf("%d", &mp[i][j]);
}
}
//从右下 走
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
dp1[i][j] = max(dp1[i-1][j], dp1[i][j-1]) + mp[i][j];//到点(i,j)有两种方法,以下如此
}
}
//从左上 走
for(int i = n; i >= 1; i--) {
for(int j = m; j >= 1; j--) {
dp2[i][j] = max(dp2[i+1][j], dp2[i][j+1]) + mp[i][j];
}
}
//从右上 走
for(int i = n; i >= 1; i--) {
for(int j = 1; j <= m; j++) {
dp3[i][j] = max(dp3[i+1][j], dp3[i][j-1]) + mp[i][j];
}
}
//从左下 走
for(int i = 1; i <= n; i++) {
for(int j = m; j >= 1; j--) {
dp4[i][j] = max(dp4[i-1][j], dp4[i][j+1]) + mp[i][j];
}
}
ll ans = -1;
for(int i = 2; i < n; i++) {
for(int j = 2; j < m; j++) {
ans = max(dp1[i-1][j] + dp2[i+1][j] + dp3[i][j-1] + dp4[i][j+1], ans);
ans = max(dp1[i][j-1] + dp2[i][j+1] + dp3[i+1][j] + dp4[i-1][j], ans);
//把横向穿过和纵向穿过,两者进行枚举
}
}
printf("%d
", ans);
return 0;
}