二叉搜索树（Binary Search Tree）--C语言描述(转)

图解二叉搜索树概念

二叉树呢，其实就是链表的一个二维形式，而二叉搜索树，就是一种特殊的二叉树，这种二叉树有个特点：对任意节点而言，左孩子（当然了，存在的话）的值总是小于本身，而右孩子（存在的话）的值总是大于本身。

下面来介绍在此种二叉树结构上的查找，插入，删除算法思路。

查找：因为这种结构就是为了来方便查找的，所以查找其中的某个值很容易，从根开始，小的往左找，大的往右找，不大不小的就是这个节点了；

代码很简单，这里就不写了。

插入：插入一样的道理，从根开始，小的往左，大的往右，直到叶子，就插入。

代码：

int Insert(BSTree *T,data_type data)//插入数据
{
    BSTree newnode,p;
    newnode = (BSTree)malloc(sizeof(BSNode));
    newnode->lchild = newnode->rchild = NULL;
    newnode->data = data;
    if(*T == NULL)
    {
        *T = newnode;
    }
    else
    {
        p = *T;
        while(1)
        {
            if(data == p->data)
            {
                return 0;//数值已存在，不能插入
            }
            else if(data > p->data)
            {
                if(p->rchild == NULL)//右孩子为空，插入
                {
                    p->rchild = newnode;
                    return 1;
                }
                else        //继续向下找
                {
                    p = p->rchild;
                }
            }
            else
            {
                if(p->lchild == NULL)//左孩子为空，插入
                {
                    p->lchild = newnode;
                    return 1;
                }
                else        //继续向下找
                {
                    p = p->lchild;
                }
            }
        }
    }
}

删除：而结点的删除则比较麻烦，是这个结构中最难的一环，因为我们删除的结点不一定是叶子结点，是叶子结点很好办，但是如果是二叉树中的一个结点，则涉及到删除后的连接问题。

删除一共分为以下四种情况：

1.删除结点为叶子结点：这个就不说了，删除很简单。

2.删除结点不是叶子结点，其左子树不为空，右子树为空：这种情况，只需将其父结点与其右孩子结点连接，然后删除，例如删除下图的40，就是连接30与35。

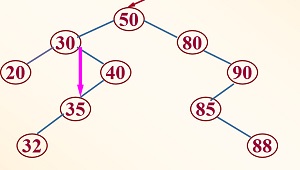
3.删除结点不是叶子结点，其右子树不为空，左子树为空：这种情况，只需将其父结点与其左孩子结点连接，然后删除，例如删除下图的80，就是连接50和90

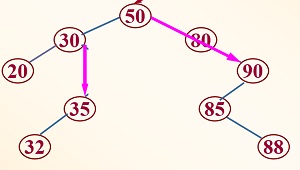
4.删除结点不是叶子结点，左右子树都不为空，这种情况最复杂，咋们单独分析分析。

此种情况下，总的删除思想就是：把这个结点往下挪，直到它变为叶子为止。挪移规则：即和此结点下的最大孩子的值交换，把删除该结点转换为删除孩子结点的操作。

当然会出现这种情况，交换后此结点仍然不是叶子结点，那就继续按照挪移规则直到将改结点挪移成叶子结点。举例如图：

首先是我自己写的一个删除算法，借用了查找函数。

我的想法还是以前链表的删除思路，删除一个结点需要记录前一个结点，所以我就是用fa记录删除结点的父结点，然后操作的。

所以借用的查找函数就不仅仅只是返回结点地址，也要返回父结点地址。

BSTree Find(BSTree T,data_type data,BSTree *target) //查找函数,并返回父亲结点地址
{
    if(T == NULL)//二叉树为空
    {
        *target = NULL;
        return NULL;
    }
    else if(T->data == data)//树根即为要查找的结点
    {
        *target = T;
        return NULL;
    }
    else
    {
        while(T)
        {
            if(T->lchild && T->lchild->data == data)
            {
                *target = T->lchild;
                return T;
            }
            if(T->rchild && T->rchild->data == data)
            {
                *target = T->rchild;
                return T;
            }
            if(data > T->data)
            {
                T = T->rchild;
            }
            if(data < T->data)
            {
                T = T->lchild;
            }
        }
        return NULL;
    }
}

int Delete1(BSTree *T,data_type data)//删除
{
    BSTree fa,target;
    if(*T == NULL)//树为空
    {
        return 0;
    }
    fa = Find(*T,data,&target);//fa为删除结点的父结点，target为删除结点
    if(target->lchild == NULL)    //删除结点左子树为空，右子树不为空的情况(左右子树都为空的情况也适用)
    {
        if(fa == NULL && target->rchild == NULL)//树只存在根结点的情况
        {
            free(*T);
            *T = NULL;
            return 1;
        }
        if(fa->rchild == target)
        {
            fa->rchild = target->rchild;
            free(target);
            return 1;
        }
        if(fa->lchild == target)
        {
            fa->lchild = target->rchild;
            free(target);
            return 1;
        }
    }
    else if(target->rchild == NULL)//删除结点右子树为空，左子树不为空的情况
    {
        if(fa->rchild == target)
        {
            fa->rchild = target->lchild;
            free(target);
            return 1;
        }
        if(fa->lchild == target)
        {
            fa->lchild = target->lchild;
            free(target);
            return 1;
        }
    }
    else    //左右子树都不为空的情况
    {
        if(target->lchild->rchild == NULL)    //孩子结点中最大值结点为target->lchild
        {
            target->data = target->lchild->data;
            return Delete1(&(target->lchild),target->data);
        }
        else        //孩子结点中最大值结点为target->lchild->rchild.....->rchild
        {
            BSTree p1,p2;
            p2 = target->lchild;
            p1 = p2->rchild;
            while(p1->rchild != NULL)//循环找到最大值结点
            {
                p2 = p1;
                p1 = p1->rchild;
            }
            target->data = p1->data;
            return Delete1(&(p2->rchild),p1->data);
        }
    }
}

然后写完之后感觉自己的算法篇幅好大，貌似有点麻烦，于是在网上找了一下相关的二叉搜索树的删除算法，发现一个很精妙小巧的算法，将递归用的非常漂亮。

当然，算法思路都是差不多的，所以效率上应该没有什么很大的差别，不过这个算法递归思想用的很赞，值得学习一下。

建议先把上面我写的算法看明白了，在看下面的这个。

//a：删除叶子结点，只要将其双亲结点链接到它的指针置空即可。
//b：删除单支结点，只要将其后继指针链接到它所在的链接位置即可
//c：删除双支结点，一般采用的方法是首先把它的中序前驱结点的值赋给该结点的值域，
//然后再删除它的中序前驱结点，若它的中序前驱结点还是双支结点，继续对其做同样的操作，
//若是叶子结点或单支结点则做对应的操作，若是根结点则结束。

int Delete(BSTree *T,data_type data)
{
    BSTree temp;
    if(data < (*T)->data)//继续在左子树中查找
    {
        return Delete(&(*T)->lchild,data);
    }
    if(data > (*T)->data)//继续在右子树中查找
    {
        return Delete(&(*T)->rchild,data);
    }
    //代码运行到此处，则找到data,即为(*T)->data
    temp = *T;//*T：删除结点地址，T:记录删除结点地址的指针，即为删除结点的父结点的左/右指针
    if((*T)->lchild == NULL)//删除结点的左子树为空，将整个右子树作为树根(此处也包含叶子结点情况)
    {
        (*T) = (*T)->rchild;
        free(temp);
        return 1;
    }
    else if((*T)->rchild == NULL)//删除结点的右子树为空，将整个左子树作为树根
    {
        (*T) = (*T)->lchild;
        free(temp);
        return 1;
    }
    else//删除结点的左右子树都不为空，找左子树的的最大值结点
    {
        if((*T)->lchild->rchild == NULL)//最大值结点为左孩子的情况
        {
            (*T)->data = (*T)->lchild->data;
            Delete(&((*T)->lchild),(*T)->data);
        }
        else        //最大值结点为最深的右孩子结点情况
        {
            BSTree p1,p2;
            p2 = (*T)->lchild;
            p1 = p2->rchild;
            while(p1->rchild != NULL)
            {
                p2 = p1;
                p1 = p1->rchild;
            }
            (*T)->data = p1->data;
            Delete(&(p2->rchild),p1->data);
        }
    }
}

二：二叉搜索树完整代码（C语言）

#include <stdio.h>
#include <stdlib.h>
#include <conio.h>

typedef int data_type;

typedef struct bst
{
    data_type data;
    struct bst *lchild,*rchild;
}BSNode,*BSTree;

BSTree Find(BSTree T,data_type data,BSTree *target) //查找函数,并返回父亲结点地址
{
    if(T == NULL)//二叉树为空
    {
        *target = NULL;
        return NULL;
    }
    else if(T->data == data)//树根即为要查找的结点
    {
        *target = T;
        return NULL;
    }
    else
    {
        while(T)
        {
            if(T->lchild && T->lchild->data == data)
            {
                *target = T->lchild;
                return T;
            }
            if(T->rchild && T->rchild->data == data)
            {
                *target = T->rchild;
                return T;
            }
            if(data > T->data)
            {
                T = T->rchild;
            }
            if(data < T->data)
            {
                T = T->lchild;
            }
        }
        return NULL;
    }
}

int Insert(BSTree *T,data_type data)//插入数据
{
    BSTree newnode,p;
    newnode = (BSTree)malloc(sizeof(BSNode));
    newnode->lchild = newnode->rchild = NULL;
    newnode->data = data;
    if(*T == NULL)
    {
        *T = newnode;
    }
    else
    {
        p = *T;
        while(1)
        {
            if(data == p->data)
            {
                return 0;//数值已存在，不能插入
            }
            else if(data > p->data)
            {
                if(p->rchild == NULL)//右孩子为空，插入
                {
                    p->rchild = newnode;
                    return 1;
                }
                else        //继续向下找
                {
                    p = p->rchild;
                }
            }
            else
            {
                if(p->lchild == NULL)//左孩子为空，插入
                {
                    p->lchild = newnode;
                    return 1;
                }
                else        //继续向下找
                {
                    p = p->lchild;
                }
            }
        }
    }
}


int Delete1(BSTree *T,data_type data)//删除
{
    BSTree fa,target;
    if(*T == NULL)//树为空
    {
        return 0;
    }
    fa = Find(*T,data,&target);//fa为删除结点的父结点，target为删除结点
    if(target->lchild == NULL)    //删除结点左子树为空，右子树不为空的情况(左右子树都为空的情况也适用)
    {
        if(fa == NULL && target->rchild == NULL)//树只存在根结点的情况
        {
            free(*T);
            *T = NULL;
            return 1;
        }
        if(fa->rchild == target)
        {
            fa->rchild = target->rchild;
            free(target);
            return 1;
        }
        if(fa->lchild == target)
        {
            fa->lchild = target->rchild;
            free(target);
            return 1;
        }
    }
    else if(target->rchild == NULL)//删除结点右子树为空，左子树不为空的情况
    {
        if(fa->rchild == target)
        {
            fa->rchild = target->lchild;
            free(target);
            return 1;
        }
        if(fa->lchild == target)
        {
            fa->lchild = target->lchild;
            free(target);
            return 1;
        }
    }
    else    //左右子树都不为空的情况
    {
        if(target->lchild->rchild == NULL)    //孩子结点中最大值结点为target->lchild
        {
            target->data = target->lchild->data;
            return Delete1(&(target->lchild),target->data);
        }
        else        //孩子结点中最大值结点为target->lchild->rchild.....->rchild
        {
            BSTree p1,p2;
            p2 = target->lchild;
            p1 = p2->rchild;
            while(p1->rchild != NULL)//循环找到最大值结点
            {
                p2 = p1;
                p1 = p1->rchild;
            }
            target->data = p1->data;
            return Delete1(&(p2->rchild),p1->data);
        }
    }
}


//a：删除叶子结点，只要将其双亲结点链接到它的指针置空即可。
//b：删除单支结点，只要将其后继指针链接到它所在的链接位置即可
//c：删除双支结点，一般采用的方法是首先把它的中序前驱结点的值赋给该结点的值域，
//然后再删除它的中序前驱结点，若它的中序前驱结点还是双支结点，继续对其做同样的操作，
//若是叶子结点或单支结点则做对应的操作，若是根结点则结束。

int Delete(BSTree *T,data_type data)
{
    BSTree temp;
    if(data < (*T)->data)//继续在左子树中查找
    {
        return Delete(&(*T)->lchild,data);
    }
    if(data > (*T)->data)//继续在右子树中查找
    {
        return Delete(&(*T)->rchild,data);
    }
    //代码运行到此处，则找到data,即为(*T)->data
    temp = *T;//*T：删除结点地址，T:记录删除结点地址的指针，即为删除结点的父结点的左/右指针
    if((*T)->lchild == NULL)//删除结点的左子树为空，将整个右子树作为树根(此处也包含叶子结点情况)
    {
        (*T) = (*T)->rchild;
        free(temp);
        return 1;
    }
    else if((*T)->rchild == NULL)//删除结点的右子树为空，将整个左子树作为树根
    {
        (*T) = (*T)->lchild;
        free(temp);
        return 1;
    }
    else//删除结点的左右子树都不为空，找左子树的的最大值结点
    {
        if((*T)->lchild->rchild == NULL)//最大值结点为左孩子的情况
        {
            (*T)->data = (*T)->lchild->data;
            Delete(&((*T)->lchild),(*T)->data);
        }
        else        //最大值结点为最深的右孩子结点情况
        {
            BSTree p1,p2;
            p2 = (*T)->lchild;
            p1 = p2->rchild;
            while(p1->rchild != NULL)
            {
                p2 = p1;
                p1 = p1->rchild;
            }
            (*T)->data = p1->data;
            Delete(&(p2->rchild),p1->data);
        }
    }
}


void CreateBSTree(BSTree *T)//创建二叉树，调用插入算法创建
{
    data_type data;
    char ch;
    printf("请输入要创建的二叉搜索树的数据(数据之间用空格隔开,输入完毕按回车)：");
    do
    {
        scanf("%d",&data);
        ch = getchar();
        Insert(T,data);
    }
    while (ch != 10);
}

void Inorder(BSTree T)
{
    if(T)
    {
        Inorder(T->lchild);
        printf("%d ",T->data);
        Inorder(T->rchild);
    }
}


int main()
{
    BSTree T,fa,target;
    T = NULL;
    CreateBSTree(&T);
    Inorder(T);
    int select;
    data_type data;
    while(1)
    {
        printf("1.插入  2.删除 3.中序遍历
");
        scanf("%d",&select);
        if(select == 1)
        {
            printf("请输入要插入的数据：");
            scanf("%d",&data);
            Insert(&T,data);
            Inorder(T);
            getch();
        }
        else if(select == 2)
        {
            printf("删除数据：");
            scanf("%d",&data);
            Delete1(&T,data);
            Inorder(T);
            getch();
        }
        else if(select == 3)
        {
            Inorder(T);
            getch();
        }
    }            
    return 0;
}
/* 50 30 80 20 40 90 35 85 32 88*/