图论之杀人游戏

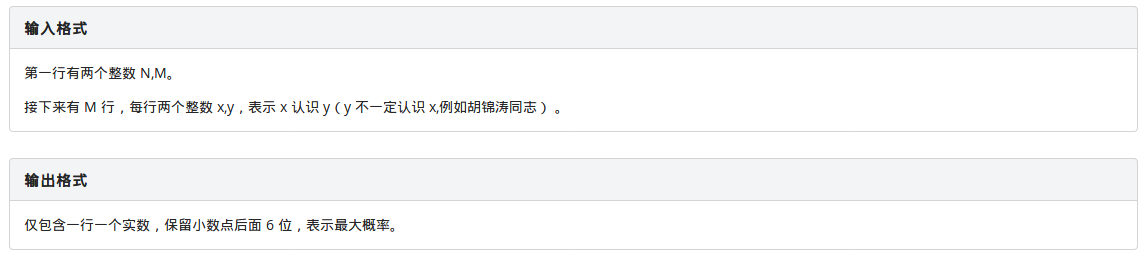
题目

思路

对于一张图来说，我们将其分为链（包括带环链）和环

• 对于链，从链顶（入度为0）开始dfs记录链的个数及大小，注意，大小为1的单点也包括在其中了;
• 处理完链后，对于单个的环来说，所有的点的入度都不为0，所以在处理完链之后还没有处理的就是环了，再dfs一下就ok了;
  显然，对于每一个链状结构（或者环状结构）只需要减去一次链首（或环中任意一个点）是杀手的概率就可以了。
  接下来来考虑单点情况
• 对于单点来说，如果将其他的点都查询完了，最后剩下一个单点，那么这个点是不需要查询的;
• 但是在上面第一种情况下，每一个单点都被考虑了一次，实际对于n个单点，我们只需要考虑n-1次，所以对于存在单点的图，我们把最后一个单点的情况加回来;
  结束了？？？然而并没有
  

对于上面情况，如果我们正向遍历和反向遍历结果是不一样的

• 正向，图中没有单点，一条链和一个带环链
• 反向，图中有一个单点，一个带环链，

所以我们需要正向反向都遍历一遍，取最后概率最大值

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=1000000+10;
const int maxm=300000;
int head[maxn],ver[maxm],Next[maxm],tot,cnt;
void add(int x,int y){
	ver[++tot]=y,Next[tot]=head[x],head[x]=tot;
}
int siz[maxn];
int rd[maxn];
bool vis[maxn];
int n,m;
void dfs(int x){//dfs求每个链状结构或者环状结构的大小
	vis[x]=1;
	siz[cnt]++;
	for(int i=head[x];i;i=Next[i]){
		if(!vis[ver[i]])dfs(ver[i]);
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1,x,y;i<=m;i++){
		scanf("%d%d",&x,&y);
		add(x,y);
		rd[y]++;//记录入度
	}
	int one=0;//记录单点个数
	double ans=1;
	for(int i=1;i<=n;i++){//正向遍历处理链
		if(!vis[i]&&rd[i]==0){
			cnt++;
			dfs(i);
			ans-=(1.0/n);//每增加一个链状结构，就相应减去链首为杀手的概率
			if(siz[cnt]==1)one++;
		}
	}
	for(int i=1;i<=n;i++){//正向遍历处理环
		if(!vis[i]){
			cnt++;
			dfs(i);
			ans-=(1.0/n);
		}
	}
	if(one)ans+=(1.0/n);//如果存在单点，把多减去的加上
	/*====================接下来反向遍历=========================*/
	memset(siz,0,sizeof(siz));
	memset(vis,0,sizeof(vis));
	int one2=0;double ans2=1;
	for(int i=n;i>=1;i--){
		if(!vis[i]&&rd[i]==0){
			cnt++;
			dfs(i);
			ans2-=(1.0/n);
			if(siz[cnt]==1)one++;
		}
	}
	for(int i=n;i>=1;i--){
		if(!vis[i]){
			cnt++;
			dfs(i);
			ans2-=(1.0/n);
		}
	}
	if(one2)ans2+=(1.0/n);
	printf("%.6lf
",max(ans,ans2));//取最大值
}