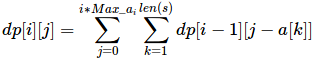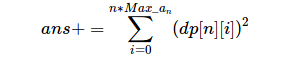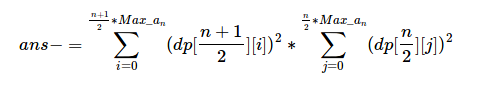计数DP之数字

Descrption

 * 一个数字被称为好数字当他满足下列条件：
 * 它有 2∗n个数位，n 是正整数（允许有前导 0）。
 * 构成它的每个数字都在给定的数字集合 S中。
 * 它前 n位之和与后 n 位之和相等或者它奇数位之和与偶数位之和相等。

• 例如对于 n=2,S={1,2}，合法的好数字有 1111,1122,1212,1221,2112,2121,2211,2222 这样 8种。
• 已知 n，求合法的好数字的个数 mod 999983。

Input

第一行一个数 n。接下来一个长度不超过 10的字符串，表示给定的数字集合（不存在重复的数字）。

Output

一行，一个整数表示合法的好数字的个数 mod 999983。

Sample Input

  2
  0987654321

Sample Output

  1240

思路

• 维护dp数组dp[i][j]表示i个数位和为j的种类数，那么易得
  
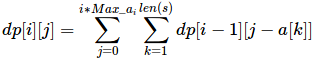
• 前n和后n和相同的方案数和奇数位和与偶数位和相等的方案数是一样的，只不过排列顺序不同，
  前 n 与后 n 和相同：将和相等，且个数为 n 的两个序列拼在一起即可，方案数为：
  
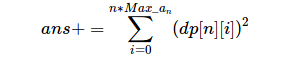
• 显然存在两种情况都符合的方案，接下来是去重操作，
  前n个中奇数和为s1，偶数和为s2-->后n个中奇数和为s2，偶数和为s1
  对于n为奇数，后n个数中的奇数位为总数位的偶数位，s1（左）=s1（右），s2（左）=s2（右）
  对于n为偶数，不会影响
  减去重复的情况
  

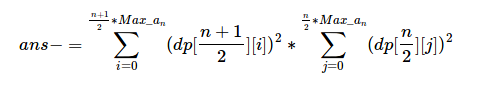
代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e3+5,mod=999983;
int dp[maxn][9*maxn];
int n,a[11];
signed main(){
	char s[11];scanf("%lld%s",&n,s+1);
	a[0]=strlen(s+1);
	for(int i=1;i<=a[0];i++){
		a[i]=s[i]-48;
	}
	dp[0][0]=1;
	for(int i=1;i<=n;i++){
		for(int j=0;j<=i*9;j++){
			for(int k=1;k<=a[0];k++){
				if(j>=a[k]){
					dp[i][j]=(dp[i][j]+dp[i-1][j-a[k]])%mod;
				}
			}
		}
	}
	int ans=0;
	for(int i=0;i<=9*n;i++){
		ans=(ans+(2*dp[n][i]*dp[n][i])%mod)%mod;
	}
	int len1=(n+1)/2,len2=n/2;
	int ans1=0,ans2=0;
	for(int i=0;i<=9*len1;i++){
		ans1=(ans1+(dp[len1][i]*dp[len1][i])%mod)%mod;
	}
	for(int i=0;i<=9*len2;i++){
		ans2=(ans2+(dp[len2][i]*dp[len2][i])%mod)%mod;
	}
	ans=(ans-ans1*ans2%mod+mod)%mod;
	printf("%lld
",ans);
}