状压DP之吃奶酪

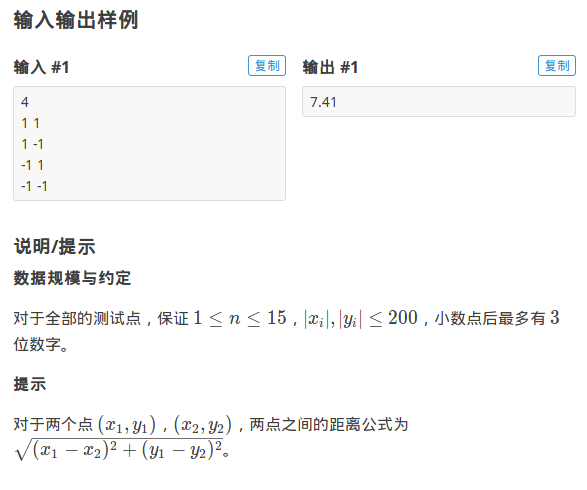
题目

传送们

思路

1≤n≤15，妥妥的状压，数据这么小，
这道题的状压思路还是很好想的，我们定义f[i][s]代表以i为起点，吃掉状态为s的奶酪所需要跑的最短距离，那么显然，我们先枚举状态s，然后枚举出发点i，判断合法性（s是否包括i），然后枚举所需加入的起点j（s如果包含j则跳过），然后就可以很自然的推出转移方程

f[i][s]=min(f[i][s],f[j][s-(1<<(i-1))]+dis(i,j));

最后不要忘记加上出发点（0，0）就行了。

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=1<<16;
double f[20][maxn];
double x[20],y[20];
double dis(int i,int j){
	double ans=0;
	ans=sqrt((double)((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j])));
	return ans;
}
int main(){
	int n;scanf("%d",&n);
	for(int i=1;i<=n;i++){
		cin>>x[i]>>y[i];
	}
	int lim=1<<n;
	memset(f,0x7f,sizeof(f));
	for(int i=1;i<=n;i++){
		f[i][1<<(i-1)]=0;
	}
	for(int s=0;s<lim;s++){
		for(int i=1;i<=n;i++){
			if((s&(1<<(i-1)))==0)continue;
			for(int j=1;j<=n;j++){
				if(((s&(1<<(j-1)))==0)||i==j)continue;
				f[i][s]=min(f[i][s],f[j][s-(1<<(i-1))]+dis(i,j));
			}
		}
	}	
    double ans=-1;
    for(int i=1;i<=n;i++){
       double s=f[i][(1<<n)-1]+dis(i,0);
        if(ans==-1||ans>s) ans=s;
    }
    printf("%.2lf
",ans);
    return 0;
}