最近在参加大数据的暑期培训,记录一下学习的东西。
引言
懒惰学习法:简单的存储数据,并且一直等待,直到给定一个检验数据,才进行范化,以便根据与存储的训练元组的相似性对该检验数据进行分类。懒惰学习法在 训练元组的时候只做少量的工作,而在进行分类或者数值预测时做更多的工作。由于懒惰学习法存储训练元组或实例,也被称为基于实例的学习法。
K-近邻算法是简单的分类与回归方法,属于懒惰学习法。
K-近邻算法的基本做法:给定一个训练数据集,在训练数据集中找到与未知实例最邻近的K个训练集中的实例,这K个实例的多数属于某个类,就把该未知实例分类到这个类中。
算法描述:
1、数据标准化
2、计算测试数据与各个训练数据之间的距离
3、按照距离的递增关系进行排序
4、选取距离最小的K个点
5、确定前K个点所在类别出现的频率
6、返回前K个点中出现频率最高的类别作为测试数据的预测分类
K近邻算法的三个基本要素:k值的选择,距离度量,分类决策规则
一、数据标准化
作用:防止某一属性权重过大
比如说坐标点 x,y。 x的范围是【0,1】,但y的范围却是【100,1000】,在进行距离的计算的时候y的权重比x的权重大。
这里就用最简单的一种标准化方法:
Min-max标准化: x‘ = (x -min)/(max-min)
举个例子:
x数据集为[1, 2, 3, 5], 则min=1, max=5
1 : (1-min) / (max-min) = 0
2 : (2-min) / (max-min) = 0.25
3 : (3-min) / (max-min) = 0.5
5 : (5 -min) / (max-min) = 1
则x数据集被更新为 x'[0, 0.25, 0.5, 1]
Min-max方法 x‘ 被标准化在[0,1]区间中
二、距离度量
计算两点间的距离:计算距离有欧式距离,曼哈顿距离等等, 一般采用欧式距离。
欧式距离公式 :
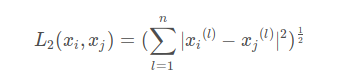
就比如(x1, y1)和 (x2, y2)的距离为

多维也是一样的,对应坐标相减,平方后,求和,再求根号
曼哈顿距离:
曼哈顿距离公式:
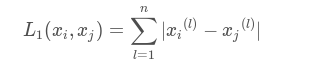
点(x1, y1)和(x2, y2)的曼哈顿距离为: |x1-x2| + |y1-y2|
多维为对应坐标相减的绝对值求和
根据需求选择不同的距离度量
三、确定K值
k值的选择会对k近邻法的结果有很大的影响,k值较小意味着只有与输入实例较近的训练实例才会对预测结果起作用,但容易发生过拟合;如果k值较大,优点是可以减少学习的估计误差,缺点是学习的近似值误差增大,这时与输入实例较远的训练实例也会起预测作用,使预测发生错误。在实际应用中,k值一般选择一个较小的数值,采用交叉验证的方法来选择最优的k值。
四、分类决策规则
分类决策规则是只按照什么规则确定当前实例属于哪一类。
k近邻算法中,分类决策规则往往是多数表决,即由输入实例的K个最邻近的训练实例中的多数类决定输入实例的类别。
五、优缺点
优点:简单,易于理解,无需建模与训练,易于实现;适合对稀有事件进行分类。
缺点:懒惰算法,内存开销大,对测试样本分类时计算量也比较大,性能较低;可解释性差,无法给出决策树那样的规则。