1. 马尔可夫模型的几类子模型
马尔科夫链(Markov Chain),了解机器学习的也都知道隐马尔可夫模型(Hidden Markov Model,HMM)。它们具有的一个共同性质就是马尔可夫性(无后效性),也就是指系统的下个状态只与当前状态信息有关,而与更早之前的状态无关。
马尔可夫决策过程(Markov Decision Process, MDP)也具有马尔可夫性,与上面不同的是MDP考虑了动作,即系统下个状态不仅和当前的状态有关,也和当前采取的动作有关。还是举下棋的例子,当我们在某个局面(状态s)走了一步(动作a),这时对手的选择(导致下个状态s’)我们是不能确定的,但是他的选择只和s和a有关,而不用考虑更早之前的状态和动作,即s’是根据s和a随机生成的。
我们用一个二维表格表示一下,各种马尔可夫子模型的关系就很清楚了:
| 不考虑动作 | 考虑动作 | |
| 状态完全可见 | 马尔科夫链(MC) | 马尔可夫决策过程(MDP) |
| 状态不完全可见 | 隐马尔可夫模型(HMM) | 不完全可观察马尔可夫决策过程(POMDP) |
2. 马尔可夫决策过程
一个马尔可夫决策过程由一个四元组构成M = (S, A, Psa, R ) [注1]
- S: 表示状态集(states),有s∈S,si表示第i步的状态。
- A:表示一组动作(actions),有a∈A,ai表示第i步的动作。
- Psa: 表示状态转移概率。Psa 表示的是在当前s ∈ S状态下,经过a ∈ A作用后,会转移到的其他状态的概率分布情况。比如,在状态s下执行动作a,转移到s'的概率可以表示为p(s'|s,a),也可以说s‘的分布服从Psa。
- R: S×A€ℝ ,R是回报函数(reward function)。有些回报函数状态S的函数,可以简化为R: S € ℝ。如果一组(s,a)转移到了下个状态s',那么回报函数可记为r(s'|s, a)。如果(s,a)对应的下个状态s'是唯一的,那么回报函数也可以记为r(s,a)。(这里分为确定性和不确定。确定性的回报,即当在s下执行a时,下个状态s’是确定的;而不确定性的回报是指当在s下执行a时,下个状态s’是不确定的,即带概率的,这时我们需要用确定的期望值来代替不确定,即 E(r(s'|s, a)) = Σs1[p(s1|s,a) * r(s1|s,a)] )
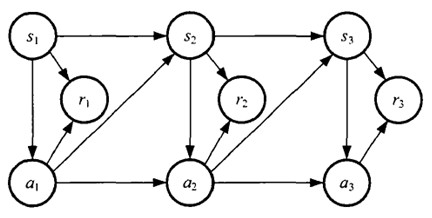
MDP 的动态过程如下:某个agent(智能体,也翻译成代理、学习者)的初始状态为s0,然后从 A 中挑选一个动作a0执行,执行后,agent 按Psa概率随机转移到了下一个s1状态,s1∈ Ps0a0。然后再执行一个动作a1,就转移到了s2,接下来再执行a2…,我们可以用下面的图表示状态转移的过程。
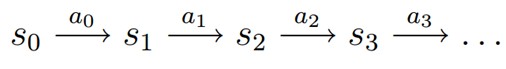
如果回报r是根据状态s和动作a得到的,则MDP还可以表示成下图: