华盛顿大学 《机器学习》 笔记。
knn
k-nearest-neighbors : k近邻法
给定一个 数据集,对于查询的实例,在数据集中找到与这个实例最邻近的k个实例,然后再根据k个最邻近点预测查询实例的类别。
《统计学习方法》中这样描述的:


K近邻模型是基于训练数据集 对 特征空间的一个划分。
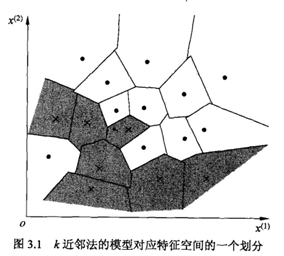
当k =1 ,为一种特殊情况,称为最邻近法。
Knn算法实现的三个重要问题: 距离度量选择、k值选择,分类决策方法。
1. 距离度量选择
常用的距离度量有欧式距离、曼哈顿距离等。

《统计学习方法》中对距离度量总结:

2. K值选择
K过小,预测结果对邻近的实例点十分敏感,容易发生过拟合。
K过大,估计误差(estimation error)可以减小,但近似误差(approximation error)增大,与实例点隔得很远的训练实例也会对预测起作用。
k值一般由交叉验证(cross validation)决定。
3.分类决策方法
即找到k个最邻近点后,如何得出最后的输出结果。对于分类问题,往往采用多数表决。
《统计学习方法》:

kd树
实现knn算法时,一个主要的问题是如何对数据集快速搜索。其中,暴力搜索复杂度O(Nlogk),使用特殊的数据结构可以提高搜索效率。
Kd树是二叉树,表示对k维空间(k是特征的数量)的一个划分。Kd树是一种存储数据集的方式,以便于进行快速搜索。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分,构造成一系列的k维超矩形区域,kd树的每个结点对应于一个k维超矩形区域(《统计学习方法》)。
Kd树的构造方式:以2维空间为例(2个特征)。
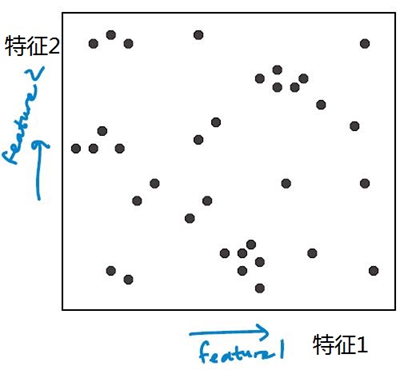
输入数据集,输出kd树。特征为x = (x[1], x[2])
开始:根节点为包含整个数据集的矩形区域(如下图所示)。以 feature 1 为切割特征,将整个区域切割成两个子空间,生成两个子节点。
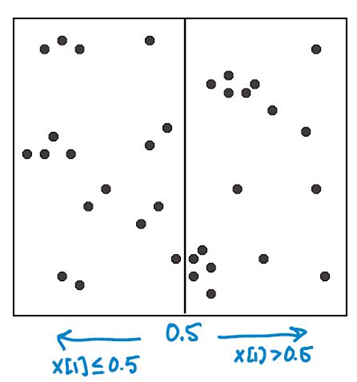
对每个子区域递归,重复切分。直到子区域中包含的数据点少于设定的临界值为止。
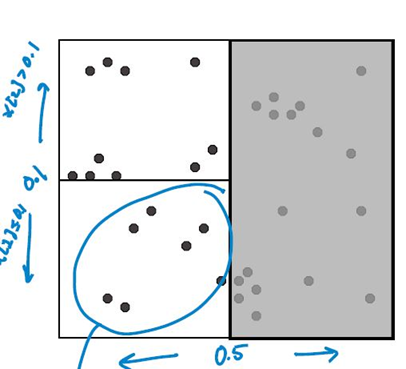
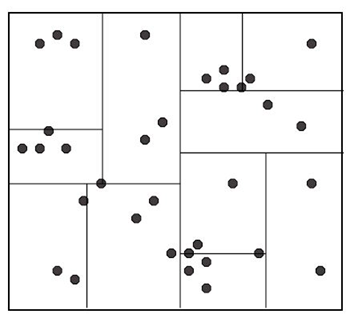
给定一个查询点,搜素其近邻点的方法:
从根节点出发,根据查询点的特征值找到包含查询点的叶子节点,在叶子节点里搜索。
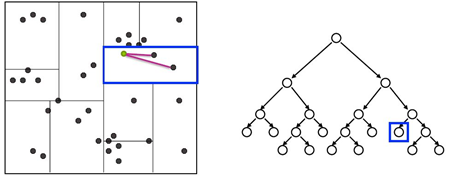
之后再回溯到父节点,在父节点的其他子节点中搜索,这样搜索范围被限制在数据集空间的局部区域,提高搜索效率。
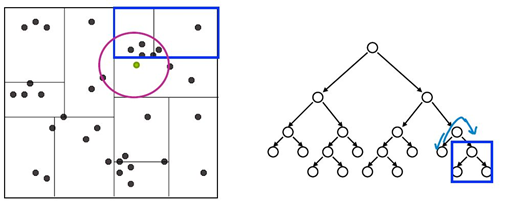
复杂度:
构造二叉树的复杂度:
size: 如果每个叶节点只包含1个数据点,一共2N-1个节点。
depth: O(log N)
构造时间:O(N log N)
查询复杂度:
找到叶子节点: O ( log N)
回溯到父节点以及移动到另一个子节点搜素最大花费: O(N)
复杂度 O ( log N) --> O(N)
(N 为训练集数据点总数)
注:通过一些剪枝和优化,查询时间复杂度非常接近O(logN),kd树适用于低维空间(特征数较少)的情况,维度较高时接近暴力搜索方法。
对于高维情况,kd树就不是很适用了,可以使用 LSH(locality sensitive hashing )。
LSH
LSH(locality sensitive hashing ),LSH通过将数据集的所有数据点随机分区到不同的分箱(bin)来执行有效的邻域搜索。
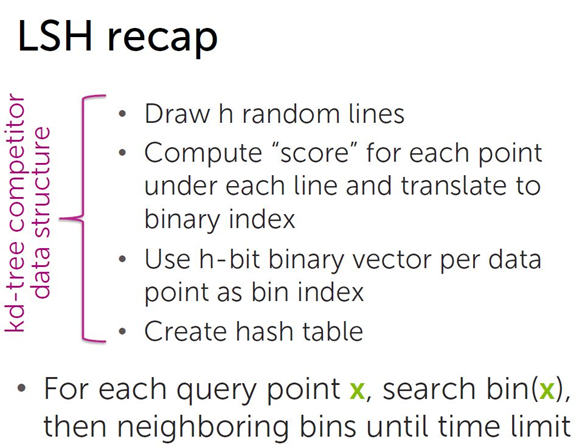
实现过程:
将数据集空间划分成若干个分箱(bin)。
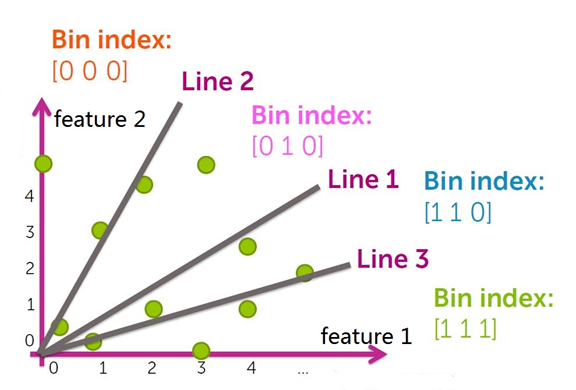
根据分箱的划分情况,每个分箱编码(bin index)都可以用一个二进制串表示,即得到所有分箱的hash值。
被划分到各个分箱中的数据点用分箱(bin)的 bin index 表示,即相似的数据点(映射到同一个分箱(bin)的数据点)所映射的hash值相同,以此得到数据集中所有点的哈希值,构造哈希表。
对于每个查询点 x ,先在相应bin index的分箱中搜索,然后搜索邻近的分箱( bin index相差一位的分箱, 相差两位的分箱 …)。
随机二元投影LSH实现:
模型构建:
# 输入:
# data_matrix: 数据集矩阵 ,其中data_matrix[i, j]表示数据点i的特征j的值.
# k: bin index 位数
# 输出:
# random_vectors: 用于随机划分数据集的随机向量组
# index_bits, bin_indices: 分箱编号(bin index),bin_indices[i]:表示数据点i划分到编号为 bin_indices[i]的分箱中
# lsh_bin: 每个分箱中的数据点,lsh_bin[i]为一个list,表示编号为 i 的分箱中的数据点的序号
def train_lsh_model(data_matrix, k):
# 第一步:用标准高斯分布生成随机向量组
# 其中,随机向量的维度 dim 为数据集的大小
# bin index为 k-bit的二进制串,每个向量可用于计算bin index中的一位,随机向量数量为 k 。
dim = data_matrix.shape[1]
num_vector = k
random_vectors = np.random.randn(dim, num_vector)
# 第二步:将所有数据点划分到分箱中,并计算分箱编号(bin index)
index_bits = data_matrix.dot (random_vectors) >= 0
# bin index为k-bit的二进制串,为了方便表示,用对应的整数代替。
powers_of_two = (1 << np.arange(num_vector-1, -1, -1))
bin_indices = index_bits.dot(powers_of_two)
# 更新每个分箱中的数据点list
lsh_bin = {}
for data_index, bin_index in enumerate(bin_indices):
if bin_index not in table:
lsh_bin[bin_index] = []
lsh_bin[bin_index].append(data_index) #data index为 数据点序号
model = {'bin_indices': bin_indices,
'index_bits': index_bits ,
'lsh_bin': lsh_bin,
'random_vectors': random_vectors}
return model
使用LSH得到搜索邻域:
# 得到待搜索的数据点集
# 输入: 查询数据点x, LSH模型,搜索范围(bin index最多相差几位)
# 输出: 待搜索的数据点集candidate_set
def lsh_search_candidate_set(query_id, lsh_model, search_radius):
query_bin_bits = lsh_model['index_bits'][query_id]
lsh_bin = lsh_model['lsh_bin']
num_vector = len(query_bin_bits)
powers_of_two = 1 << np.arange(num_vector-1, -1, -1)
candidate_set = set()
for r in xrange(search_radius+1):
# 罗列所有翻转的位数(combinations:全排列)
for different_bits in combinations(range(num_vector), r):
# 翻转bin index相应的位数,得到邻近分箱的编号
alternate_bits = copy(query_bin_bits)
for i in different_bits:
alternate_bits[i] = (query_bin_bits[i] == False)
nearby_bin_index = alternate_bits.dot(powers_of_two)
# 将邻近分箱中的数据点加入 candidate_set
if nearby_bin in table:
candidate_set.update(tuple(lsh_bin[nearby_bin]))
return candidate_set