hihoCoder #1388 : Periodic Signal ( 2016 acm 北京网络赛 F题)

时间限制:5000ms

单点时限:5000ms

内存限制:256MB

描述

Profess X is an expert in signal processing. He has a device which can send a particular 1 second signal repeatedly. The signal is A_{0 ...} A_n-1 under n Hz sampling.

One day, the device fell on the ground accidentally. Profess X wanted to check whether the device can still work properly. So he ran another n Hz sampling to the fallen device and got B_{0 ...} B_n-1.

To compare two periodic signals, Profess X define the DIFFERENCE of signal A and B as follow:

You may assume that two signals are the same if their DIFFERENCE is small enough.
Profess X is too busy to calculate this value. So the calculation is on you.

题解：

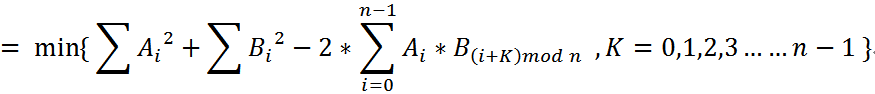
A[]的平方和 与 B[]的平方和可以直接求出。所以只要求出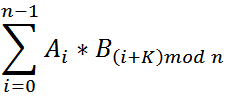的最大值即可得到答案。

即求A[]与B[]的循环卷积。 FFT求解。

注意由于数据较大，FFT会出现精度问题。最后结果会有浮点精度误差，但是由结果得到的 k 是正确的，所以一个无赖的办法是根据FFT 的结果求 K，然后再自己算一遍得到最后答案。

注：题解的标准做法是找两个 10910^910​9​​ 左右模数 NTT 后 CRT 。

#include <algorithm>
#include <cstring>
#include <string.h>
#include <iostream>
#include <list>
#include <map>
#include <set>
#include <stack>
#include <string>
#include <utility>
#include <vector>
#include <cstdio>
#include <cmath>

#define LL long long
#define N 60005
#define INF 0x3ffffff

using namespace std;

const long double PI = acos(-1.0);


struct Complex // 复数
{
    long double r,i;
    Complex(long double _r = 0,long double _i = 0)
    {
        r = _r; i = _i;
    }
    Complex operator +(const Complex &b)
    {
        return Complex(r+b.r,i+b.i);
    }
    Complex operator -(const Complex &b)
    {
        return Complex(r-b.r,i-b.i);
    }
    Complex operator *(const Complex &b)
    {
        return Complex(r*b.r-i*b.i,r*b.i+i*b.r);
    }
};

void change(Complex y[],int len) // 二进制平摊反转置换 O(logn)
{
    int i,j,k;
    for(i = 1, j = len/2;i < len-1;i++)
    {
        if(i < j)swap(y[i],y[j]);
        k = len/2;
        while( j >= k)
        {
            j -= k;
            k /= 2;
        }
        if(j < k)j += k;
    }
}
void fft(Complex y[],int len,int on) //DFT和FFT
{
    change(y,len);
    for(int h = 2;h <= len;h <<= 1)
    {
        Complex wn(cos(-on*2*PI/h),sin(-on*2*PI/h));
        for(int j = 0;j < len;j += h)
        {
            Complex w(1,0);
            for(int k = j;k < j+h/2;k++)
            {
                Complex u = y[k];
                Complex t = w*y[k+h/2];
                y[k] = u+t;
                y[k+h/2] = u-t;
                w = w*wn;
            }
        }
    }
    if(on == -1)
        for(int i = 0;i < len;i++)
            y[i].r /= len;
}

const int MAXN = 240040;

Complex x1[MAXN],x2[MAXN];
LL a[MAXN/4],b[MAXN/4];                //原数组
long long num[MAXN];     //FFT结果
void init(){
     memset(num,0,sizeof(num));
     memset(x1,0,sizeof(x1));
     memset(x2,0,sizeof(x2));
}

int main()
{
    int T;
    scanf("%d",&T);
    LL suma,sumb;
    while(T--)
        {
            int n;
             suma=0;sumb=0;
            init();
            scanf("%d",&n);
             for(int i = 0;i < n;i++) {scanf("%lld",&a[i]);suma+=a[i]*a[i];}
             for(int i = 0;i < n;i++) {scanf("%lld",&b[i]);sumb+=b[i]*b[i];}
            int len = 1;
            while( len < 2*n ) len <<= 1;
             for(int i = 0;i < n;i++){
                x1[i] = Complex(a[i],0);
            }
             for(int i = 0;i < n;i++){
                x2[i] = Complex(b[n-i-1],0);
            }
      //      for(int i=n;i<len;i++) x1[i]=Complex(0,0);
            fft(x1,len,1);fft(x2,len,1);
            for(int i = 0;i < len;i++){
                x1[i] = x1[i]*x2[i];
            }
            fft(x1,len,-1);
            for(int i = 0;i < len;i++){
                num[i] = (LL)(x1[i].r+0.5);
            }
          //  for(int i = 0;i < len;i++) cout<<num[i]<<endl;
          LL ret=num[n-1];
          int flag=0;
         // cout<<ret<<endl;
          for(int i=0;i<n-2;i++) {
            //    cout<<num[i]+num[i+n]<<endl;
            if(ret<num[i]+num[i+n])
                {ret=num[i]+num[i+n]; flag=n-1-i;}
                  //注意，此时得到的ret会有很小的浮点精度误差,
                //flag表示k,这个是正确的
          }
          ret=0;
          for(int i=0;i<n;i++){
            ret+=a[i]*b[(i+flag)%n]; //重新算一遍得到最后答案
          }
          LL ans=suma+sumb-2*ret;
          cout<< ans<<endl;
        }
    return 0;
}