通过上篇文章,大家已经能够清楚的了解到treeMap插入结点的过程,那么本篇文章就来分析下TreeMap删除一个结点时,内部数据结构发生了怎样的变化。
TreeMap删除某个结点的源码分析

1 /** 2 * 删除节点,并平衡红黑树的操作 3 * 4 * @Param Entry<K,V> p 要删除的节点Entry 5 */ 6 private void deleteEntry(Entry<K,V> p) { 7 modCount++; 8 size--; //节点总数-1 9 10 if (p.left != null && p.right != null) { //当前要删除的节点左右子节点都不为空 11 Entry<K,V> s = successor(p); //找到一个待删除节点的继承者节点s 12 //将指向s节点,后续所有对p的节点判断其实都是对s节点判断 13 p.key = s.key; 14 p.value = s.value; 15 p = s; 16 } 17 18 //替代节点选择为当前被删除节点的左子节点(优先)或右子节点 19 Entry<K,V> replacement = (p.left != null ? p.left : p.right); 20 21 if (replacement != null) { //替代节点(被删除节点的子节点)不为空 22 23 replacement.parent = p.parent; //将替代节点的父节点指向被删除节点的父节点 24 if (p.parent == null) //如果被删除节点的父节点为null (即被删除的节点就是树的根节点,且根节点下面还有其他节点) 25 root = replacement; //将根节点设置为替换节点 26 else if (p == p.parent.left) //如果原先被删除节点是左子树 插入 27 p.parent.left = replacement; //则将替换节点也保持左子树插入(将替换节点与被删除节点的父节点左子节点建立引用) 28 else //如果原先被删除节点是右子树 插入 29 p.parent.right = replacement; //则将替换节点也保持右子树插入(将替换节点与被删除节点的父节点右子节点建立引用) 30 31 //将被删除节点的左子节点、右子节点、父节点引用全部置为null 32 p.left = p.right = p.parent = null; 33 34 //删除后要执行后续的保证红黑树规则的操作 35 if (p.color == BLACK) //如果被删除节点是黑色的 36 fixAfterDeletion(replacement); //调用删除后修正红黑树规则的方法 37 } else if (p.parent == null) { //被删除节点就是根节点,且整个树中就只有一个根节点的情况 38 root = null; //将根节点置为null(此时整个树中就没有节点了) 39 } else { //被删除节点没有子节点可替代的情况 (被删除节点是叶子节点) 40 if (p.color == BLACK) //如果被删除节点是黑色的 41 fixAfterDeletion(p); //调用删除后修正红黑树规则的方法 42 43 if (p.parent != null) { //如果被删除节点的父节点不为null 44 if (p == p.parent.left) //如果原先被删除节点是左子树 插入 45 p.parent.left = null; //删除节点后将被删除节点的父节点的左子节点置为null 46 else if (p == p.parent.right) //如果原先被删除节点是右子树 插入 47 p.parent.right = null; //删除节点后将被删除节点的父节点的右子节点置为null 48 p.parent = null; //将被删除节点的父节点引用置为null(即将被删除节点从树中移除) 49 } 50 } 51 }
源码逻辑很简单,主要就是分为删除结点有子结点和无子结点,而无子结点又分为删除的是根结点或叶子结点这三种情况
然后如果被删除结点是黑色的,那么要注意下可能继承者和被删除结点的父结点都是红色的情况,此时需要做平衡红黑树的操作。
这里需要注意的方法有两个: 第11行的 successor() 方法 以及 第36行的 fixAfterDeletion() 方法。
分别贴一下这两个方法的源码:
1 /** 2 * 返回被删除节点的继承者节点 3 */ 4 static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) { 5 if (t == null) //如果被删除节点为空,则直接返回null 6 return null; 7 else if (t.right != null) { //如果被删除节点的右子节点不为空 8 Entry<K,V> p = t.right; //将被删除节点的右子节点记录下来 9 while (p.left != null) //从该节点开始循环向下查找左子节点,直至找到叶子节点后返回该叶子节点 10 p = p.left; 11 return p; 12 } else { //如果被删除节点的右子节点为空 13 Entry<K,V> p = t.parent; //将被删除节点的父节点用p变量记录 14 Entry<K,V> ch = t; //被删除节点用ch变量记录 15 while (p != null && ch == p.right) {//从被删除节点开始循环向上查找父节点,直到父节点为空或者父节点没有右子节点,返回该父节点 16 ch = p; 17 p = p.parent; 18 } 19 return p; 20 } 21 }

1 /** 2 * 树删除一个节点后,将其根据红黑树的规则进行修正 3 * @param x 当前删除的节点 4 */ 5 private void fixAfterDeletion(Entry<K,V> x) { 6 //循环遍历,x刚开始为被删除的节点 7 while (x != root && colorOf(x) == BLACK) { //如果当前遍历到的节点不是根节点且为黑色 8 if (x == leftOf(parentOf(x))) { //如果当前遍历到的节点是其父节点的左子节点 9 Entry<K,V> sib = rightOf(parentOf(x)); //将当前遍历到的节点的父节点的右子节点用sib变量保存(即和当前节点平级的另一个节点) 10 11 if (colorOf(sib) == RED) { //如果sib引用的节点是红色的 12 setColor(sib, BLACK); //将sib引用的节点设置为黑色 13 setColor(parentOf(x), RED); //将当前遍历到节点的父节点设置为红色 14 rotateLeft(parentOf(x)); //对当前遍历到节点的父节点进行一次左旋操作 15 sib = rightOf(parentOf(x)); //sib引用的节点变更为旋转后被删除节点的父节点的右子节点 16 } 17 18 if (colorOf(leftOf(sib)) == BLACK && 19 colorOf(rightOf(sib)) == BLACK) { //如果sib引用节点的左、右子节点都是黑色的 20 setColor(sib, RED); //将sib引用的节点设置为红色 21 x = parentOf(x); //下一次遍历的节点变更为当前遍历到节点的父节点 22 } else { //如果sib引用节点的左、右子节点不全是黑色的 23 if (colorOf(rightOf(sib)) == BLACK) { //如果sib引用节点的右子节点是黑色的 24 setColor(leftOf(sib), BLACK); //将sib引用节点的左子节点设置为黑色 25 setColor(sib, RED); //sib引用节点设置为红色 26 rotateRight(sib); //对sib节点进行一次右旋操作 27 sib = rightOf(parentOf(x)); //sib引用的节点变更为当前遍历到的节点的父节点的右子节点 28 } 29 setColor(sib, colorOf(parentOf(x))); //将sib引用节点的颜色设置为 当前遍历到节点的父节点 一样的颜色 30 setColor(parentOf(x), BLACK); //将当前遍历到节点的父节点设置为黑色 31 setColor(rightOf(sib), BLACK); //将sib引用节点的右子节点设置为黑色 32 rotateLeft(parentOf(x)); //对当前遍历到的节点的父节点进行一次左旋操作 33 x = root; //下一次遍历的节点变更为根节点 34 } 35 } else { // 当前遍历到的节点是其父节点的右子节点,和上述情况相似,不再赘述 36 Entry<K,V> sib = leftOf(parentOf(x)); 37 38 if (colorOf(sib) == RED) { 39 setColor(sib, BLACK); 40 setColor(parentOf(x), RED); 41 rotateRight(parentOf(x)); 42 sib = leftOf(parentOf(x)); 43 } 44 45 if (colorOf(rightOf(sib)) == BLACK && 46 colorOf(leftOf(sib)) == BLACK) { 47 setColor(sib, RED); 48 x = parentOf(x); 49 } else { 50 if (colorOf(leftOf(sib)) == BLACK) { 51 setColor(rightOf(sib), BLACK); 52 setColor(sib, RED); 53 rotateLeft(sib); 54 sib = leftOf(parentOf(x)); 55 } 56 setColor(sib, colorOf(parentOf(x))); 57 setColor(parentOf(x), BLACK); 58 setColor(leftOf(sib), BLACK); 59 rotateRight(parentOf(x)); 60 x = root; 61 } 62 } 63 } 64 65 setColor(x, BLACK); 66 }
可能光看这两个方法的源码不太好理解,下面就以删除几个结点的实例,一步一步跟踪下源码看看数据结构到底发生了哪些变化。
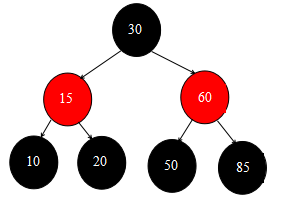
先回顾下上一篇文章插入结点完成后的红黑树状态图:
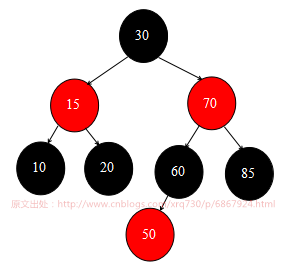
好,那么首先来删除根结点30。因为30结点既有左子结点,又有右子结点,所以在deleteEntry()方法中需要调用successor() 方法寻找继承者结点。
查看successor() 方法源码,可以发现会走第7行的 else if 逻辑,然后从70结点开始循环查找左子结点,直到找到叶子结点50为止,所以最终的继承者结点就是50,下面的三行代码会将根结点30的key-value变为继承者的key-value,所以现在根结点为50,黑色。
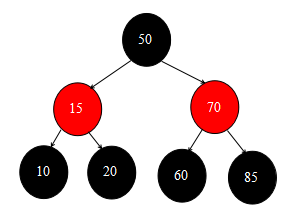
然后下一行会取得replacement变量,因为现在p=s了,即这里的p.left实际判断的是叶子结点50是否有左子结点,很显然叶子结点50既没有左子结点也没有右子结点,所以最后replacement = null。
而叶子结点50是有父结点的,所以不会走 else if (p.parent == null) 分支,而是走下面的else{}分支。叶子结点50目前是红色的,所以不需要做平衡红黑树的操作。
再往下,很显然叶子结点50是有父结点的,所以会走 if (p.parent != null) 的分支,而这个分支里面又是一个if-else分支,这里判断的是当前结点是左子树插入还是右子树插入,叶子结点50很明显是左子树插入,所以会执行 p.parent.left = null 这行代码,即把叶子结点50给删除掉了。
全部过程执行完后,红黑树当前的状态图如下所示:
经过一次删除操作后,童鞋们是否对这两个方法有点印象了呢?不过这次删除30结点我们找到的继承者结点50是红色的,所以没有走修正红黑树平衡的操作。那么下面就再删除一个结点,让它进行平衡红黑树的操作。
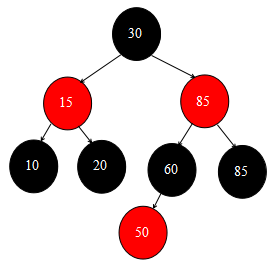
还是以最原始的红黑树状态图为基准,这次我们来删除结点70。70也需要寻找继承者结点,因为70有右子结点,所以会走 else if (t.right != null) 这个分支逻辑,然后指针移动到85结点,而又因为85没有左子结点,所以不符合下面的 while (p.left != null)循环条件,方法结束,最后选择的继承者结点就是85结点。
然后和上面一样,会走三行代码,将70结点变更为85结点,然后将指针指向85结点。很显然85结点既没有左子结点也没有右子结点,所以replacement = null。然后85结点是有父结点的,所以和上面一样走的是else{}分支。
注意,这里和上面的不同之处在于,目前指针是指向85这个节点的,而这个节点是黑色的,所以在else{}分支里的 if (p.color == BLACK) 为true,则会调用 fixAfterDeletion(p) 这个方法进行红黑树的修正操作。
在调用修正操作之前,红黑树的状态是这样的:
好,接下来我们看一下具体的修正操作干了哪些事情。
首先此时指针指向的黑色85结点是满足 while (x != root && colorOf(x) == BLACK) 这个循环条件的,然后这个节点是右子树插入的,所以会走else{}分支。
然后下一步的sib节点取得是父结点的左子结点,即60结点,而60结点是黑色,所以不会走 if (colorOf(sib) == RED) 这个分支逻辑。
然而60结点的左右子结点都不是黑色的,所以会走下面的else{}分支,并且不会走 else分支中的 if (colorOf(leftOf(sib)) == BLACK) 这个判断,只会从第 56 行的代码开始走
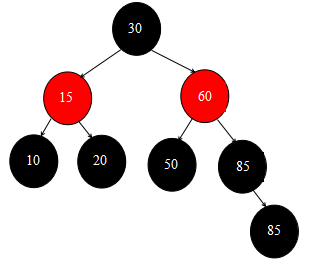
setColor(sib, colorOf(parentOf(x))) 是将60结点的颜色设置为何黑色85结点的父结点(即红色85结点)的颜色,所以此时60结点变为红色。
setColor(parentOf(x), BLACK) 这一行又把红色的85结点设置为了黑色
setColor(leftOf(sib), BLACK) 这一行又将50结点设置成了黑色,此时除了60结点为红色,其余的50、85、85结点都是黑色
rotateRight(parentOf(x)) 这一行以之前为红色的85结点为中心,做一次右旋操作。忘记旋转操作的童鞋看看前面的帖子,就不难理解啦。
然后将指针移动回根结点,并设置根结点为黑色,此时整个修正红黑树操作就结束了。此时红黑树状态图如下所示:
注意:不要忘记再回到之前的deleteEntry方法中去,只是走完了修正红黑树的方法,但整个删除操作还没全部结束呢!
回到原方法的 if (p.parent != null)分支,此时85结点是有父结点的,所以会走这个分支逻辑,然后85又是右子树插入的,所以会走 else if (p == p.parent.right) 这个分支逻辑
然后这行 p.parent.right = null 会将叶子结点85删除,此时才是真正走完了整个删除节点的操作。此时童鞋们小本本上的红黑树应该是这样的哟:
好了,大家是不是觉得其实红黑树的操作并不是很困难呢?只要肯踏踏实实、一步一步的去仔细分析每一步红黑树是如何变化的就能够轻松得到结果。
最后还有一个删除叶子结点的没有讲,比较简单就让童鞋们自己去研究实践吧!
在这里放上两张状态图,以便童鞋们进行验证(图中的状态是以删除叶子结点85为例所得到的结果):
1.进行红黑树修正操作之后的状态图:
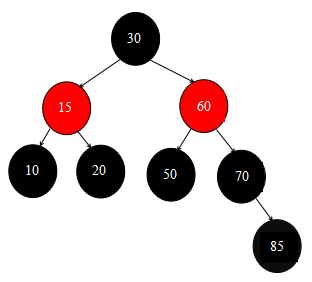
2.删除叶子结点85操作全部结束后的状态图:
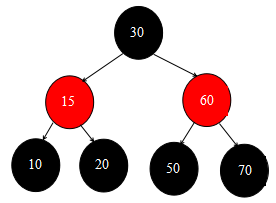
注:以上图片出处均为 博客园——五月的仓颉,非本人原创!
到这里,关于红黑树的所有知识全部都讲解完毕,并且集合的基础知识也暂告一段落了。
有的童鞋会问,怎么只讲了List、Map接口下的一些常用工具类,Set接口的怎么不讲了呢?
大家可以去看下HashSet、TreeSet的源码相关实现,其实就是HashSet、TreeSet去掉了Value而已,绝大多数实现都是一样的,所以我这里就不再去细说了
注意我在这个集合分类中所讲的集合类都是非线程安全的,像CopyOnWriteArrayList、ConcurrentHashMap、BlockingQueue等线程安全的集合工具类我会放在多线程的分类主题中去讲解。
OK,接下来我会更新一些多线程相关的知识,下期见!
