[学习笔记]树状数组

树状数组

要是别人说怀有希望是错误的事，无论多少次我都一定会反驳这句话。

• 基本代码

int lowbit(int t)
{
return t&(-t);
}
void add(int x,int y)
{
for(int i=x; i<=n; i+=lowbit(i))
tree[i]+=y;
}
int getsum(int x)
{
int ans=0;
for(int i=x;i>0;i-=lowbit(i))
ans+=tree[i];
return ans;
}

树状数组的作用：维护一个数组，重点不在这个数组，主要是是区间和的问题，它的查询和修改的时间复杂度都是log(n)，空间复杂度则为O(n)，这是因为树状数组通过将线性结构转化成树状结构，从而进行跳跃式扫描。通常使用在高效的计算数列的前缀和，区间和。

树状数组又叫二叉索引树，顾名思义肯定与二叉树有关。

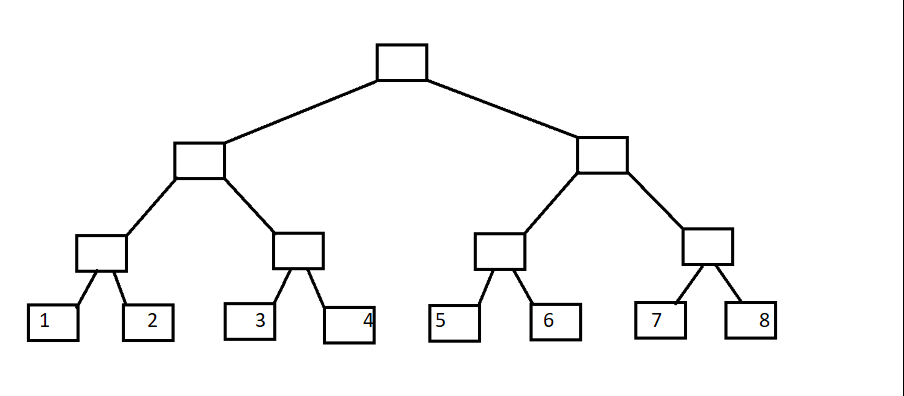
这是二叉树，然后变形一下：

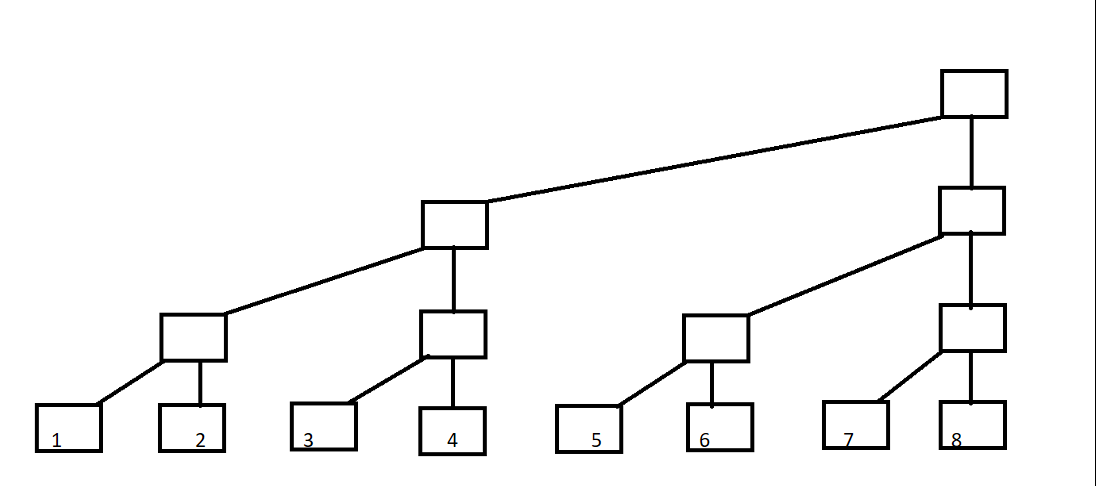
现在定义每一列的顶端结点C[]数组，以求和为例：

C[i]代表 子树的叶子结点的权值之和（不只是区间和）

C[1]=A[1];
C[2]=A[1]+A[2];
C[3]=A[3];
C[4]=A[1]+A[2]+A[3]+A[4];
C[5]=A[5];
C[6]=A[5]+A[6];
C[7]=A[7];
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

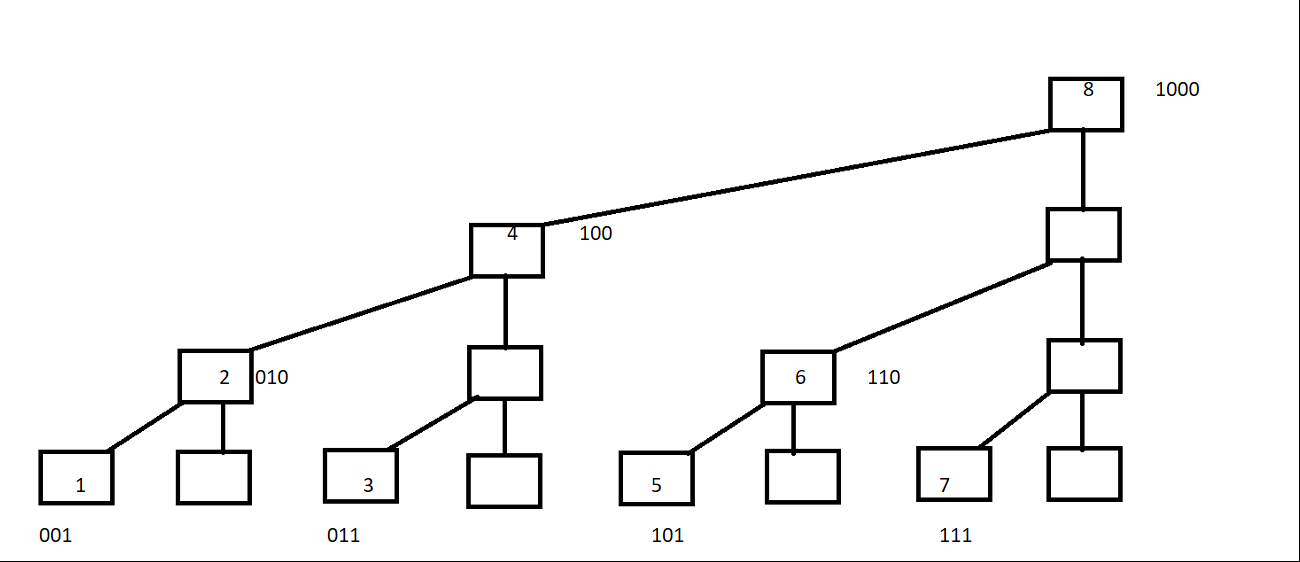
• 将C[ ]数组的结点序号转化为二进制

1=(001)      C[1]=A[1];
2=(010)      C[2]=A[1]+A[2];
3=(011)      C[3]=A[3];
4=(100)      C[4]=A[1]+A[2]+A[3]+A[4];
5=(101)      C[5]=A[5];
6=(110)      C[6]=A[5]+A[6];
7=(111)      C[7]=A[7];
8=(1000)    C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

对照式子可以发现
C[i]=A[i-2^k+1] + A[i-2^k+2]+......A[i]; （k为i的二进制中从最低位到高位连续零的长度）例如i=8时，有三个连续的0，所以k=3;
现在可以解释一下lowbit

lowbit

int lowbit(int t)
{
return t&(-t);
}
-t 代表t的负数 计算机中负数使用对应的正数的补码来表示
例如 :
 t=6（0110） 此时 k=1
-t=-6=(1001+1)=(1010)
 t&(-t)=(0010)=2=2^1
 而lowbit就是2^k

C[i]=A[i-2^k+1] + A[i-2^k+2]+......A[i];

C[i]=A[i-lowbit(i)+1]+A[i-lowbit(i)+2]+......A[i];

getsum

int getsum(int x)
{
int ans=0;
for(int i=x;i>0;i-=lowbit(i)) ans+=tree[i];
return ans;
}//区间查询 树状数组追其根本就是二进制的应用

下面利用C[i]数组，求A数组中前i项的和 
举个例子 i=7;
sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7] ;  
前i项和C[4]=A[1]+A[2]+A[3]+A[4];   
C[6]=A[5]+A[6];   C[7]=A[7];
可以推出:   sum[7]=C[4]+C[6]+C[7];
序号写为二进制: sum[(111)]=C[(100)]+C[(110)]+C[(111)];

再举个例子 i=5
sum[5]=A[1]+A[2]+A[3]+A[4]+A[5] ;   
前i项和C[4]=A[1]+A[2]+A[3]+A[4];   C[5]=A[5];
可以推出:   sum[5]=C[4]+C[5];
序号写为二进制: sum[(101)]=C[(100)]+C[(101)];

看不懂的话就结合代码演示一下：
i=7：ans=0；i-=1=>ans+=C[7];
i=6; ans=C[7];i-=2=>ans+=C[6];
i=4; ans=C[7]+C[4];i-=4=>ans+=C[4]
sum[7]=C[4]+C[6]+C[7]=ans;

add

void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i))
tree[i]+=y;
}

当更新A[1]时 需要向上更新C[1] ,C[2],C[4],C[8]
C[1], C[2], C[4], C[8]
写为二进制 C[(001)],C[(010)],C[(100)],C[(1000)]
1(001) C[1]+=A[1]
lowbit(1)=001 1+lowbit(1)=2(010) C[2]+=A[1]
lowbit(2)=010 2+lowbit(2)=4(100) C[4]+=A[1]
lowbit(4)=100 4+lowbit(4)=8(1000) C[8]+=A[1]

• 其实就是查找的逆过程。