在图形的显示过程中,因为屏幕显示的内容有限,所以需要裁剪
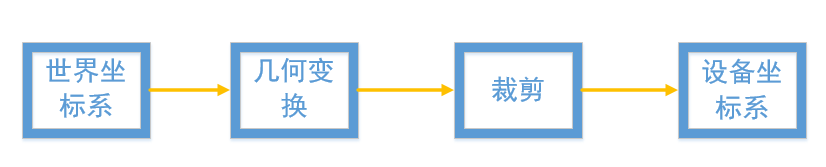
要实现这个转换,简便的方法是全部扫描一遍然后判断像素是不是落在视区中。
但是如果原图很大,这个遍历全部像素的方法效率较低。
最常用的是在世界坐标系上,对参数表示的图形裁剪。
裁剪的定义
判断图形元素是否落在裁剪窗口之内并找出其位于内部的部分
定义矩形裁剪窗口:(x_{min},y_{min}-x_{max},y_{max})
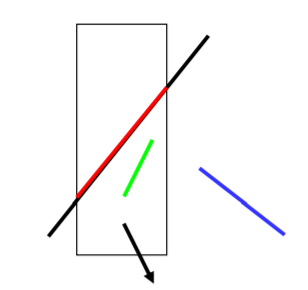
直线段的裁剪
定义直线段(P_0(x_0,y_0)P_1(x_1,x_2))
直线段与窗口的关系有:
- 完全可见:两个端点都位于窗口内
- 非显然不可见:线段至少有一端点位于窗口外
- 显然不可见:两个端点都位于窗口外?
两个端点位于窗口外不一定是显然不可见,也可能是非显然不可见。怎样才能算显然不可见?
为窗口边界画出延长线:
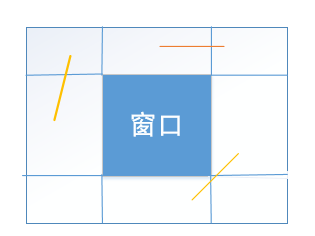
观察可以发现,如果两个端点位于同边界的外侧,就可以得出显然不可见的答案
右下角的线段应该属于非完全可见,非显然不可见,因为不属于同边界的外侧可能在屏幕中出现一部分。
这就要用到规范的编码算法
编码算法
设编码为(D_3D_2D_1D_0)
编码规则是:
当(x<x_{min}),(D_0=1),否则为(0)
当(x>x_{max}),(D_1=1),否则为(0)
当(y<y_{min}),(D_2=1),否则为(0)
当(y>y_{max}),(D_3=1),否则为(0)
得到一条直线,设端点的编码为code1和code2
- 若(code_1|code_2=0),线段在窗口内,完全可见
- 若(code1&code_2 eq0),线段在窗口外,非完全可见
其他情况:则为非完全可见,非显然不可见。
求线段与延长线的交点,其中一段肯定为显然不可见,对另外一段从第一步开始判断
观察:若两个code某一位上不同,说明线段与某个边相交,如(D_2)位不同,那就与下边相交。
适用范围
这个算法的好处是可以快速判断显然可见和显然不可见。
对于非显然不可见,最多需要求交点四次。
如从0101到1010,与边界可能交于4个点
对于窗口很大或者窗口很小的情况下效率较高
对于非矩形,凸多边形的情况下也可以使用编码算法,但随着边数增多,编码会变得复杂