Mayor's posters POJ

Mayor's posters

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 86160		Accepted: 24734

Description

The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules: 

• Every candidate can place exactly one poster on the wall. 
• All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown). 
• The wall is divided into segments and the width of each segment is one byte. 
• Each poster must completely cover a contiguous number of wall segments. 

They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections. 
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall. 

Input

The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l_i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l_i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l_i, l_i+1 ,... , ri. 

Output

For each input data set print the number of visible posters after all the posters are placed. 

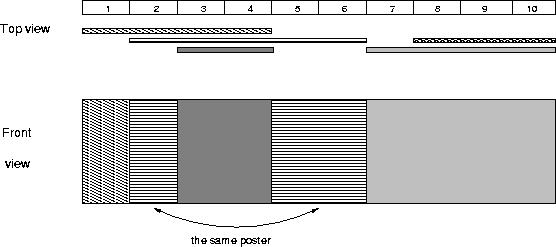
The picture below illustrates the case of the sample input. 

Sample Input

1
5
1 4
2 6
8 10
3 4
7 10

Sample Output

4

题意：画N条线段，顺序从先到后，后面画的线段可以覆盖之前画的线段，每种线段颜色不同，最后输出有多少墙上有多少种颜色。

题解：长度建线段树不可行，离散化后处理

离散化：只考虑元素之间的相互关系，比如 1 10000 10000000000，可以映射成1 2 3
离散化操作一般用STL的sort和unique:
数组a[n],b[n](a[n]的副本),先对数组b进行排序,再用unique去重,离散的时候用lower_bound

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<list>
#include<math.h>
#include<vector>
#include<stack>
#include<string>
#include<stdio.h>

using namespace std;
typedef long long LL;
const int MAXN = 2e4 + 10;
int st[MAXN << 2];
int vis[MAXN << 2];
int b[MAXN];
struct node {
    int a,b;
}a[MAXN];

void build(int o,int l,int r)
{
    st[o] = 0;
    if(l == r) return;
    int m = (l + r) >> 1;
    build(o << 1,l,m);
    build(o << 1 | 1,m + 1,r);
}
void pushdown(int o)
{
    if(st[o])
    {
        st[o << 1] = st[o];
        st[o << 1 | 1] = st[o];
        st[o] = 0;
    }
}
void update(int o,int l,int r,int ql,int qr,int val)
{
    if(ql <= l && r <= qr)
    {
        st[o] = val;
        return;
    }
    pushdown(o);
    int m = (l + r) >> 1;
    if(ql <= m) update(o << 1,l,m,ql,qr,val);
    if(qr > m) update(o << 1 | 1,m + 1,r,ql,qr,val);
}
int query(int o,int l,int r,int ind)
{
    if(l == r) return st[o];
    pushdown(o);
    int m = (l + r) >> 1;
    if(m >= ind) return query(o << 1 ,l,m,ind);
    else return query(o << 1 | 1,m + 1,r,ind);
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        memset(vis,0,sizeof vis);
        int n;
        scanf("%d",&n);
        build(1,1,2 * n);
        int cnt = 0;
        for(int i = 1; i <= n; i++)
        {
            scanf("%d %d",&a[i].a,&a[i].b);
            b[++cnt] = a[i].a;
            b[++cnt] = a[i].b;
        }
        sort(b + 1,b + 1 + cnt);
        cnt = unique(b + 1, b +1 + cnt) - b - 1;    //去重后的个数
        for(int i = 1; i <= n; i++)
        {
            int l = lower_bound(b + 1,b + 1 + cnt,a[i].a) - b;
            int r = lower_bound(b + 1,b + 1 + cnt,a[i].b) - b;
            update(1,1,2 * n,l,r,i);
        }
        for(int i = 1; i <= 2 * n; i++)
        {
            int tmp = query(1,1,2 * n,i);
//            printf("tmp = %d
",tmp);
            vis[tmp] = 1;
        }
        int sum = 0;
        for(int i = 1;i <= 2 * n; i++)
            sum += vis[i];
        printf("%d
",sum);
    }
}