[leetcode 周赛 160] 1238 循环码排列

1238 Circular Permutation in Binary Representation 循环码排列

问题描述

给你两个整数 n 和 start。你的任务是返回任意 (0,1,2,,...,2^n-1) 的排列 p，并且满足：

• p[0] = start
• p[i] 和 p[i+1] 的二进制表示形式只有一位不同
• p[0] 和 p[2^n -1] 的二进制表示形式也只有一位不同

示例 1：

输入： n = 2, start = 3
输出： [3,2,0,1]
解释： 这个排列的二进制表示是 (11,10,00,01)
所有的相邻元素都有一位是不同的，另一个有效的排列是 [3,1,0,2]

示例 2：

输出： n = 3, start = 2
输出： [2,6,7,5,4,0,1,3]
解释： 这个排列的二进制表示是 (010,110,111,101,100,000,001,011)

提示：

• 1 <= n <= 16
• 0 <= start < 2^n

思路

• 读题
  所求序列是一个格雷码序列, 相邻的二进制只有一位不同(有效位数), 首尾同样只有一位不同
  题目虽然给出了开始位置, 但其实就是一个循环, 找到一个循环序列即可

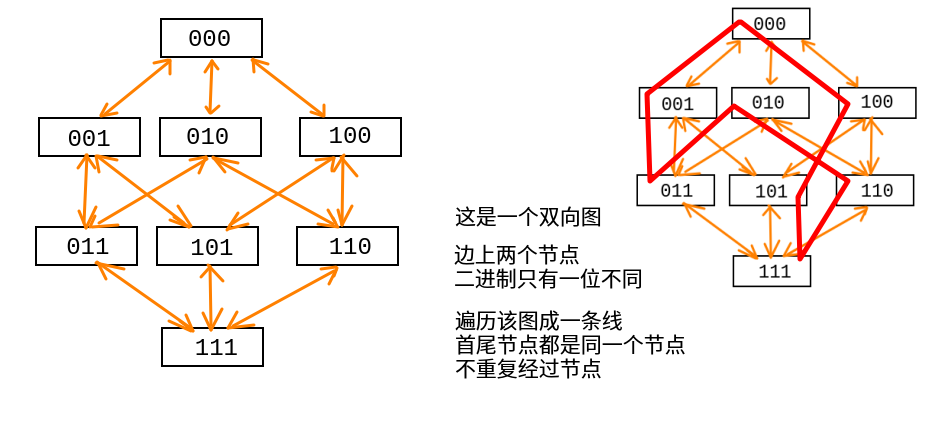
DFS图遍历

二进制, 从全0到全1, 每次改变一位, 生成一份边上两节点为只相差一位的图
从给定起始点出发, 选择一条边到下一节点, 不重复经过节点, 最终节点为自己
同以上方式, 筛选出一条循环的线路

格雷码生成

格雷码生成公式: [i] = i^(i>>>1) 自己与自己左移一位相异或

• 举例: 3位

i	i	i>>>1	[i]	[i]
0	000	000	000	0
1	001	000	001	1
2	010	001	011	3
3	011	001	010	2
4	100	010	110	6
5	101	010	111	7
6	110	011	101	5
7	111	011	100	4

代码实现

DFS图遍历

class Solution {
    public List<Integer> circularPermutation(int n, int start) {
        // 该序列节点数
        int len = 1 << n;
        // 在图遍历中 存储已经过的节点
        Set<Integer> visited = new HashSet<>(len);
        // 符合条件的答案 序列
        List<Integer> ans = new ArrayList<>(len);

        // 首先置入起点
        visited.add(start);
        ans.add(start);
        // 图遍历DFS开始
        dfs(n, start, ans, visited);

        return ans;
    }

    private boolean dfs(int n, int prev, List<Integer> ans, Set<Integer> visited) {
        // 判断是否进行到最后一个节点的判断
        if (ans.size() == (1 << n)) {
            // 判断首尾节点是否符合条件
            int first = ans.get(0), end = ans.get(ans.size() - 1);
            // 判断两数字是否只有一位不同: ((a^b)&((a^b)-1)) == 0
            // 解释: 如果两个数字只有一位不同, 那么相异或时相同位置为0 不同为置为1 即只有一位为1其余全为0
            int temp = first ^ end;
            // 如果First End只有一位不同 (101^001 --> 001 --> 001&000 == 0
            return (temp & (temp - 1)) == 0;
        }

        for (int i = 0; i < n; i++) {
            // 下一个符合条件的节点
            int next = prev ^ (1 << i);
            // 如果不曾访问过
            if (!visited.contains(next)) {
                visited.add(next);
                ans.add(next);
                // 寻找下一符合条件的节点
                if (dfs(n, next, ans, visited)) {
                    return true;
                }
                ans.remove(ans.size() - 1);
                visited.remove(next);
            }
        }

        return false;
    }
}

格雷码生成

class Solution {
    public List<Integer> circularPermutation(int n, int start) {
        int size = 1 << n;
        int[] arr = new int[size];
        // 生成格雷码
        for (int i = 0; i < size; i++) {
            arr[i] = i ^ (i>>>1);
        }

        List<Integer> ans = new ArrayList<>();
        for (int i = 0; i < size; i++) {
            // 从指定起始点开始
            if (arr[i] == start) {
                for (int j = 0; j < size; j++) {
                    int next = (i+j) % size;
                    ans.add(arr[next]);
                }
                return ans;
            }
        }

        return ans;
    }
}

参考资源

第 160 场周赛 全球排名