1229 Meeting Scheduler 安排会议日程
问题描述
你是一名行政助理, 手里有两位客户的空闲时间表: slots1 和 slots2, 以及会议的预计持续时间 duration, 请你为他们安排合适的会议时间.
「会议时间」是两位客户都有空参加, 并且持续时间能够满足预计时间 duration 的 最早的时间间隔.
如果没有满足要求的会议时间, 就请返回一个 空数组.
「空闲时间」的格式是 [start, end], 由开始时间 start 和结束时间 end 组成, 表示从 start 开始, 到 end 结束.
题目保证数据有效: 同一个人的空闲时间不会出现交叠的情况, 也就是说, 对于同一个人的两个空闲时间 [start1, end1] 和 [start2, end2], 要么 start1 > end2, 要么 start2 > end1.
**示例 1: **
**输入: ** slots1 = [[10,50],[60,120],[140,210]], slots2 = [[0,15],[60,70]], duration = 8
**输出: ** [60,68]
**示例 2: **
**输入: **slots1 = [[10,50],[60,120],[140,210]], slots2 = [[0,15],[60,70]], duration = 12
**输出: **[]
**提示: **
1 <= slots1.length, slots2.length <= 10^4slots1[i].length, slots2[i].length == 2slots1[i][0] < slots1[i][1]slots2[i][0] < slots2[i][1]0 <= slots1[i][j], slots2[i][j] <= 10^91 <= duration <= 10^6
思路
- 读题
- 同一客户的时间表不会交叉
- 会议时间在两用户空闲时间段交叉处, 即
min(end1, end2) - max(start1, start2) > 0 - 如果当前比较的两个时间段不符合, 则保留
end更大的时间段, 让对方下移
双指针遍历(排序)
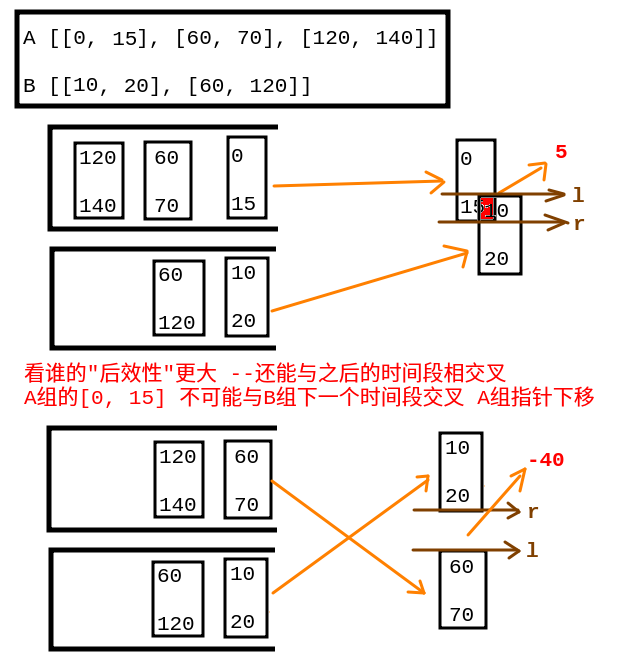
使用双指针分别指向两个用户的空闲时间表(排序), 两两比较min(end1, end2) - max(start1, start2) >= duration
如果当前比较的两个时间段不符合, 则保留
end更大的时间段, 让对方下移
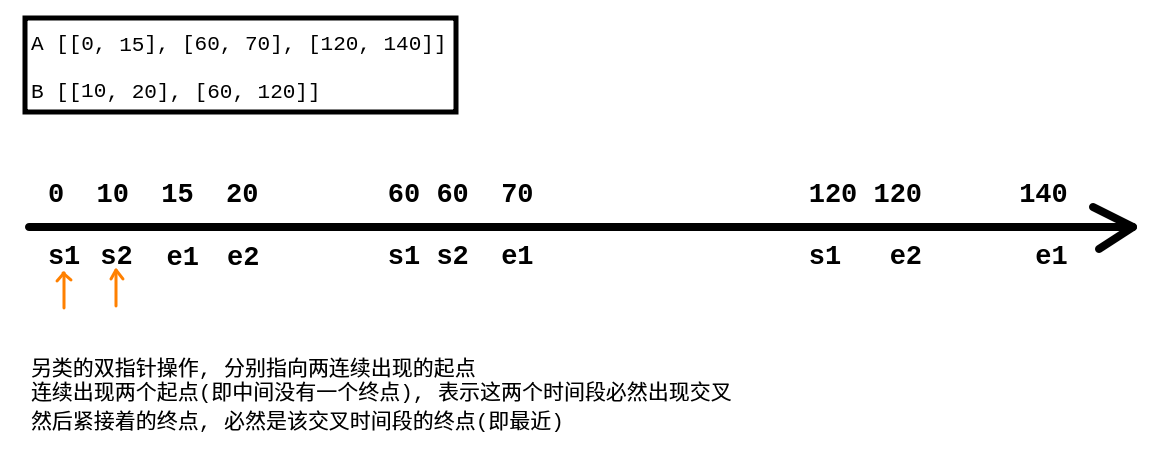
交叉时间段的规律
规律: 将所有时间段的起点和终点放置在x轴上, 并予以分别标注(slot1的起点为0, 终点为2/slot2的起点为1, 终点为4), 遍历这条轴, 如果连续遇到两个不同用户的起点, 则表示必定发生了交叉
代码实现
双指针遍历
class Solution {
public List<Integer> minAvailableDuration(int[][] slots1, int[][] slots2, int duration) {
// 对两个时间表 进行顺序排序
Arrays.sort(slots1, Comparator.comparingInt(s -> s[0]));
Arrays.sort(slots2, Comparator.comparingInt(s -> s[0]));
// c1 指针, 指向当前遍历slot1的位置
// c2 指针, 指向当前遍历slot1的位置
// l 当前遍历的两时间段 起点的最大值
// r 当前遍历的两时间段 终点的最小值
int c1 = 0, c2 = 0, len1 = slots1.length, len2 = slots2.length, l, r;
// s1 slot1当前遍历时间段
// s2 slot2当前遍历时间段
int[] s1, s2;
List<Integer> ans = new ArrayList<>();
while (c1 < len1 && c2 < len2) {
s1 = slots1[c1];
s2 = slots2[c2];
l = Math.max(s1[0], s2[0]);
r = Math.min(s1[1], s2[1]);
// 两个时间段的交集符合条件 (r-l)>=duration
System.out.printf("[r:%d, l:%d]:(%d) <-- s1:[%d, %d], s2:[%d, %d]
",
r, l, (r - l), s1[0], s1[1], s2[0], s2[1]);
if (r - l >= duration) {
ans.add(l);
ans.add(l + duration);
break;
} else if (s1[1] == r) {
// 此时 slot1的终点比slot2的小 slot2更有机会 有slot1其后的时间段交叉
// slot1需要移动到下一个时间段
c1++;
} else {
c2++;
}
}
return ans;
}
}
- 可以不使用Arrays提供的工具方法, 手写一个伴随1维数组排序的2维数组
/**
* 使用堆排进行二维数组排序
*
* @param arrs 被排序二维数组
*/
public static void sort2DArray(int[][] arrs) {
if (Objects.isNull(arrs)) {
System.out.println("arrs is not a array");
return;
}
int len = arrs.length, d = arrs[0].length, needD = 2;
if (d != needD) {
System.out.printf("arrs is not a 2d array [d:%d]
", d);
return;
}
int end = len - 1, root = 0, d1 = 0, d2 = 1;
while (end >= root) {
for (int child = end; child > root; child--) {
int parent = (child - 1) >>> 1;
if (arrs[child][d1] > arrs[parent][d1]) {
swap(child, parent, arrs, d1);
swap(child, parent, arrs, d2);
} else if (arrs[child][d1] == arrs[parent][d1] && arrs[child][d2] > arrs[parent][d2]) {
swap(child, parent, arrs, d2);
}
}
swap(end, root, arrs, d1);
swap(end, root, arrs, d2);
end--;
}
}
private static void swap(int c, int p, int[][] arrs, int d) {
int temp = arrs[c][d];
arrs[c][d] = arrs[p][d];
arrs[p][d] = temp;
}
交叉时间段的规律
- 使用自定义Pair类 作为排序的基本单位 使得终点伴随起点排序
class Solution {
/**
* 一种统一的标示
*/
private static int s1Start = 0, s2Start = 1, s1End = 2, s2End = 3;
/**
* pair<时间点, 标识>对
* 可以排序时间点的同时, 以此改变标识的位置
*/
class Pair {
/**
* 存储的时间点
*/
int element;
/**
* 时间间断开始 0 1
* 时间间断结束 2 3
*/
int flag;
Pair(int element, int flag) {
this.element = element;
this.flag = flag;
}
@Override
public boolean equals(Object o) {
if (this == o) {
return true;
}
if (o == null || getClass() != o.getClass()) {
return false;
}
Pair pair = (Pair) o;
return element == pair.element &&
flag == pair.flag;
}
@Override
public int hashCode() {
return Objects.hash(element, flag);
}
@Override
public String toString() {
return "Pair{" +
"element=" + element +
", flag=" + flag +
'}';
}
}
public List<Integer> minAvailableDuration(int[][] slots1, int[][] slots2, int duration) {
// 存储pair对 注意Comparator不能只写element 添加数据时 会以此作为元素是否重复的判断依据!
// TreeSet 带排序的Set容器
Set<Pair> pairs = new TreeSet<>((o1, o2) -> {
// 在时间点相同的情况下 根据 起点>终点 的顺序排序
if (o1.element == o2.element) {
return o1.flag - o2.flag;
}
return o1.element - o2.element;
});
// 初始化
for (int[] s1 : slots1) {
pairs.add(new Pair(s1[0], s1Start));
pairs.add(new Pair(s1[1], s1End));
}
for (int[] s2 : slots2) {
pairs.add(new Pair(s2[0], s2Start));
pairs.add(new Pair(s2[1], s2End));
}
// ans 最终返回结果
List<Integer> ans = new ArrayList<>();
// s1 遍历到slot1最近的起点 即当前遍历位置的最近slot1起点
// s2 遍历到slot2最近的起点
// cnt 以及遍历到的起点 为2时 如果接下来是终点 则表示必定有交集!
int s1 = 0, s2 = 0, cnt = 0;
for (Pair pair : pairs) {
System.out.printf("%s [s1:%d s2:%d] cnt:%d
", pair, s1, s2, cnt);
if (pair.flag == s1Start) {
s1 = pair.element;
cnt++;
} else if (pair.flag == s2Start) {
s2 = pair.element;
cnt++;
} else if (pair.flag == s1End || pair.flag == s2End) {
// 连续两个起点, 必定有一交集
if (cnt == 2) {
// near 离当前遍历终点最近的起点(越大越近)
int near = Math.max(s1, s2), e = pair.element;
System.out.printf("%s [s1:%d s2:%d] near:%d
", pair, s1, s2, near);
if (near + duration <= e) {
ans.add(near);
ans.add(near + duration);
break;
}
}
// 这个终点不符合 相当于有一起点无用 还需要继续找下一交集
cnt--;
}
}
return ans;
}
}