1151 Minimum Swaps to Group All 1's Together 最少交换次数来组合所有的 1
描述
给出一个二进制数组data,你需要通过交换位置,将数组中任何位置上的1组合到一起,并返回所有可能中所需最少的交换次数。
- 示例 1:
输入:[1,0,1,0,1]
输出:1
解释:
有三种可能的方法可以把所有的 1 组合在一起:
[1,1,1,0,0],交换 1 次;
[0,1,1,1,0],交换 2 次;
[0,0,1,1,1],交换 1 次。
所以最少的交换次数为 1。
- 示例 2:
输入:[0,0,0,1,0]
输出:0
解释:
由于数组中只有一个 1,所以不需要交换。
- 示例 3:
输入:[1,0,1,0,1,0,0,1,1,0,1]
输出:3
解释:
交换 3 次,一种可行的只用 3 次交换的解决方案是 [0,0,0,0,0,1,1,1,1,1,1]。
- 提示:
1 <= data.length <= 10^5
0 <= data[i] <= 1
思路
- 已知条件
- 二进制数组 只有0/1
- 交换的方式 双方任意交换
- 题目要求
将数组中任何位置上的1组合到一起, 使用最少的交换次数
因为交换方式是任意的, 所以可以指定一段空间(大小为数组中1的个数)给它, 将其他1交换过来
此时因为1和1没有必要交换, 只交换1和0, 所以该段空间中0的个数就是交换次数
又因为空间是固定的, 0和1个数是可以相互转换, 即空间大小-该空间所有1相加=0的个数=交换次数
每段空间中最多的1 --> 每段空间中和最大 --> 每段空间0的个数最少 --> 交换次数最少
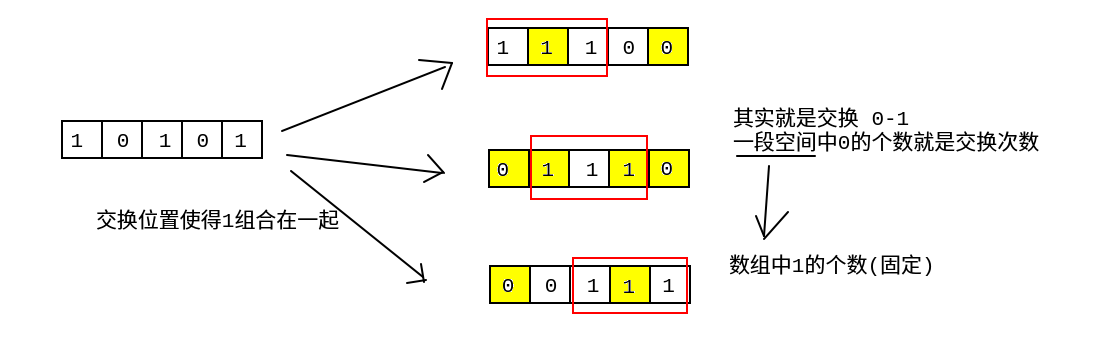
对于求取每一段空间大小和该空间所有1的和
遍历会超出时间限制
因此采用动规记录表的方法
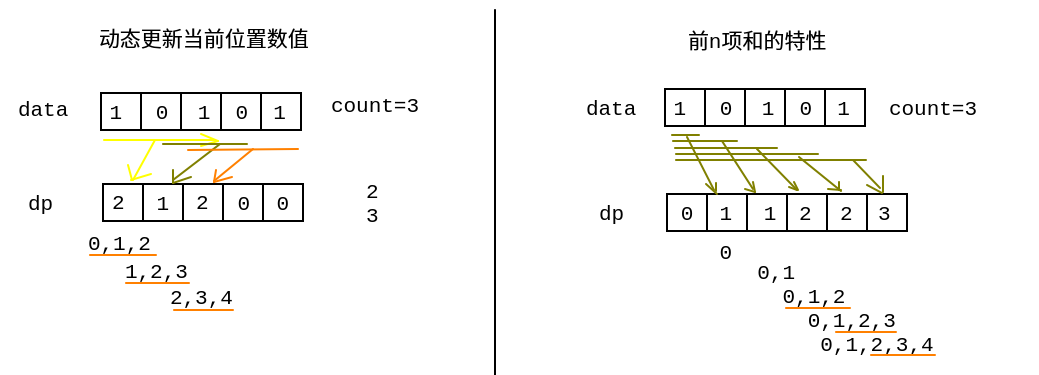
代码实现
动规求取每count区域的和(动态更新当前位置数值)
class Solution {
public int minSwaps(int[] data) {
int len = data.length;
// 个数只有1/2的数组 0 1 01 10 11 00 必定返回0
if (len == 1 | len == 2) return 0;
// count data数组中1的个数
int count = 0;
// 因为是个二进制数组 该数组的和就是1的个数
for (int i : data) count += i;
// 数组中只有1个1 或没有1
if (count == 1 | count == 0) return 0;
// 数组中全是1
if (count == len) return 0;
// dp 表示 i ~ i+count 该段空间中1的个数
int[] dp = new int[len];
// dp[0]
for (int i = 0; i < count; i++) {
dp[0] += data[i];
}
// cur 表示当前控制空间1的个数
// maxSum 表示该数组每段空间1的最多个数
int cur = 0, maxSum = dp[0];
for (int i = 1; i < len - count + 1; i++) {
// 动态更新当前位置数值
// 每次移动删除最前的数值 加上最新的数值 --这让我想起了队列
cur = dp[i-1] - data[i-1] + data[i+count-1];
dp[i] = cur;
maxSum = (maxSum > cur) ? maxSum : cur;
}
// 反推0的个数 即最小交换次数
return count-maxSum;
}
}
动规求取每count区域的和(前n项和的特性:前n和-前n-k和=[n-k, n]的和)
class Solution {
public int minSwaps(int[] data) {
int len = data.length;
if (len <= 2) return 0;
// dp 表示数组 (0, i] 的和
int[] dp = new int[len+1];
dp[0] = 0;
for (int i = 0; i < len; i++) {
dp[i+1] = dp[i] + data[i];
}
// count 数组中1的个数
int count = dp[len];
if (count == 1 | count == 0) return 0;
if (count == len) return 0;
// cur 表示当前控制空间1的个数
// maxSum 表示该数组每段空间1的最多个数
int cur = 0, maxSum = 0;
for (int i = 0; i + count <= len; i++) {
// 前n和-前n-k和=[n-k, n]的和
cur = dp[i+count] - dp[i];
maxSum = maxSum >= cur ? maxSum : cur;
}
return count-maxSum;
}
}
使用队列的解法 队列只是用来控制顺序(边界问题) 实际意义并不大
class Solution {
public int minSwaps(int[] data) {
int len = data.length;
if (len <= 2) return 0;
// count 数组中1的个数
int count = 0;
for (int i : data) count += i;
if (count <= 1 | count >= len) return 0;
// q 队列 用于控制顺序 保证先进先出 删除头一个 插入尾一个
Queue<Integer> q = new LinkedList<>();
// maxSum 表示该数组每段空间1的最多个数
int maxSum = 0;
// 初始化 第一轮
for (int i = 0; i < count; i++) {
q.add(data[i]);
maxSum += data[i];
}
// pre 头一个被删除的数据(出队列)
// curSum 当前队列中数据和
int pre = 0, curSum = maxSum;
// 头元素出队列 data当前数据入队列 当前和更新
for (int i = count; i < len; i++) {
pre = q.poll();
q.add(data[i]);
curSum = curSum - pre + data[i];
maxSum = maxSum >= curSum ? maxSum : curSum;
}
return count-maxSum;
}
}