题目:二维数组中的查找
描述
在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。
请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
思路
根据二维数组递增的特性,查找的形式如下:
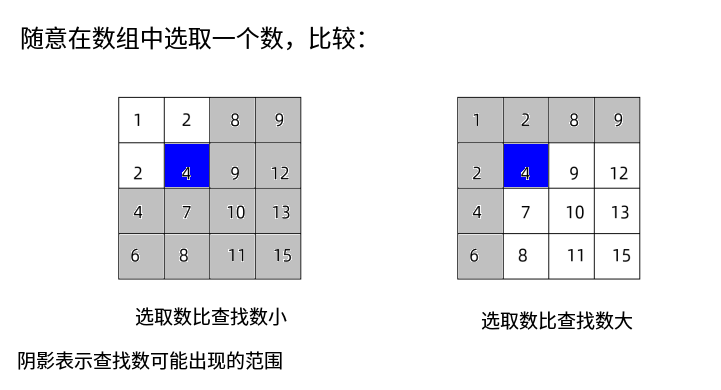
-
暴力破解可以解决问题
按行遍历,直到等于查找数/大于查找数/越界 -
可以从边界出发
利用特性,可以确定一整列或整行的是否在查找范围
比如:从右上角出发,第一个数字表示该列的最小值,该行最大值
如果查找数比该列最小值还小,则表示该列不在查找范围
如果查找数比该行最大值还大,则表示该行不在查找范围

类似递归方法,每次都在缩减数据规模,将问题转化为更小的同样性质的问题

算法实现
class Solution {
/************
* 暴力遍历
* 每一行遍历 直到等于查找数/大于查找数/越界
*/
public boolean bruteFind(int[][] matrix, int target) {
if (matrix == null) return false;
int row = matrix.length, col = matrix[0].length;
int i = 0, j = 0;
// 遍历每一行
for (; i < row; i++) {
for (j = 0; j < col; j++) {
// 等于查找数
if (matrix[i][j] == target) {
return true;
} else if (matrix[i][j] > target) {
// 大于查找数
break;
}
}
}
return false;
}
/**************
* 沿着边缘开始查找
*
* 每一次都正确的排除干扰项
* 类似递归方法,每次都在缩减数据规模,将问题转化为更小的同样性质的问题
*/
public boolean edgeFirstFind(int[][] matrix, int target) {
if (matrix == null) return false;
int row = matrix.length, col = matrix[0].length;
int i = 0, j = col-1;
while (i < row && j >= 0) {
// 小于每一列的最小值
if (matrix[i][j] > target) {
j--;
} else if (matrix[i][j] < target) {
// 大于每一行的最大值
i++;
} else {
return true;
}
}
return false;
}
}
- 测试
/**
* FindFromArray2D
*
* 从二维数组中查找数字
* 二维数组格式:
* 从左到右 递增
* 从上到下 递增
*/
public class FindFromArray2D {
static Solution s = new Solution();
public static void main(String[] args) {
int[][] matrix = {
{1,2,8,9},
{2,4,9,12},
{4,7,10,13},
{6,8,11,15}
};
// 四个角
// 最小值
unitTest(matrix, 1);
unitTest(matrix, 9);
unitTest(matrix, 6);
// 最大值
unitTest(matrix, 15);
// 中心位置
unitTest(matrix, 10);
unitTest(matrix, 7);
// 错误数字
// 小于最小值
unitTest(matrix, 0);
// 介于最大、最小之间
unitTest(matrix, 5);
// 大于最大值
unitTest(matrix, 20);
}
private static void unitTest(int[][] matrix, int target) {
System.out.println("By Brute: " + s.bruteFind(matrix, target));
System.out.println("By Edge : " + s.edgeFirstFind(matrix, target));
}
}