题目:935. Knight Dialer 骑士拨号器
问题描述
国际象棋中的骑士可以按下图所示进行移动:

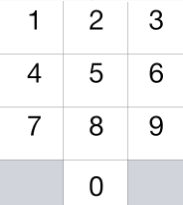
这一次,我们将 “骑士” 放在电话拨号盘的任意数字键(如上图所示)上,接下来,骑士将会跳 N-1 步。每一步必须是从一个数字键跳到另一个数字键。
每当它落在一个键上(包括骑士的初始位置),都会拨出键所对应的数字,总共按下 N 位数字。
你能用这种方式拨出多少个不同的号码?
因为答案可能很大,所以输出答案模 10^9 + 7。
- 示例 1:
输入:1
输出:10
- 示例 2:
输入:2
输出:20
- 示例 3:
输入:3
输出:46
- 提示:
1 <= N <= 5000
思路1
首先,我们来看下骑士在拨号盘上的走位
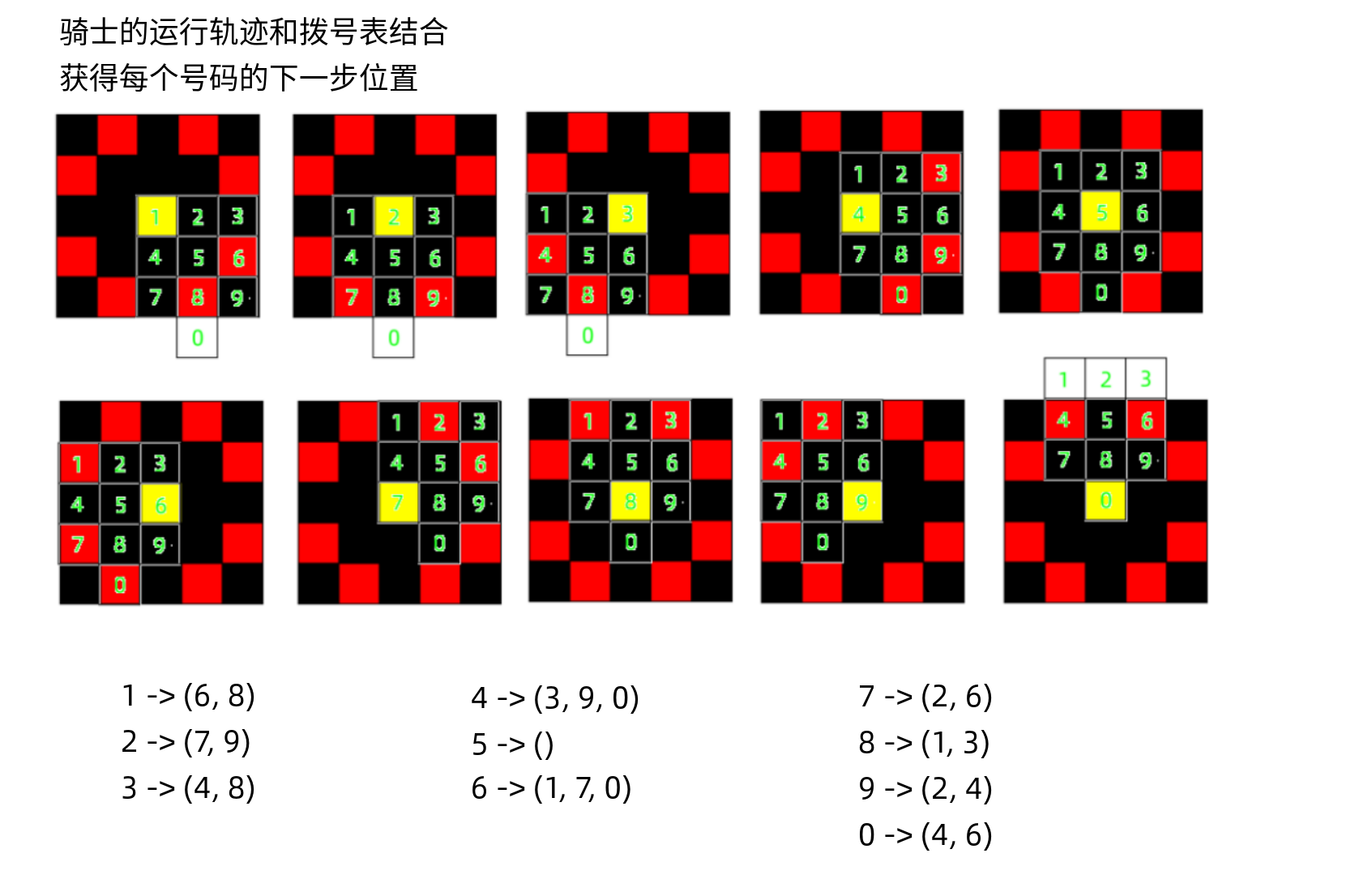
利用动态规划的思路,每一轮的结果都是由上一轮运算得到的(第一轮除外)
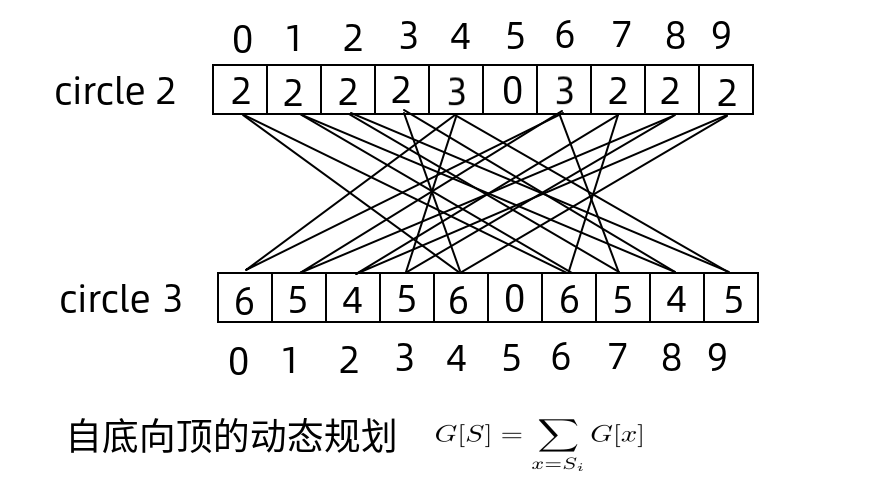
算法实现
- 无法通过OJ
- 思路是正确的,限于数据类型,求取更大的数值会溢出
class Solution {
public int knightDialer(int N) {
if (N == 1) return 10;
// 第二轮 每个键位下一步数
int[] jumpSizes = {2,2,2,2,3,0,3,2,2,2};
// 临时存放 运算的值
int[] tempSizes = new int[10];
// 从底层开始 推理出顶层的答案
for (int i = 2; i < N; i++) {
giveNum(tempSizes,0, jumpSizes, 4, 6);
giveNum(tempSizes,1, jumpSizes, 6, 8);
giveNum(tempSizes,2, jumpSizes, 7, 9);
giveNum(tempSizes,3, jumpSizes, 4, 8);
giveNum(tempSizes,4, jumpSizes, 3, 9, 0);
giveNum(tempSizes,6, jumpSizes, 1, 7, 0);
giveNum(tempSizes,7, jumpSizes, 2, 6);
giveNum(tempSizes,8, jumpSizes, 1, 3);
giveNum(tempSizes,9, jumpSizes, 2, 4);
tempSizes[5] = 0;
// 更新当前轮次的结果
jumpSizes = Arrays.copyOf(tempSizes, 10);
}
int sum = 0;
for (int num : jumpSizes) sum += num;
return sum;
}
void giveNum(int[] dest, int i, int[] src, int j, int k) {
dest[i] = src[j] + src[k];
}
void giveNum(int[] dest, int i, int[] src, int j, int k, int p) {
dest[i] = src[j] + src[k] + src[p];
}
}
- 可以通过OJ
- 过程一样,只是改变数据类型,加上取模
class Solution {
int mod = 1000000007;
public int knightDialer(int N) {
if (N == 1) return 10;
// 将int改为long 数据不会溢出
long[] jumpSizes = {2,2,2,2,3,0,3,2,2,2};
long[] tempSizes = new long[10];
long sum = 0;
for (int i = 2; i < N; i++) {
giveNum(tempSizes,0, jumpSizes, 4, 6);
giveNum(tempSizes,1, jumpSizes, 6, 8);
giveNum(tempSizes,2, jumpSizes, 7, 9);
giveNum(tempSizes,3, jumpSizes, 4, 8);
giveNum(tempSizes,4, jumpSizes, 3, 9, 0);
giveNum(tempSizes,6, jumpSizes, 1, 7, 0);
giveNum(tempSizes,7, jumpSizes, 2, 6);
giveNum(tempSizes,8, jumpSizes, 1, 3);
giveNum(tempSizes,9, jumpSizes, 2, 4);
tempSizes[5] = 0;
jumpSizes = Arrays.copyOf(tempSizes, 10);
}
for (long num : jumpSizes) sum += num;
return (int)(sum%mod);
}
void giveNum(long[] dest, int i, long[] src, int j, int k) {
// 每次求和后 都进行取模
dest[i] = (src[j] + src[k]) % mod;
}
void giveNum(long[] dest, int i, long[] src, int j, int k, int p) {
dest[i] = (src[j] + src[k] + src[p]) % mod;
}
}
思路2
通过观察各键位的位置以及其运算轨迹,总结出规律
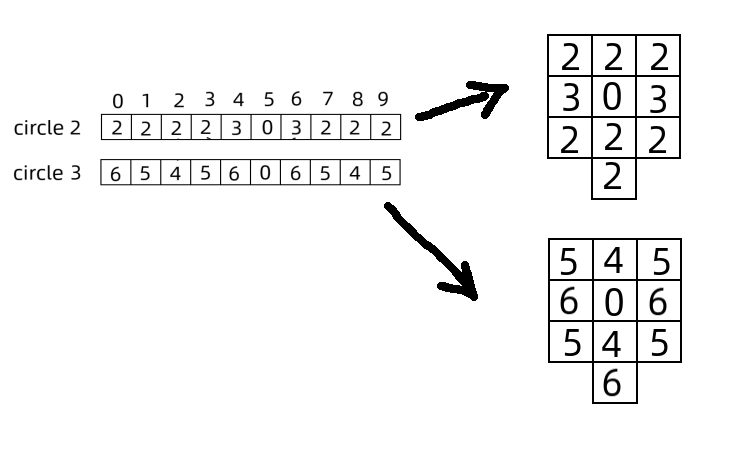



算法实现
class Solution {
public int knightDialer(int N) {
if (N == 1) return 10;
int mod = 1000000007;
// a表示四角的和
// b表示中部左右的和
// c表示中部上下的和
// d表示0键位的值
long a = 4, b = 2, c = 2, d = 1;
for (int i = 1; i < N; i++) {
long A = (2*(b+c)) % mod;
long B = (a + 2*d) % mod;
c = a;
d = b;
a = A;
b = B;
}
return (int)((a+b+c+d)%mod);
}
}