一、项目地址
https://github.com/Slontia/Sudoku
附加作业(GUI):https://github.com/Slontia/SudokuGUI
二、开发时间
|
PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
|
|
|
· Estimate |
· 估计这个任务需要多少时间 |
5 |
|
|
Development |
开发 |
|
|
|
· Analysis |
· 需求分析 (包括学习新技术) |
10 |
|
|
· Design Spec |
· 生成设计文档 |
0 |
|
|
· Design Review |
· 设计复审 (和同事审核设计文档) |
0 |
|
|
· Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
0 |
|
|
· Design |
· 具体设计 |
20 |
|
|
· Coding |
· 具体编码 |
720 |
|
|
· Code Review |
· 代码复审 |
20 |
|
|
· Test |
· 测试(自我测试,修改代码,提交修改) |
200 |
|
|
Reporting |
报告 |
|
|
|
· Test Report |
· 测试报告 |
60 |
|
|
· Size Measurement |
· 计算工作量 |
10 |
|
|
· Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
30 |
|
|
|
合计 |
1075 |
|
三、解题思路描述
刚开始看到这个题目的时候,我把-c和-s看成了相互独立的两个部分,用不同的思路分别解决。
关于数独的生成(create)
在数独游戏中,数字仅仅是作为一个符号,并无实际的意义区别。因此对于同一个数独,如果将上面的数字进行交换,就可以生成一个新的数独。如下图,由于我的学号是3,因此要将数字三固定在(R1, C1)的位置,而余下的a~h的位置可以放入不同的数字,这样就可以由一个数独引发出8!≈40000个新的数独。为此,我们只要准备25个数独模板,就可以保证生成1’000’000个互不相同的数独。
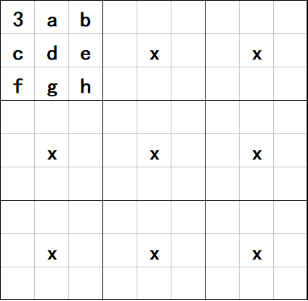
图1 数独生成示意
模板的生成,我决定采用3-3-3位置轮换的方法生成一个数独终盘,思路如下图所示,其中a~i分别代表一种数字:
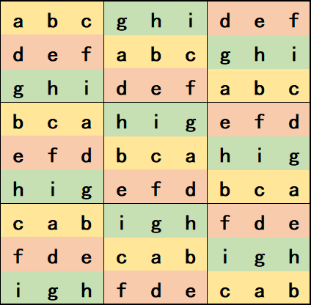
图2 数独模板
这样子只需要变动“abc”、“def”、“ghi”的排列,就可以得到一个符合规则的数独终盘。
在此基础上,通过改变R4~R6这三行的上下排列顺序,共可产生3!=6种组合,R7~R9同理。由于R4~R6的变换和R7~R9的变换相互独立,共可产生6*6=36中组合,我们需要的模板数是25个,36种组合已经达到了我们的要求。
关于数独的解决(solve)
一看到这道题,我的第一反应是采用“回溯法”,让计算机不断地尝试填入数字直到试出最终解。但是回溯需要占用很多的空间和时间,暴力回溯并不是合理的做法,于是我开始思考怎样才能缩小计算机尝试填入数字的范围。
这时候,我们定义一个概念“组”。在数独中,行、列、宫具备相同的性质,即包含且仅包含互不重复的1~9九个数字,于是我们将具有这种性质的集合统称为“组”。这样的话,行、列、宫本质上就可以看做为“组”。
最容易想到的是,根据规则,同一个组中不能出现相同的数字,所以当计算机尝试填入一个值的时候,只要是同组中有的数字,都没有尝试的必要,因此必须通过某种手段记录行、列、宫中已经有的数字。于是,我想到了计算机最擅长处理的“位运算”。
我的想法是,每个方格和每个组分别有一个二进制数,对于方格而言,二进制数的意义是记录所有可能的取值;对于组而言,二进制数的意义是记录组内已经确定的数字。这样进行方格取值可能性的更新时会很方便,只要对组二进制数取反,再和方格二进制数做“与”运算,很快就能缩小取值的范围。
比如,组二进制数值为0b0000_1001,表示该组已经有了1和4;方格二进制值数为0b0001_0101,表示该方格的可能取值为1、3和5。假如该方格为该组成员,则将前者取反与后者进行与运算,得到结果0b0001_0100,表示排除了取值为1的可能性,只剩下3和5。
除此之外,对方格进行值的猜测时,要优先选择那些可能性较少的数,这样可以尽可能快地多确定数字,排除余下方格的部分可能取值。
值得注意的是,一开始我认为一个数字的可能取值只剩下一个就代表这个数字被确定了,直到测试的时候才发现,有的数独是没有解的。因此判断一个方格的取值时,要对每一种可能性一一验证,不能通过“排除”的方式确定取值。
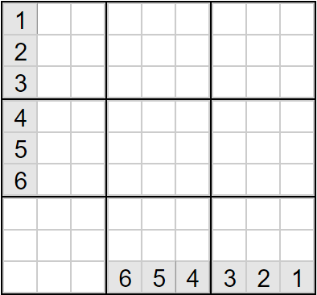
图3 一个很简单的无解数独
四、设计实现过程
关于数独的生成(create)
这里我设计了两个类:模板类和模板数独类,前者负责轮换所有的模板(36个),后者负责轮换填入的数字,并将结果输出。
这里的设计思路比较简单,大致的流程如下:

图4 数独生成流程图
关于数独的解决(solve)
根据之前的思路,我设计了三个类:数独类(Subject_sudoku)、组类(Group)、方格类(Box)。
数独类包含三个组数组,名字分别为rows[9]、columns[9]和blocks[9],分别代表思路中描述的三种组。每个组包括指向9个Box的指针和记录以确定数字的二进制数hasvalue。
在初始化数组之后,首先找到未确定值得Box中可能取值最少的那个,依次对它的值进行猜测。在每次猜测之前,通过拷贝构造将Subject_sudoku备份下来,在新的数独中将该方格的值确定,再继续寻找可能取值最少的Box,对它的值进行猜测,直到所有的Box的值都被确定,或尝试完某个Box的所有可能性(无解)。
基本流程描述如下:
1.初始化数独;
2.找到可能取值最少的Box;
3.依次假定它所有的可能取值;
4.重复2、3,直到所有Box都被确定,或尝试完某Box所有可能性。
对象之间的关系构成网状结构,便于Box和Group之间的信息传递,如下图:
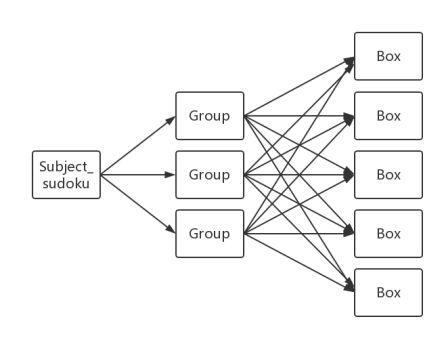
图5 类构成的三级网状结构
关于单元测试
对于-c功能的测试,主要测试以下三点:生成数量是否符合预期、生成数独是否符合规则、数独是否有重复。
第一点还好说,只要计个数和预期比对一下就行了;
第二点我还是采用位运算的方式,将每一个Box的值标记在所属Group的二进制数上,如果这个Group中的所有成员符合要求,即覆盖了1~9中的所有数字,则这个二进制数的值应当是0b1111_1111,即511;
第三点我采用字典树的方式检测重复,时间比两两比较要少的多。
五、测试
首先测试程序是否可以识别非法输入:
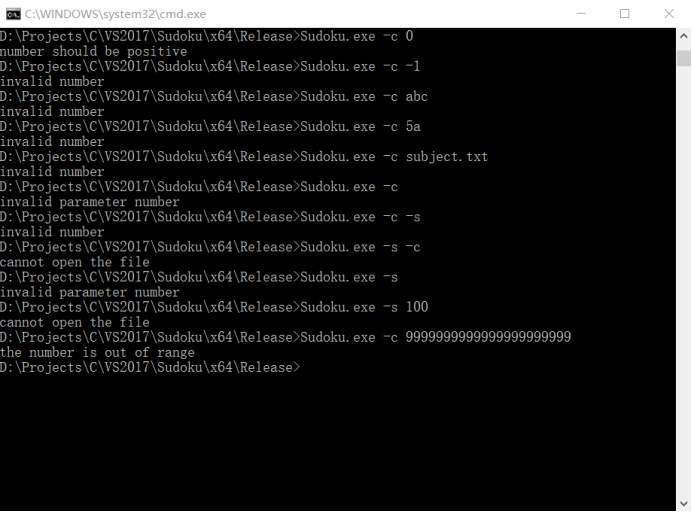
图6 非法输入样例
构造单元测试样例,test_c是对-c功能进行测试,c0~6目的是检测输出各种数量级数独的正确性,c_zero是测试前置0输入;test_s是对-s功能进行测试。

1 TEST_METHOD(c0) { 2 test_c("1", 1); 3 } 4 5 TEST_METHOD(c1) { 6 test_c("10", 10); 7 } 8 9 TEST_METHOD(c2) { 10 test_c("100", 100); 11 } 12 13 TEST_METHOD(c3) { 14 test_c("1000", 1000); 15 } 16 17 TEST_METHOD(c4) { 18 test_c("10000", 10000); 19 } 20 21 TEST_METHOD(c5) { 22 test_c("100000", 100000); 23 } 24 25 TEST_METHOD(c6) { 26 test_c("1000000", 1000000); 27 } 28 29 TEST_METHOD(c_zero) { 30 test_c("000005", 5); 31 } 32 33 TEST_METHOD(s1) { 34 test_s("subject.txt"); 35 }
test_文件内容如下:

// 简单测试 3 1 2 7 8 9 4 5 6 4 5 6 3 1 2 7 8 9 7 8 9 4 5 6 3 1 2 2 3 1 9 7 8 6 4 5 0 0 0 0 0 0 0 0 0 9 7 8 6 4 5 2 3 1 1 2 3 8 9 7 5 6 4 5 6 4 1 2 3 8 9 7 8 9 7 5 6 4 1 2 3 // 边界测试 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 // 一般测试 0 0 7 2 3 8 0 0 0 0 6 0 7 0 0 0 5 0 0 0 0 4 0 0 0 0 2 9 0 0 0 0 0 8 6 7 1 0 0 0 0 0 0 0 3 6 4 8 0 0 0 0 0 5 7 0 0 0 0 3 0 0 0 0 2 0 0 0 5 0 3 0 0 0 0 1 7 4 9 0 0 // 无解测试 1 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0 0 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 6 7 5 4 3 2 1 // 困难测试(据说是世界上最难的数独) 8 0 0 0 0 0 0 0 0 0 0 3 6 0 0 0 0 0 0 7 0 0 9 0 2 0 0 0 5 0 0 0 7 0 0 0 0 0 0 0 4 5 7 0 0 0 0 0 1 0 0 0 3 0 0 0 1 0 0 0 0 6 8 0 0 8 5 0 0 0 1 0 0 9 0 0 0 0 4 0 0 1 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0 0 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 0 6 0 0 0 0 0 0 0 0 0 7 0 0 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 0 0 9
由于单元测试无法检测覆盖率,所以我暂时修改了main函数……
1 int main() { 2 create_sudoku(1'000'000); 3 FILE* file = fopen("subject.txt", "r"); 4 if (file != NULL) { 5 solve_sudoku(file); 6 fclose(file); 7 } 8 return 0; 9 }
以上的测试样例已经在单元测试中通过,覆盖率结果显示已经覆盖了所有分支:
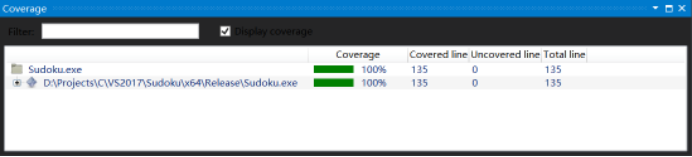
图7 覆盖了所有分支
六、性能分析与代码改进
参数设置为“-c 1000000”。以下是第一次分析的结果:
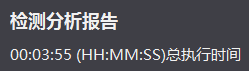
图8 第一次分析执行时间3分55秒

图9 第一次分析函数工作时间情况
可以看到,占用时间最长的是record函数和fputc函数,record函数的代码如下:
1 void Template_sudoku::record(FILE* fout) {
2 int counter;
3
4 for (int i = 0; i < 8; i += 3) { // each big line
5 for (int j = 0; j < 3; j++) { // each small line
6 counter = 0;
7 for (int k = 0; k < 3; k++) { // each block
8 for (char &c : templet->line[i + k][j]) {
9 fputc(code[c - '0'], fout);
10 fputc((counter++ < 8) ? ' ' : '
', fout);
11 }
12 }
13 }
14 }
15 }
经过将字符存储在字符串中一起输出的改进,第二次有了很大改变:

图10 第二次分析执行时间10.9秒

图11 第二次分析函数工作时间情况
改进后的代码如下:
1 void Template_sudoku::record(FILE* fout) {
2 int counter;
3 char output[300];
4 int index = 0;
5
6 for (int i = 0; i < 8; i += 3) { // each big line
7 for (int j = 0; j < 3; j++) { // each small line
8 counter = 0;
9 for (int k = 0; k < 3; k++) { // each block
10 for (char &c : templet->line[i + k][j]) {
11 output[index++] = code[c - '0'];
12 output[index++] = (counter++ < 8) ? ' ' : '
';
13 }
14 }
15 }
16 }
17 output[index++] = '�';
18 fputs(output, fout);
19 }
单车变摩托!但是我觉得还不够好,于是我尝试建立一个buffer,向文件一次性输入1'000'000个字符,将代码变更为:
1 void Template_sudoku::record(FILE* fout, int* index, char buffer[]) {
2 int counter;
3
4 for (int i = 0; i < 8; i += 3) { // each big line
5 for (int j = 0; j < 3; j++) { // each small line
6 counter = 0;
7 for (int k = 0; k < 3; k++) { // each block
8 for (char &c : templet->line[i + k][j]) {
9 if ((*index) >= BUFFER_SIZE - 5) {
10 buffer[(*index)] = '�';
11 fputs(buffer, fout);
12 (*index) = 0;
13 }
14 buffer[(*index)++] = code[c - '0'];
15 buffer[(*index)++] = (counter++ < 8) ? ' ' : '
';
16 }
17 }
18 }
19 }
20 }
21
22 int create_sudoku(int number) {
23 Template_sudoku* tsudo = new Template_sudoku();
24 int counter = 0;
25 FILE* fout = fopen("sudoku.txt", "w");
26 int index = 0;
27 char buffer[BUFFER_SIZE];
28 tsudo->record(fout, &index, buffer);
29 while (tsudo->change2next() && ++counter < number) {
30 buffer[index++] = '
';
31 tsudo->record(fout, &index, buffer);
32 }
33 buffer[index] = '�';
34 fputs(buffer, fout);
35
36 fclose(fout);
37 return 0;
38 }
结果显示为:

图12 第三次分析执行时间5.1秒
solve部分的检测大同小异,只是除了文件IO之外,还需要优化一下vector,将其改成数组,但难度不大。
(9月26日更新)更改了算法,原来是每一次new一个新的数独,这次是只在原数独上进行更改,添加了cancel_certain函数,优化了new运算符带来的时间,注释部分为原来的代码:
1 bool guess_value(Box* box, Subject_sudoku* sudoku, FILE* fout) {
2 //cout << "guess" << endl;
3 int rowno = box->row->number;
4 int columnno = box->column->number;
5 for (int i = 0; i < SIZE; i++) {
6 if (box->posvalue & get_valuebit(i)) { // -- value i+1 is possible
7 //Subject_sudoku* new_sudoku = new Subject_sudoku(*sudoku);
8 Box* box = sudoku->getbox(rowno, columnno);
9 int members_posvalues[3][9]; // NEW
10 int posvalue = box->make_certain(i + 1, members_posvalues);
11 if (fill_sudoku(sudoku, fout)) {
12 return true;
13 }
14 //delete(new_sudoku);
15 box->cancel_certain(posvalue, members_posvalues); // NEW
16 }
17 }
18 return false;
19 }
七、关键代码讲解
关于数独的生成(create)
这一部分是模板的变换,改变模板R4~R9的排列,共有6*6=36种变形,但我们只会用到25种。变换的时候主要是对一个“位置码”进行变换,而不是直接对字符串进行变换:
1 bool Templet::change2next() {
2 if (!next_permutation(line2_position_code.begin(), line2_position_code.end())) {
3 next_permutation(line3_position_code.begin(), line3_position_code.end());
4 sort(line2_position_code.begin(), line2_position_code.end()); // initial line2 code
5 fill_line2();
6 fill_line3();
7 }
8 else {
9 fill_line2();
10 }
11 return true;
12 }
这一部分是数字的变换,和模板变换类似,都用到了next_permutation函数,而且这里也是对“码”(数字码)进行变换:
1 bool Template_sudoku::change2next() {
2 if (!next_permutation(code.begin() + 1, code.end())) {
3 templet->change2next();
4 sort(code.begin() + 1, code.end());
5 }
6 return true;
7 }
以下是填入数字部分的代码,其中c是模板中的数字字符,code是“数字码”,只要将模板的数字字符转化为数字作为下标,从“数字码”中取数字就可以了:
1 buffer[(*index)++] = code[c - '0'];
2 buffer[(*index)++] = (counter++ < 8) ? ' ' : '
';
关于数独的解决(solve)
Box通过make_certain方法确定自己的数字,再将结果传递给所在的Group:
1 void Box::cancel_certain(int posvalue, int members_posvalues[3][9]) {
2 this->row->cancel_certain(this);
3 this->column->cancel_certain(this);
4 this->block->cancel_certain(this);
5 for (int i = 0; i < 9; i++) {
6 this->row->members[i]->posvalue = members_posvalues[0][i];
7 this->column->members[i]->posvalue = members_posvalues[1][i];
8 this->block->members[i]->posvalue = members_posvalues[2][i];
9 }
10
11 this->posvalue = posvalue;
12 this->cervalue = 0;
13 }
Group对成员的可能取值进行更新:
1 void Group::refresh_pos() {
2 for (size_t i = 0; i < SIZE; i++) {
3 members[i]->posvalue &= (~hasvalues); // -- remove impossible value bit
4 }
5 }
对某个Box的值进行猜测:
1 bool guess_value(Box* box, Subject_sudoku* sudoku, FILE* fout) {
2 //cout << "guess" << endl;
3 int rowno = box->row->number;
4 int columnno = box->column->number;
5 for (int i = 0; i < SIZE; i++) {
6 if (box->posvalue & get_valuebit(i)) { // -- value i+1 is possible
7 //Subject_sudoku* new_sudoku = new Subject_sudoku(*sudoku);
8 Box* box = sudoku->getbox(rowno, columnno);
9 int members_posvalues[3][9]; // NEW
10 int posvalue = box->make_certain(i + 1, members_posvalues);
11 if (fill_sudoku(sudoku, fout)) {
12 return true;
13 }
14 //delete(new_sudoku);
15 box->cancel_certain(posvalue, members_posvalues); // NEW
16 }
17 }
18 return false;
19 }
八、实际花费时间
|
PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
|
|
|
· Estimate |
· 估计这个任务需要多少时间 |
5 |
10 |
|
Development |
开发 |
|
|
|
· Analysis |
· 需求分析 (包括学习新技术) |
10 |
10 |
|
· Design Spec |
· 生成设计文档 |
60 |
200 |
|
· Design Review |
· 设计复审 (和同事审核设计文档) |
0 |
0 |
|
· Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
0 |
0 |
|
· Design |
· 具体设计 |
20 |
60 |
|
· Coding |
· 具体编码 |
720 |
590 |
|
· Code Review |
· 代码复审 |
20 |
10 |
|
· Test |
· 测试(自我测试,修改代码,提交修改) |
200 |
600 |
|
Reporting |
报告 |
|
|
|
· Test Report |
· 测试报告 |
60 |
30 |
|
· Size Measurement |
· 计算工作量 |
10 |
10 |
|
· Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
30 |
20 |
|
|
合计 |
1075 |
1540 |
九、小结
这次作业我的收获还是蛮大的,主要体现在理解了优化的重要性。实际上,实现这次功能并不难,难就难在怎么完成地又快又对,这是最花时间的事情。在这一周中,我理解了单元测试,明白了代码检测和优化,并自学QT并完成了一个GUI,成就感颇丰。但愿这一周的努力能为接下来的学习打下基础。
