HDU2489 Minimal Ratio Tree 【DFS】+【最小生成树Prim】

Minimal Ratio Tree

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 2382    Accepted Submission(s): 709

Problem Description

For a tree, which nodes and edges are all weighted, the ratio of it is calculated according to the following equation.




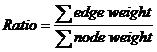
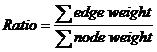
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.

 

Input

Input contains multiple test cases. The first line of each test case contains two integers n (2<=n<=15) and m (2<=m<=n), which stands for the number of nodes in the graph and the number of nodes in the minimal ratio tree. Two zeros end the input. The next line contains n numbers which stand for the weight of each node. The following n lines contain a diagonally symmetrical n×n connectivity matrix with each element shows the weight of the edge connecting one node with another. Of course, the diagonal will be all 0, since there is no edge connecting a node with itself.



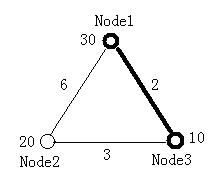
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].

The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.

 

Output

For each test case output one line contains a sequence of the m nodes which constructs the minimal ratio tree. Nodes should be arranged in ascending order. If there are several such sequences, pick the one which has the smallest node number; if there's a tie, look at the second smallest node number, etc. Please note that the nodes are numbered from 1 .

 

Sample Input

3 2
30 20 10
0 6 2
6 0 3
2 3 0
2 2
1 1
0 2
2 0
0 0

 

Sample Output

1 3
1 2

 

Source

2008 Asia Regional Beijing 

⊙﹏⊙‖∣在推断两浮点数大小时应该这样比較：a-b<-(1e-8)；我由于不知道这个WA了6次。

题意：求一个稍微变形的“最小生成树”，其值为边权和除以点权和。

题解：用深搜在n个点里选出m个点。再求这m个点的“最小生成树”就可以。

#include <stdio.h>
#include <string.h>
#include <limits.h>
#define maxn 16

int map[maxn][maxn], node[maxn];
int n, m, store[maxn], vis[maxn];
double ans;
bool visted[maxn]; //hash to vis array

double prim()
{
	int i, j, u, count = 0, tmp, vnv = 0, vne = 0;
	for(i = 1; i <= m; ++i) vnv += node[vis[i]];
	memset(visted, 0, sizeof(visted));
	visted[1] = 1;
	while(count < m - 1){
		for(i = 1, tmp = INT_MAX; i <= m; ++i){
			if(!visted[i]) continue;
			for(j = 1; j <= m; ++j){
				if(!visted[j] && map[vis[i]][vis[j]] < tmp){
					tmp = map[vis[i]][vis[j]]; u = j;
				}
			}
		}
		if(tmp != INT_MAX){
			visted[u] = 1;
			vne += tmp; ++count;
		}
	}
	return vne * 1.0 / vnv;
}

void DFS(int k, int id)
{
	if(id > m){
		double tmp = prim();
		if(tmp - ans < -(1e-8)){
			ans = tmp; memcpy(store, vis, sizeof(vis));
		}
		return;
	}
	for(int i = k; i <= n; ++i){
		vis[id] = i;
		DFS(i + 1, id + 1);
	}
}

int main()
{
	int i, j;
	while(scanf("%d%d", &n, &m), n || m){
		for(i = 1; i <= n; ++i) scanf("%d", &node[i]);
		for(i = 1; i <= n; ++i)
			for(j = 1; j <= n; ++j)
				scanf("%d", &map[i][j]);
		ans = INT_MAX;
		DFS(1, 1);
		for(i = 1; i <= m; ++i)
			if(i != m) printf("%d ", store[i]);
			else printf("%d
", store[i]);
	}
	return 0;
}