概要
上一章介绍了"二叉查找树的相关理论知识,并通过C语言实现了二叉查找树"。这一章给出二叉查找树的C++版本。这里不再对树的相关概念进行介绍,若遇到不明白的概念,可以在上一章查找。
目录
1. 二叉树查找树
2. 二叉查找树的C++实现
3. 二叉查找树的C++实现(完整源码)
4. 二叉查找树的C++测试程序
转载请注明出处:http://www.cnblogs.com/skywang12345/p/3576373.html
更多内容: 数据结构与算法系列 目录
(01) 二叉查找树(一)之 图文解析 和 C语言的实现
(02) 二叉查找树(二)之 C++的实现
(03) 二叉查找树(三)之 Java的实现
二叉查找树简介
二叉查找树(Binary Search Tree),又被称为二叉搜索树。
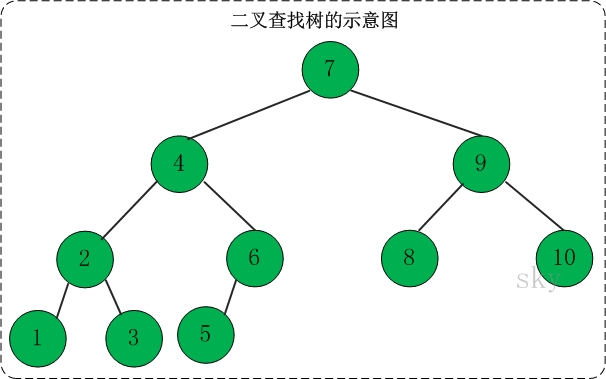
它是特殊的二叉树:对于二叉树,假设x为二叉树中的任意一个结点,x节点包含关键字key,节点x的key值记为key[x]。如果y是x的左子树中的一个结点,则key[y] <= key[x];如果y是x的右子树的一个结点,则key[y] >= key[x]。那么,这棵树就是二叉查找树。如下图所示:
在二叉查找树中:
(01) 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(02) 任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(03) 任意节点的左、右子树也分别为二叉查找树。
(04) 没有键值相等的节点(no duplicate nodes)。
二叉查找树的C++实现
1. 节点和二叉查找树的定义
1.1 二叉查找树节点
template <class T> class BSTNode{ public: T key; // 关键字(键值) BSTNode *left; // 左孩子 BSTNode *right; // 右孩子 BSTNode *parent;// 父结点 BSTNode(T value, BSTNode *p, BSTNode *l, BSTNode *r): key(value),parent(),left(l),right(r) {} };
BSTNode是二叉查找树的节点,它包含二叉查找树的几个基本信息:
(01) key -- 它是关键字,是用来对二叉查找树的节点进行排序的。
(02) left -- 它指向当前节点的左孩子。
(03) right -- 它指向当前节点的右孩子。
(04) parent -- 它指向当前节点的父结点。
1.2 二叉树操作
template <class T> class BSTree { private: BSTNode<T> *mRoot; // 根结点 public: BSTree(); ~BSTree(); // 前序遍历"二叉树" void preOrder(); // 中序遍历"二叉树" void inOrder(); // 后序遍历"二叉树" void postOrder(); // (递归实现)查找"二叉树"中键值为key的节点 BSTNode<T>* search(T key); // (非递归实现)查找"二叉树"中键值为key的节点 BSTNode<T>* iterativeSearch(T key); // 查找最小结点:返回最小结点的键值。 T minimum(); // 查找最大结点:返回最大结点的键值。 T maximum(); // 找结点(x)的后继结点。即,查找"二叉树中数据值大于该结点"的"最小结点"。 BSTNode<T>* successor(BSTNode<T> *x); // 找结点(x)的前驱结点。即,查找"二叉树中数据值小于该结点"的"最大结点"。 BSTNode<T>* predecessor(BSTNode<T> *x); // 将结点(key为节点键值)插入到二叉树中 void insert(T key); // 删除结点(key为节点键值) void remove(T key); // 销毁二叉树 void destroy(); // 打印二叉树 void print(); private: // 前序遍历"二叉树" void preOrder(BSTNode<T>* tree) const; // 中序遍历"二叉树" void inOrder(BSTNode<T>* tree) const; // 后序遍历"二叉树" void postOrder(BSTNode<T>* tree) const; // (递归实现)查找"二叉树x"中键值为key的节点 BSTNode<T>* search(BSTNode<T>* x, T key) const; // (非递归实现)查找"二叉树x"中键值为key的节点 BSTNode<T>* iterativeSearch(BSTNode<T>* x, T key) const; // 查找最小结点:返回tree为根结点的二叉树的最小结点。 BSTNode<T>* minimum(BSTNode<T>* tree); // 查找最大结点:返回tree为根结点的二叉树的最大结点。 BSTNode<T>* maximum(BSTNode<T>* tree); // 将结点(z)插入到二叉树(tree)中 void insert(BSTNode<T>* &tree, BSTNode<T>* z); // 删除二叉树(tree)中的结点(z),并返回被删除的结点 BSTNode<T>* remove(BSTNode<T>* &tree, BSTNode<T> *z); // 销毁二叉树 void destroy(BSTNode<T>* &tree); // 打印二叉树 void print(BSTNode<T>* tree, T key, int direction); };
BSTree是二叉树。它包含二叉查找树的根节点和二叉查找树的操作。二叉查找树的操作中有许多重载函数,例如insert()函数,其中一个是内部接口,另一个是提供给外部的接口。
2 遍历
这里讲解前序遍历、中序遍历、后序遍历3种方式。
2.1 前序遍历
若二叉树非空,则执行以下操作:
(01) 访问根结点;
(02) 先序遍历左子树;
(03) 先序遍历右子树。
前序遍历代码
template <class T> void BSTree<T>::preOrder(BSTNode<T>* tree) const { if(tree != NULL) { cout<< tree->key << " " ; preOrder(tree->left); preOrder(tree->right); } } template <class T> void BSTree<T>::preOrder() { preOrder(mRoot); }
2.2 中序遍历
若二叉树非空,则执行以下操作:
(01) 中序遍历左子树;
(02) 访问根结点;
(03) 中序遍历右子树。
中序遍历代码
template <class T> void BSTree<T>::inOrder(BSTNode<T>* tree) const { if(tree != NULL) { inOrder(tree->left); cout<< tree->key << " " ; inOrder(tree->right); } } template <class T> void BSTree<T>::inOrder() { inOrder(mRoot); }
2.3 后序遍历
若二叉树非空,则执行以下操作:
(01) 后序遍历左子树;
(02) 后序遍历右子树;
(03) 访问根结点。
后序遍历代码
template <class T> void BSTree<T>::postOrder(BSTNode<T>* tree) const { if(tree != NULL) { postOrder(tree->left); postOrder(tree->right); cout<< tree->key << " " ; } } template <class T> void BSTree<T>::postOrder() { postOrder(mRoot); }
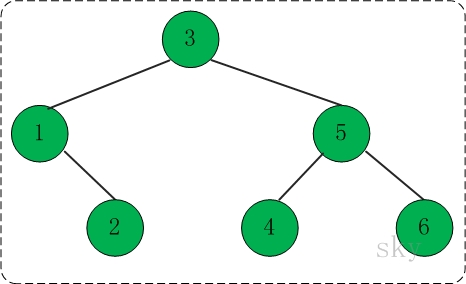
看看下面这颗树的各种遍历方式:
对于上面的二叉树而言,
(01) 前序遍历结果: 3 1 2 5 4 6
(02) 中序遍历结果: 1 2 3 4 5 6
(03) 后序遍历结果: 2 1 4 6 5 3
3. 查找
递归版本的代码
template <class T> BSTNode<T>* BSTree<T>::search(BSTNode<T>* x, T key) const { if (x==NULL || x->key==key) return x; if (key < x->key) return search(x->left, key); else return search(x->right, key); } template <class T> BSTNode<T>* BSTree<T>::search(T key) { search(mRoot, key); }
非递归版本的代码
template <class T> BSTNode<T>* BSTree<T>::iterativeSearch(BSTNode<T>* x, T key) const { while ((x!=NULL) && (x->key!=key)) { if (key < x->key) x = x->left; else x = x->right; } return x; } template <class T> BSTNode<T>* BSTree<T>::iterativeSearch(T key) { iterativeSearch(mRoot, key); }
4. 最大值和最小值
查找最大值的代码
template <class T> BSTNode<T>* BSTree<T>::maximum(BSTNode<T>* tree) { if (tree == NULL) return NULL; while(tree->right != NULL) tree = tree->right; return tree; } template <class T> T BSTree<T>::maximum() { BSTNode<T> *p = maximum(mRoot); if (p != NULL) return p->key; return (T)NULL; }
查找最小值的代码
template <class T> BSTNode<T>* BSTree<T>::minimum(BSTNode<T>* tree) { if (tree == NULL) return NULL; while(tree->left != NULL) tree = tree->left; return tree; } template <class T> T BSTree<T>::minimum() { BSTNode<T> *p = minimum(mRoot); if (p != NULL) return p->key; return (T)NULL; }
5. 前驱和后继
节点的前驱:是该节点的左子树中的最大节点。
节点的后继:是该节点的右子树中的最小节点。
查找前驱节点的代码
/* * 找结点(x)的前驱结点。即,查找"二叉树中数据值小于该结点"的"最大结点"。 */ template <class T> BSTNode<T>* BSTree<T>::predecessor(BSTNode<T> *x) { // 如果x存在左孩子,则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。 if (x->left != NULL) return maximum(x->left); // 如果x没有左孩子。则x有以下两种可能: // (01) x是"一个右孩子",则"x的前驱结点"为 "它的父结点"。 // (01) x是"一个左孩子",则查找"x的最低的父结点,并且该父结点要具有右孩子",找到的这个"最低的父结点"就是"x的前驱结点"。 BSTNode<T>* y = x->parent; while ((y!=NULL) && (x==y->left)) { x = y; y = y->parent; } return y; }
查找后继节点的代码
/* * 找结点(x)的后继结点。即,查找"二叉树中数据值大于该结点"的"最小结点"。 */ template <class T> BSTNode<T>* BSTree<T>::successor(BSTNode<T> *x) { // 如果x存在右孩子,则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。 if (x->right != NULL) return minimum(x->right); // 如果x没有右孩子。则x有以下两种可能: // (01) x是"一个左孩子",则"x的后继结点"为 "它的父结点"。 // (02) x是"一个右孩子",则查找"x的最低的父结点,并且该父结点要具有左孩子",找到的这个"最低的父结点"就是"x的后继结点"。 BSTNode<T>* y = x->parent; while ((y!=NULL) && (x==y->right)) { x = y; y = y->parent; } return y; }
6. 插入
插入节点的代码
/* * 将结点插入到二叉树中 * * 参数说明: * tree 二叉树的根结点 * z 插入的结点 */ template <class T> void BSTree<T>::insert(BSTNode<T>* &tree, BSTNode<T>* z) { BSTNode<T> *y = NULL; BSTNode<T> *x = tree; // 查找z的插入位置 while (x != NULL) { y = x; if (z->key < x->key) x = x->left; else x = x->right; } z->parent = y; if (y==NULL) tree = z; else if (z->key < y->key) y->left = z; else y->right = z; } /* * 将结点(key为节点键值)插入到二叉树中 * * 参数说明: * tree 二叉树的根结点 * key 插入结点的键值 */ template <class T> void BSTree<T>::insert(T key) { BSTNode<T> *z=NULL; // 如果新建结点失败,则返回。 if ((z=new BSTNode<T>(key,NULL,NULL,NULL)) == NULL) return ; insert(mRoot, z); }
注:本文实现的二叉查找树是允许插入相同键值的节点的。若想禁止二叉查找树中插入相同键值的节点,可以参考"二叉查找树(一)之 图文解析 和 C语言的实现"中的插入函数进行修改。
7. 删除
删除节点的代码
/* * 删除结点(z),并返回被删除的结点 * * 参数说明: * tree 二叉树的根结点 * z 删除的结点 */ template <class T> BSTNode<T>* BSTree<T>::remove(BSTNode<T>* &tree, BSTNode<T> *z) { BSTNode<T> *x=NULL; BSTNode<T> *y=NULL; if ((z->left == NULL) || (z->right == NULL) ) y = z; else y = successor(z); if (y->left != NULL) x = y->left; else x = y->right; if (x != NULL) x->parent = y->parent; if (y->parent == NULL) tree = x; else if (y == y->parent->left) y->parent->left = x; else y->parent->right = x; if (y != z) z->key = y->key; return y; } /* * 删除结点(z),并返回被删除的结点 * * 参数说明: * tree 二叉树的根结点 * z 删除的结点 */ template <class T> void BSTree<T>::remove(T key) { BSTNode<T> *z, *node; if ((z = search(mRoot, key)) != NULL) if ( (node = remove(mRoot, z)) != NULL) delete node; }
8. 打印
打印二叉查找树的代码
/* * 打印"二叉查找树" * * key -- 节点的键值 * direction -- 0,表示该节点是根节点; * -1,表示该节点是它的父结点的左孩子; * 1,表示该节点是它的父结点的右孩子。 */ template <class T> void BSTree<T>::print(BSTNode<T>* tree, T key, int direction) { if(tree != NULL) { if(direction==0) // tree是根节点 cout << setw(2) << tree->key << " is root" << endl; else // tree是分支节点 cout << setw(2) << tree->key << " is " << setw(2) << key << "'s " << setw(12) << (direction==1?"right child" : "left child") << endl; print(tree->left, tree->key, -1); print(tree->right,tree->key, 1); } } template <class T> void BSTree<T>::print() { if (mRoot != NULL) print(mRoot, mRoot->key, 0); }
9. 销毁
销毁二叉查找树的代码
/* * 销毁二叉树 */ template <class T> void BSTree<T>::destroy(BSTNode<T>* &tree) { if (tree==NULL) return ; if (tree->left != NULL) return destroy(tree->left); if (tree->right != NULL) return destroy(tree->right); delete tree; tree=NULL; } template <class T> void BSTree<T>::destroy() { destroy(mRoot); }
二叉查找树的C++实现(完整源码)
二叉查找树的C++实现文件(BSTree.h)

1 /** 2 * C++ 语言: 二叉查找树 3 * 4 * @author skywang 5 * @date 2013/11/07 6 */ 7 8 #ifndef _BINARY_SEARCH_TREE_HPP_ 9 #define _BINARY_SEARCH_TREE_HPP_ 10 11 #include <iomanip> 12 #include <iostream> 13 using namespace std; 14 15 template <class T> 16 class BSTNode{ 17 public: 18 T key; // 关键字(键值) 19 BSTNode *left; // 左孩子 20 BSTNode *right; // 右孩子 21 BSTNode *parent;// 父结点 22 23 BSTNode(T value, BSTNode *p, BSTNode *l, BSTNode *r): 24 key(value),parent(),left(l),right(r) {} 25 }; 26 27 template <class T> 28 class BSTree { 29 private: 30 BSTNode<T> *mRoot; // 根结点 31 32 public: 33 BSTree(); 34 ~BSTree(); 35 36 // 前序遍历"二叉树" 37 void preOrder(); 38 // 中序遍历"二叉树" 39 void inOrder(); 40 // 后序遍历"二叉树" 41 void postOrder(); 42 43 // (递归实现)查找"二叉树"中键值为key的节点 44 BSTNode<T>* search(T key); 45 // (非递归实现)查找"二叉树"中键值为key的节点 46 BSTNode<T>* iterativeSearch(T key); 47 48 // 查找最小结点:返回最小结点的键值。 49 T minimum(); 50 // 查找最大结点:返回最大结点的键值。 51 T maximum(); 52 53 // 找结点(x)的后继结点。即,查找"二叉树中数据值大于该结点"的"最小结点"。 54 BSTNode<T>* successor(BSTNode<T> *x); 55 // 找结点(x)的前驱结点。即,查找"二叉树中数据值小于该结点"的"最大结点"。 56 BSTNode<T>* predecessor(BSTNode<T> *x); 57 58 // 将结点(key为节点键值)插入到二叉树中 59 void insert(T key); 60 61 // 删除结点(key为节点键值) 62 void remove(T key); 63 64 // 销毁二叉树 65 void destroy(); 66 67 // 打印二叉树 68 void print(); 69 private: 70 // 前序遍历"二叉树" 71 void preOrder(BSTNode<T>* tree) const; 72 // 中序遍历"二叉树" 73 void inOrder(BSTNode<T>* tree) const; 74 // 后序遍历"二叉树" 75 void postOrder(BSTNode<T>* tree) const; 76 77 // (递归实现)查找"二叉树x"中键值为key的节点 78 BSTNode<T>* search(BSTNode<T>* x, T key) const; 79 // (非递归实现)查找"二叉树x"中键值为key的节点 80 BSTNode<T>* iterativeSearch(BSTNode<T>* x, T key) const; 81 82 // 查找最小结点:返回tree为根结点的二叉树的最小结点。 83 BSTNode<T>* minimum(BSTNode<T>* tree); 84 // 查找最大结点:返回tree为根结点的二叉树的最大结点。 85 BSTNode<T>* maximum(BSTNode<T>* tree); 86 87 // 将结点(z)插入到二叉树(tree)中 88 void insert(BSTNode<T>* &tree, BSTNode<T>* z); 89 90 // 删除二叉树(tree)中的结点(z),并返回被删除的结点 91 BSTNode<T>* remove(BSTNode<T>* &tree, BSTNode<T> *z); 92 93 // 销毁二叉树 94 void destroy(BSTNode<T>* &tree); 95 96 // 打印二叉树 97 void print(BSTNode<T>* tree, T key, int direction); 98 }; 99 100 /* 101 * 构造函数 102 */ 103 template <class T> 104 BSTree<T>::BSTree():mRoot(NULL) 105 { 106 } 107 108 /* 109 * 析构函数 110 */ 111 template <class T> 112 BSTree<T>::~BSTree() 113 { 114 destroy(); 115 } 116 117 /* 118 * 前序遍历"二叉树" 119 */ 120 template <class T> 121 void BSTree<T>::preOrder(BSTNode<T>* tree) const 122 { 123 if(tree != NULL) 124 { 125 cout<< tree->key << " " ; 126 preOrder(tree->left); 127 preOrder(tree->right); 128 } 129 } 130 131 template <class T> 132 void BSTree<T>::preOrder() 133 { 134 preOrder(mRoot); 135 } 136 137 /* 138 * 中序遍历"二叉树" 139 */ 140 template <class T> 141 void BSTree<T>::inOrder(BSTNode<T>* tree) const 142 { 143 if(tree != NULL) 144 { 145 inOrder(tree->left); 146 cout<< tree->key << " " ; 147 inOrder(tree->right); 148 } 149 } 150 151 template <class T> 152 void BSTree<T>::inOrder() 153 { 154 inOrder(mRoot); 155 } 156 157 /* 158 * 后序遍历"二叉树" 159 */ 160 template <class T> 161 void BSTree<T>::postOrder(BSTNode<T>* tree) const 162 { 163 if(tree != NULL) 164 { 165 postOrder(tree->left); 166 postOrder(tree->right); 167 cout<< tree->key << " " ; 168 } 169 } 170 171 template <class T> 172 void BSTree<T>::postOrder() 173 { 174 postOrder(mRoot); 175 } 176 177 /* 178 * (递归实现)查找"二叉树x"中键值为key的节点 179 */ 180 template <class T> 181 BSTNode<T>* BSTree<T>::search(BSTNode<T>* x, T key) const 182 { 183 if (x==NULL || x->key==key) 184 return x; 185 186 if (key < x->key) 187 return search(x->left, key); 188 else 189 return search(x->right, key); 190 } 191 192 template <class T> 193 BSTNode<T>* BSTree<T>::search(T key) 194 { 195 search(mRoot, key); 196 } 197 198 /* 199 * (非递归实现)查找"二叉树x"中键值为key的节点 200 */ 201 template <class T> 202 BSTNode<T>* BSTree<T>::iterativeSearch(BSTNode<T>* x, T key) const 203 { 204 while ((x!=NULL) && (x->key!=key)) 205 { 206 if (key < x->key) 207 x = x->left; 208 else 209 x = x->right; 210 } 211 212 return x; 213 } 214 215 template <class T> 216 BSTNode<T>* BSTree<T>::iterativeSearch(T key) 217 { 218 iterativeSearch(mRoot, key); 219 } 220 221 /* 222 * 查找最小结点:返回tree为根结点的二叉树的最小结点。 223 */ 224 template <class T> 225 BSTNode<T>* BSTree<T>::minimum(BSTNode<T>* tree) 226 { 227 if (tree == NULL) 228 return NULL; 229 230 while(tree->left != NULL) 231 tree = tree->left; 232 return tree; 233 } 234 235 template <class T> 236 T BSTree<T>::minimum() 237 { 238 BSTNode<T> *p = minimum(mRoot); 239 if (p != NULL) 240 return p->key; 241 242 return (T)NULL; 243 } 244 245 /* 246 * 查找最大结点:返回tree为根结点的二叉树的最大结点。 247 */ 248 template <class T> 249 BSTNode<T>* BSTree<T>::maximum(BSTNode<T>* tree) 250 { 251 if (tree == NULL) 252 return NULL; 253 254 while(tree->right != NULL) 255 tree = tree->right; 256 return tree; 257 } 258 259 template <class T> 260 T BSTree<T>::maximum() 261 { 262 BSTNode<T> *p = maximum(mRoot); 263 if (p != NULL) 264 return p->key; 265 266 return (T)NULL; 267 } 268 269 /* 270 * 找结点(x)的后继结点。即,查找"二叉树中数据值大于该结点"的"最小结点"。 271 */ 272 template <class T> 273 BSTNode<T>* BSTree<T>::successor(BSTNode<T> *x) 274 { 275 // 如果x存在右孩子,则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。 276 if (x->right != NULL) 277 return minimum(x->right); 278 279 // 如果x没有右孩子。则x有以下两种可能: 280 // (01) x是"一个左孩子",则"x的后继结点"为 "它的父结点"。 281 // (02) x是"一个右孩子",则查找"x的最低的父结点,并且该父结点要具有左孩子",找到的这个"最低的父结点"就是"x的后继结点"。 282 BSTNode<T>* y = x->parent; 283 while ((y!=NULL) && (x==y->right)) 284 { 285 x = y; 286 y = y->parent; 287 } 288 289 return y; 290 } 291 292 /* 293 * 找结点(x)的前驱结点。即,查找"二叉树中数据值小于该结点"的"最大结点"。 294 */ 295 template <class T> 296 BSTNode<T>* BSTree<T>::predecessor(BSTNode<T> *x) 297 { 298 // 如果x存在左孩子,则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。 299 if (x->left != NULL) 300 return maximum(x->left); 301 302 // 如果x没有左孩子。则x有以下两种可能: 303 // (01) x是"一个右孩子",则"x的前驱结点"为 "它的父结点"。 304 // (01) x是"一个左孩子",则查找"x的最低的父结点,并且该父结点要具有右孩子",找到的这个"最低的父结点"就是"x的前驱结点"。 305 BSTNode<T>* y = x->parent; 306 while ((y!=NULL) && (x==y->left)) 307 { 308 x = y; 309 y = y->parent; 310 } 311 312 return y; 313 } 314 315 /* 316 * 将结点插入到二叉树中 317 * 318 * 参数说明: 319 * tree 二叉树的根结点 320 * z 插入的结点 321 */ 322 template <class T> 323 void BSTree<T>::insert(BSTNode<T>* &tree, BSTNode<T>* z) 324 { 325 BSTNode<T> *y = NULL; 326 BSTNode<T> *x = tree; 327 328 // 查找z的插入位置 329 while (x != NULL) 330 { 331 y = x; 332 if (z->key < x->key) 333 x = x->left; 334 else 335 x = x->right; 336 } 337 338 z->parent = y; 339 if (y==NULL) 340 tree = z; 341 else if (z->key < y->key) 342 y->left = z; 343 else 344 y->right = z; 345 } 346 347 /* 348 * 将结点(key为节点键值)插入到二叉树中 349 * 350 * 参数说明: 351 * tree 二叉树的根结点 352 * key 插入结点的键值 353 */ 354 template <class T> 355 void BSTree<T>::insert(T key) 356 { 357 BSTNode<T> *z=NULL; 358 359 // 如果新建结点失败,则返回。 360 if ((z=new BSTNode<T>(key,NULL,NULL,NULL)) == NULL) 361 return ; 362 363 insert(mRoot, z); 364 } 365 366 /* 367 * 删除结点(z),并返回被删除的结点 368 * 369 * 参数说明: 370 * tree 二叉树的根结点 371 * z 删除的结点 372 */ 373 template <class T> 374 BSTNode<T>* BSTree<T>::remove(BSTNode<T>* &tree, BSTNode<T> *z) 375 { 376 BSTNode<T> *x=NULL; 377 BSTNode<T> *y=NULL; 378 379 if ((z->left == NULL) || (z->right == NULL) ) 380 y = z; 381 else 382 y = successor(z); 383 384 if (y->left != NULL) 385 x = y->left; 386 else 387 x = y->right; 388 389 if (x != NULL) 390 x->parent = y->parent; 391 392 if (y->parent == NULL) 393 tree = x; 394 else if (y == y->parent->left) 395 y->parent->left = x; 396 else 397 y->parent->right = x; 398 399 if (y != z) 400 z->key = y->key; 401 402 return y; 403 } 404 405 /* 406 * 删除结点(z),并返回被删除的结点 407 * 408 * 参数说明: 409 * tree 二叉树的根结点 410 * z 删除的结点 411 */ 412 template <class T> 413 void BSTree<T>::remove(T key) 414 { 415 BSTNode<T> *z, *node; 416 417 if ((z = search(mRoot, key)) != NULL) 418 if ( (node = remove(mRoot, z)) != NULL) 419 delete node; 420 } 421 422 /* 423 * 销毁二叉树 424 */ 425 template <class T> 426 void BSTree<T>::destroy(BSTNode<T>* &tree) 427 { 428 if (tree==NULL) 429 return ; 430 431 if (tree->left != NULL) 432 return destroy(tree->left); 433 if (tree->right != NULL) 434 return destroy(tree->right); 435 436 delete tree; 437 tree=NULL; 438 } 439 440 template <class T> 441 void BSTree<T>::destroy() 442 { 443 destroy(mRoot); 444 } 445 446 /* 447 * 打印"二叉查找树" 448 * 449 * key -- 节点的键值 450 * direction -- 0,表示该节点是根节点; 451 * -1,表示该节点是它的父结点的左孩子; 452 * 1,表示该节点是它的父结点的右孩子。 453 */ 454 template <class T> 455 void BSTree<T>::print(BSTNode<T>* tree, T key, int direction) 456 { 457 if(tree != NULL) 458 { 459 if(direction==0) // tree是根节点 460 cout << setw(2) << tree->key << " is root" << endl; 461 else // tree是分支节点 462 cout << setw(2) << tree->key << " is " << setw(2) << key << "'s " << setw(12) << (direction==1?"right child" : "left child") << endl; 463 464 print(tree->left, tree->key, -1); 465 print(tree->right,tree->key, 1); 466 } 467 } 468 469 template <class T> 470 void BSTree<T>::print() 471 { 472 if (mRoot != NULL) 473 print(mRoot, mRoot->key, 0); 474 } 475 476 #endif
二叉查找树的C++测试程序(BSTreeTest.cpp)

1 /** 2 * C++ 语言: 二叉查找树 3 * 4 * @author skywang 5 * @date 2013/11/07 6 */ 7 8 #include <iostream> 9 #include "BSTree.h" 10 using namespace std; 11 12 static int arr[]= {1,5,4,3,2,6}; 13 #define TBL_SIZE(a) ( (sizeof(a)) / (sizeof(a[0])) ) 14 15 int main() 16 { 17 int i, ilen; 18 BSTree<int>* tree=new BSTree<int>(); 19 20 cout << "== 依次添加: "; 21 ilen = TBL_SIZE(arr); 22 for(i=0; i<ilen; i++) 23 { 24 cout << arr[i] <<" "; 25 tree->insert(arr[i]); 26 } 27 28 cout << " == 前序遍历: "; 29 tree->preOrder(); 30 31 cout << " == 中序遍历: "; 32 tree->inOrder(); 33 34 cout << " == 后序遍历: "; 35 tree->postOrder(); 36 cout << endl; 37 38 cout << "== 最小值: " << tree->minimum() << endl; 39 cout << "== 最大值: " << tree->maximum() << endl; 40 cout << "== 树的详细信息: " << endl; 41 tree->print(); 42 43 cout << " == 删除根节点: " << arr[3]; 44 tree->remove(arr[3]); 45 46 cout << " == 中序遍历: "; 47 tree->inOrder(); 48 cout << endl; 49 50 // 销毁二叉树 51 tree->destroy(); 52 53 return 0; 54 }
关于二叉查找树的C++实现有两点需要补充说明的:
第1点:采用了STL模板。因此,二叉查找树支持任意数据类型。
第2点:将二叉查找树的"声明"和"实现"都位于BSTree.h中。这是因为,在二叉查找树的实现采用了模板;而C++编译器不支持对模板的分离式编译!
二叉查找树的C++测试程序
上面的BSTreeTest.c是二叉查找树树的测试程序,运行结果如下:
== 依次添加: 1 5 4 3 2 6 == 前序遍历: 1 5 4 3 2 6 == 中序遍历: 1 2 3 4 5 6 == 后序遍历: 2 3 4 6 5 1 == 最小值: 1 == 最大值: 6 == 树的详细信息: 1 is root 5 is 1's right child 4 is 5's left child 3 is 4's left child 2 is 3's left child 6 is 5's right child == 删除根节点: 3 == 中序遍历: 1 2 4 5 6
下面对测试程序的流程进行分析!
(01) 新建"二叉查找树"root。
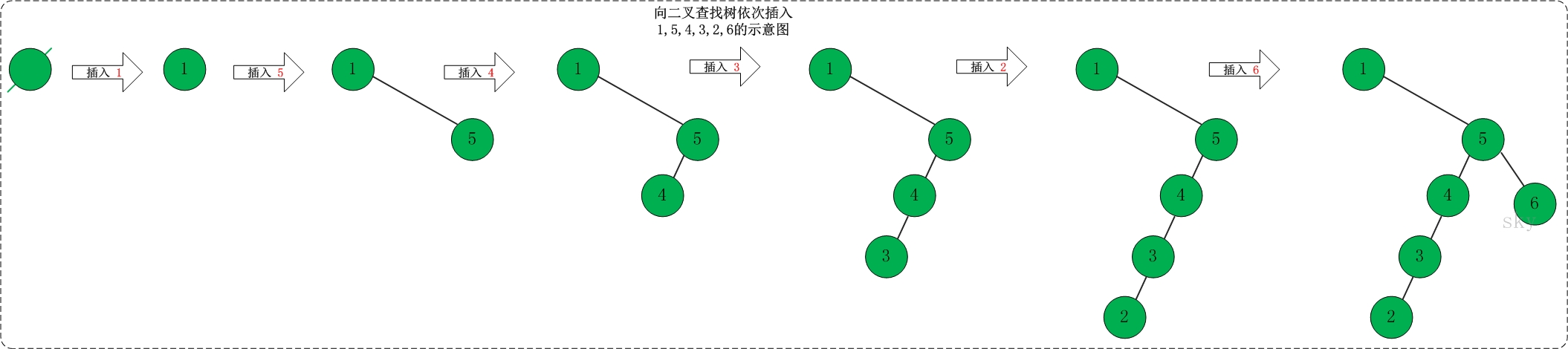
(02) 向二叉查找树中依次插入1,5,4,3,2,6 。如下图所示:
(03) 遍历和查找
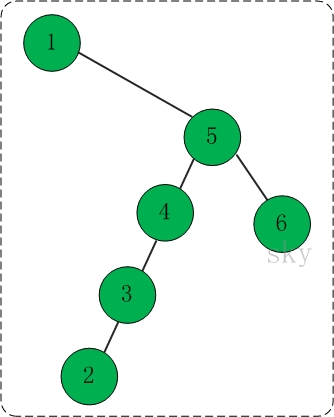
插入1,5,4,3,2,6之后,得到的二叉查找树如下:
前序遍历结果: 1 5 4 3 2 6
中序遍历结果: 1 2 3 4 5 6
后序遍历结果: 2 3 4 6 5 1
最小值是1,而最大值是6。
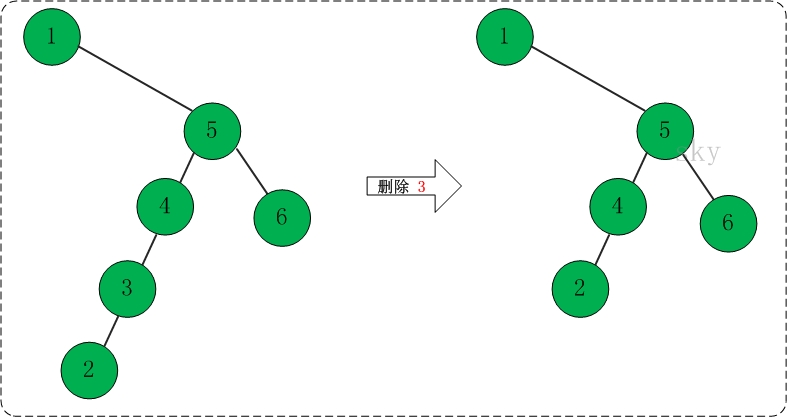
(04) 删除节点4。如下图所示:
(05) 重新遍历该二叉查找树。
中序遍历结果: 1 2 4 5 6