Codechef April Challenge 2019 游记
Subtree Removal
题目大意:
一棵(n(nle10^5))个结点的有根树,每个结点有一个权值(w_i(|w_ile10^9|))。你可以进行若干次(包括(0)次)操作,每次你可以选择一个连通块,将其删去。若你的操作次数为(k),则总收益为剩下结点权值之和(-Xcdot k)。求最大总收益。
思路:
树形DP,(f_x)表示以(x)为根的子树的最大总收益。转移时(f_x=w_x+sum_{yin{ m children}_x}f_y)。若(f_x<-X),则令(f_x=-X)。
时间复杂度(mathcal O(n))。
源代码见提交记录。
Playing with Numbers
题目大意:
一棵(n(nle10^5))个结点的有根树,每个结点有一个权值(v_i)和一个额外的属性(m_i)。对于一个叶子结点(l_i),定义其答案为:
- 对于从根节点到(l_i)的路径上的每个节点,选择一个非负整数,乘以节点的点权。
- 对路径上所有节点按照上述方式算出来的值求和。
- 叶子(l_i)的答案就是和对(m_{l_i})取模的最大值。
求每个叶子节点的答案。
思路:
一个结论是,若干个数({A_1,A_2,ldots,A_k})在模(m)意义下,能组合出的最大数为(m-gcd(A_1,A_2,ldots,A_k,m))。
只需一次DFS求出(l_i)到根结点链上的(gcd),然后套用上述结论即可。
时间复杂度(mathcal O(nlog v_i))。
源代码见提交记录。
Kira Loves Palindromes
题目大意:
给定字符串(S(|S|le1000,S_iin[ exttt{'a'}, exttt{'z'}])),请求出有多少种方案可以从该字符串中选出两个不相交的非空子串(记为(s_1)和(s_2)),使得其串接(s_1+s_2)为回文串。
我们认为((s_1,s_2))和((s^′_1,s^′_2))是不同的两种方案,当且仅当(s_1)和(s^′_1)的位置不同,或者(s_2)和(s^′_2)的位置不同。
思路:
如图所示:
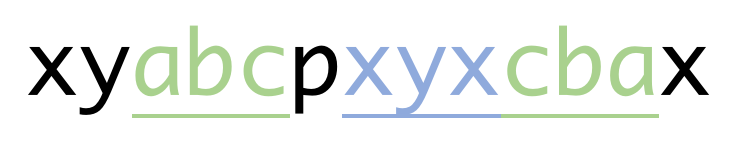
(s_1= exttt{'abc'},s_2= exttt{'xyxcba'}),其中( exttt{'abc'})和( exttt{'cba'})是对应的部分,而( exttt{'xyx'})是插入在中间的回文串。
枚举两个( exttt{'c'})的位置(p)和(q),二分出从(p)和(q)往两侧扩展出的最长距离(len),对于插入串(S_{[l,r]}),预处理出满足(l=p+1)且(r<q-1)或(r=q-1)且(l>p+1)的回文串个数(cnt)(注意这里不考虑(l=p+1)且(r=q-1)的情况,避免算重)。对于固定的(p,q),答案为(len imes(cnt+1))((+1)表示插入串为空)。最后将未统计的(l=p+1)且(r=q-1)的情况计入答案即可。
使用字符串哈希算法可以简单地实现。
时间复杂度(mathcal O(n^2log n))。
源代码见提交记录。
Offer for Chef
题目大意:
一个长度为(n(nle10^5))的数列(A_{1sim n}),(q(qle10))次询问,每次给出数列(t_{1sim n})((t_i)中只有不超过(50)个数不为(0))和一个整数(k),问将这个数列分为(k)段,定义每一段的价值为区间内每个元素(A_icdot t_i)之和。总收益为所有区间价值的按位与。最大化总收益。
思路:
原题链接CF981D。
显然我们可以将(A_icdot t_i=0)的数去掉,记剩下数的个数为(m)。
从高到低枚举答案的每一个二进制位,判断是否可以为(1)。若可以,则在保留这一位的情况下处理下一位。判定某一位是否能为(1)可以用一个(mathcal O(m^3))的动态规划实现,这里不再赘述。
大约枚举(60)个二进制位,时间复杂度(mathcal O(60cdot qm^3))。
源代码见提交记录。
Mininum XOR over Tree
题目大意:
给定一棵(n(nle2 imes10^5))的有根树,每个结点有权值(w_i(1le w_i<2^20))。(q(qle10^6))次询问,给定结点(v)和参数(k(qle k<2^20)),求对于子树(v)中所有结点(u),(w_uoplus k)的最大值,并输出使答案最大的编号最小的(u)。强制在线。
思路:
以DFS序为时间,建立可持久化01字典树。查询时就在子树对应的区间内查找能异或出的最大值。
考虑如何根据这个(w_uoplus k)的最大值求出最小的(u)。
将所有结点以(w_i)为第一关键字,DFS序为第二关键字排序。维护区间内结点编号的最小值。询问时由于知道了(w_u),只须在对应权值、对应DFS序的区间内查找最大值即可。这可以用稀疏表方便地实现。
时间复杂度(mathcal O(nlog n+(n+q)log w_i))。
实现上需要注意常数。
源代码见提交记录。