深度强化学习（Deep Reinforcement Learning）入门：RL base & DQN-DDPG-A3C introduction

深度强化学习（Deep Reinforcement Learning）入门：RL base & DQN-DDPG-A3C introduction
转自https://zhuanlan.zhihu.com/p/25239682

过去的一段时间在深度强化学习领域投入了不少精力，工作中也在应用DRL解决业务问题。子曰：温故而知新，在进一步深入研究和应用DRL前，阶段性的整理下相关知识点。本文集中在DRL的model-free方法的Value-based和Policy-base方法，详细介绍下RL的基本概念和Value-based DQN，Policy-based DDPG两个主要算法，对目前state-of-art的算法（A3C）详细介绍，其他前沿算法的详细理解留待后续展开。

一、RL：a simple introduction

强化学习是机器学习的一个分支，相较于机器学习经典的有监督学习、无监督学习问题，强化学习最大的特点是在交互中学习（Learning from Interaction）。Agent在与环境的交互中根据获得的奖励或惩罚不断的学习知识，更加适应环境。RL学习的范式非常类似于我们人类学习知识的过程，也正因此，RL被视为实现通用AI重要途径。

1.1 强化学习问题的基本设定：
```
<A, S, R, P>
Action space : A 
State space : S
Reward: R : S × A × S → R
Transition : P :S × A → S 
```
<A, S, R, P>就是RL中经典的四元组了。A代表的是Agent的所有动作；State是Agent所能感知的世界的状态；Reward是一个实数值，代表奖励或惩罚；P则是Agent所交互世界，也被称为model。基于此以下给出强化学习系统的几个重要概念：
- Policy: Policy是指Agent则是在状态s时，所要做出action的选择，定义为 $pi$ ，是RL中最核心的问题了。policy可以视为在Agent感知到环境后s后到动作a的一个mapping。如果策略是随机的，policy是根据每个动作概率 $pi(a|s)$ 选择动作；如果策略是确定性的，policy则是直接根据状态s选择出动作 $a=pi (s)$ 。
　　　　

　　　　
- Reward Signal：reward signal定义了Agent学习的目标。Agent每一次和环境交互，环境返回reward，告诉Agent刚刚的action是好的，还是不好的，可以理解为对agent的奖励和惩罚，agent与环境交互的序列流见下图。需要注意的是，Reward $e$ Goal！即agent的目标并非当前reward最大，而是平均累计回报最大。
- Value function：Reward Signal定义的是评判一次交互中的立即的（immediate sense）回报好坏。而Value function则定义的是从长期看action平均回报的好坏。比如象棋中，吃掉对方一个“车”的即时收益很大，但如果因为吃“车”，老“将”被对方吃掉，显然长期看吃“车”这个action是不好的。即一个状态s的value是其长期期望Reward的高低。定义是策略状态s长期期望收益，是策略在状态s下，采取动作a的长期期望收益。
  - 　　定义 $G_{t}$ 为长期回报期望（Return）：
- - 状态s的value为：
  - 状态s下采取动作a的Q值为：
  - 其中 $0< gamma <1$ 是长期收益的折扣因子，类似于金融中的折现率
- Model of the environment：model是对真实世界（environment）的模拟，model建模的是agent采样action后环境的反应。RL中，使用model和planning的方法被称为model-based，反之不使用model而是通过try-and-error学习policy的方法被称为model-free。本文范畴即是model-free。
1.2 强化学习：一个MDP（Markov Decision Process）过程：

RL的重要基础是MDP了，其中Markov体现在:

即在状态 $s_{t}$ 时，采取动作 $a_{t}$ 后的状态 $s_{t+1}$ 和收益 $r_{t+1}$ 只与当前状态和动作有关，与历史状态无关。（如果与“历史状态”相关，那么把这个状态封装到 $s_{t}$ 即可了）。而Decision则体现在在每一个状态s处，都是要进行决策采取什么行动，即policy了。

1.3 Bellman等式

Bellman等式是RL最核心的公式了，虽然重要，但推导起来其实非常简单好理解，推导过程就省略了。

Bellman equation

$V_{pi }(s)=sum_{}^{}{pi (a|s) E[R_{t+1}+gamma V(s_{t+1})|S_{t}=s]}$

Bellman optimality equation

$V_{*}(s)=E[R_{t+1}+gamma max_{pi } V(s_{t+1})|S_{t}=s]$
$Q_{*}(s,a)=E[R_{t+1}+gamma max_{a^{'} } Q(s_{t+1}, a^{'} )|S_{t}=s,A_{t}=a]$

1.4 MC、TD

有关RL的基础，再简单介绍下 MC、TD方法，其他内容篇幅原因不再展开了。

Monte-Carlo method适用于“情节式任务”（情节任务序列有终点，与“情节式任务”相对应的是“连续型任务”）。Q(s,a)就是整个序列的期望回报。MC增量更新中的Monte-Carlo error：

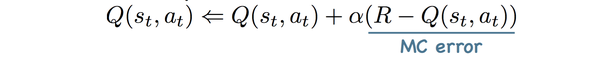
TD（Time Difference） method，是Monte-Carlo和Dynamic Programming 方法的一个结合。相比MC方法，TD除了能够适用于连续任务外，和MC的差异从下图可以清楚看到。MC需要回退整个序列更新Q值，而TD只需要回退1步或n步更新Q值。因为MC需要等待序列结束才能训练，而TD没有这个限制，因此TD收敛速度明显比MC快，目前的主要算法都是基于TD。下图是TD和MC的回退图，很显然MC回退的更深。

直观理解MC error和TD error的差异，假设RL的任务要预估的是上班的"到公司时长"，状态是目前的位置，比如“刚出门”“到地铁了”“到国贸站了”...。MC方法需要等到真正开到公司才能校验“刚出门”状态时预估的正确性，得到MC error；而TD则可以利用“刚出门”和“到地铁了”两个状态预测的差异的1-step TD error来迭代。

1-step TD error：

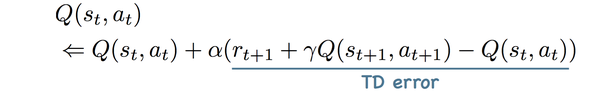
n-steps TD error：

$R^{(n)}=r_{t+1}+gamma r_{t+2}+...+gamma ^{n-2}r_{t+n-1}+gamma ^{n-1}Q(s_{t+n}, a_{t+n})$

$TD(lambda )$ error：

$R^{(lambda )}=(1-lambda )sum_{n}^{i=1}{lambda ^{i}R^{(i)}}$

事实上，MC error可以视为一个情节任务的max-step TD error。另外，一般来说，在TD error中，n越大，用到的真实回报信息更多，收敛也会越快。

二、DRL：from Q-learning to DQN

Q-learning一种TD方法，也是一种Value-based的方法。所谓Value-based方法，就是先评估每个action的Q值(Value)，再根据Q值求最优策略 $pi (a|s)$ 的方法。强化学习的最终目标是求解policy，因此Value-based的方法是一种“曲线救国”。Q-learning算法的核心就是我们1.3中介绍的Bellman optimality equation，即：

$Q_{*}(s,a)=E[R_{t+1}+gamma max_{a^{'} } Q(s_{t+1}, a^{'} )|S_{t}=s,A_{t}=a]$

Q-learning是RL的很经典的算法，但有个很大的问题在于它是一种表格方法，也就是说它非常的直来之前，就是根据过去出现过的状态，统计和迭代Q值。一方面Q-learning适用的状态和动作空间非常小；另一方面但如果一个状态从未出现过，Q-learning是无法处理的。也就是说Q-learning压根没有预测能力，也就是没有泛化能力。

为了能使得Q的学习能够带有预测能力，熟悉机器学习的同学很容易想到这就是一个回归问题啊！用函数拟合Q：

$heta$ 代表的是模型参数，

模型有很多种选择，线性的或非线性的。传统的非深度学习的函数拟合更多是人工特征+线性模型拟合。这几年伴随着深度学习最近几年在监督学习领域的巨大成功，用深度神经网络端到端的拟合Q值，也就是DQN，似乎是个必然了。

deepmind 在2013年的 Playing Atari with Deep Reinforcement Learning 提出的DQN算是DRL的一个重要起点了，也是理解DRL不可错过的经典模型了。网络结构设计方面，DQN之前有些网络是左图的方式，输入为S，A，输出Q值；DQN采用的右图的结构，即输入S，输出是离线的各个动作上的Q值。之所以这样，左图方案相对右图最大的缺点是对于每个state，需要计算 $|A|$ 次前向计算，而右图则只需要一次前向计算即可，因此左图的前向计算成本与action的数量成正比。

论文中，解决的问题是Atari游戏问题，输入数据（状态S）就是游戏原始画面的像素点，动作空间是摇杆方向等。这也是DNN带来的最大好处，有过特征工程经验的同学自然理解，不做特征工程想想都觉得轻松，更不要提效果还能提升了

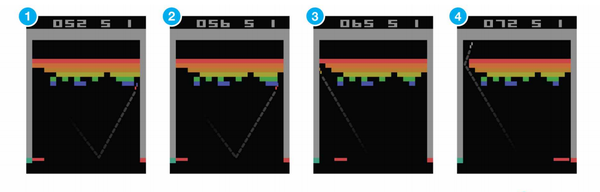
DQN具体的网络结构见下：实际输入是游戏的连续4帧画面，不只使用1帧画面为了感知环境的动态性，接两层CNN，两层FNN，输出各个动作的Q值。

因为DQN本身是个回归问题，模型的优化目标是最小化1-step TD error的平方loss，梯度的计算也很直接了，见下图。

DQN最终能够取得成功的一方面是采用了DNN网络进行Q值的函数拟合，end-to-end的模型训练。更重要的是引入了以下两个点：
- Experience Replay：DeepLearning取得重大进展的监督学习中，样本间都是独立同分布的。而RL中的样本是有关联的，非静态的（highly correlated and non-stationary），训练的结果很容易难以收敛。Experience Replay机制解决这个问题思路其实很简单，构建一个存储把样本都存储下来，通过随机采样去除相关性。（当然没有天下免费的午餐，这种方法也有弊端，比如off-policy受到了限制，也不是真正的online-learning，具体在A3C部分会展开分析）
- separate Target Network：原始的Q-learning中，在1-step TD return，样本标签y使用的是和训练的Q-network相同的网络。这样通常情况下，能够使得Q大的样本，y也会大，这样模型震荡和发散可能性变大。而构建一个独立的慢于当前Q-Network的target Q-Network来计算y，使得训练震荡发散可能性降低，更加稳定。
- 另外，TD-error也被clip到[-1,1]区间，增加模型的稳定性。部分思路和我们后续分享的的TRPO算法的置信区间相关。
详细的DQN算法：

附DQN15年发表在nature的文章 Human-level control through deep reinforcement learning

后续关于DQN有三个主要改进点：
- Double Q-Network：思路并不新鲜，仿照Double Q-learning，一个Q网络用于选择动作，另一个Q网络用于评估动作，交替工作，解决upward-bias问题，效果不错。三个臭皮匠顶个诸葛亮么，就像工作中如果有double-check，犯错的概率就能平方级别下降。Silver15年论文Deep Reinforcement Learning with Double Q-learning
- Prioritized replay：基于优先级的replay机制，replay加速训练过程，变相增加样本，并且能独立于当前训练过程中状态的影响。这个replay权重还是和DQN error（下图）有关，Silver16年论文PRIORITIZED EXPERIENCE REPLAY。
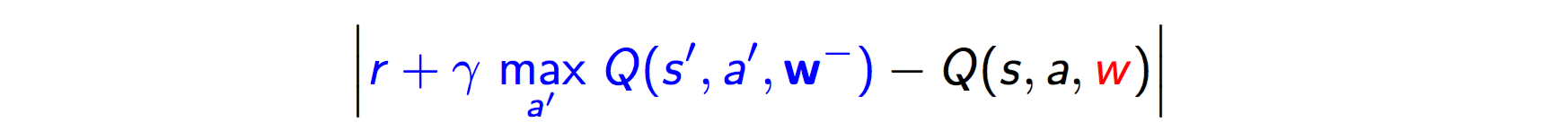
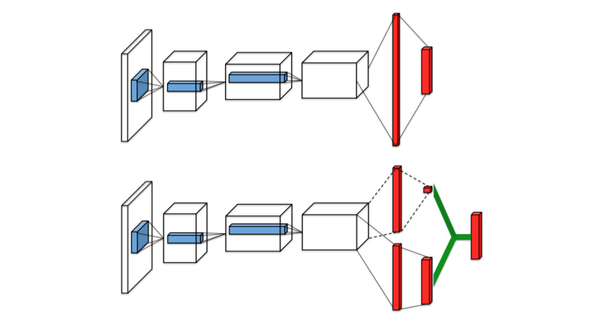
- Dueling network：在网络内部把Q(s,a) 分解成 V(s) + A(s, a)，V(s)与动作无关，A(s, a)与动作相关，是a相对s平均回报的相对好坏，是优势，解决reward-bias问题。RL中真正关心的还是策略的好坏，更关系的是优势，另外在某些情况下，任何策略都不影响回报，显然需要剔除。ICML 2016 Best Paper：DUELING NETWORK ARCHITECTURES FOR DEEP REINFORCEMENT LEARNING 。Dueling Network网络架构如下，Dueling Network把网络分成一个输出标量V(s)另一个输出动作上Advantage值两部分，最后合成Q值。非常巧妙的设计，当然还是end-to-end的，效果也是state-of-art。Advantage是一个比较有意思的问题，A3C中有一个A就是Advantage，计划后面把Advantage单独拉出来研究下单独分享。
三、Policy-Based method：概率输出&连续动作空间

DQN虽然在Atari游戏问题中取得了巨大的成功，但适用范围还是在低维、离散动作空间。DQN是求每个action的 $max_{a} Q(s,a)$ ，在连续空间就不适用了，原因如下：
1. 如果采用把连续动作空间离散化，动作空间则会过大，极难收敛。比如连续动作空间=10，每个动作划分成3个离散动作，动作空间将扩大到 $3^{10}= 59049$ 。而且每个动作空间划分成3个离散动作无法做到fine-tuning，划分本身也带来了信息损失。
2. 即便是有些DQN的变种如VAE能够给出连续动作的方案，DQN的第二个问题是只能给出一个确定性的action，无法给出概率值。而有些场景，比如围棋的开局，只有一种走法显然太死板了，更多例子不再介绍了。
从另外一个角度看，DQN是Value-based方法，上一节讲到了Value-based的方法还是在间接求策略。一个自然的逻辑是为什么我们不直接求解Policy？这就是Policy Gradient方法了。

3.1 策略梯度

策略梯度方法中，参数化策略 $pi$ 为 $pi _{ heta }$ ，然后计算得到动作上策略梯度，沿着梯度方法，一点点的调整动作，逐渐得到最优策略。

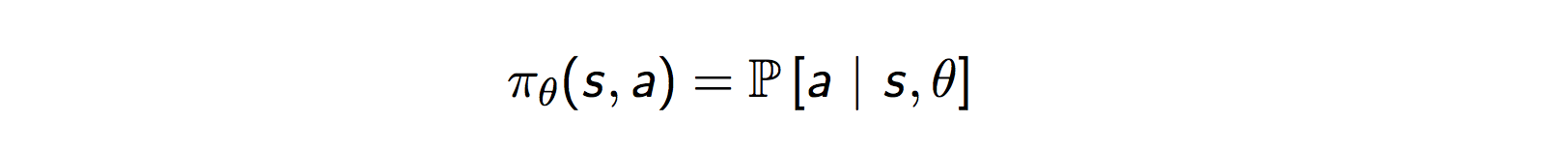
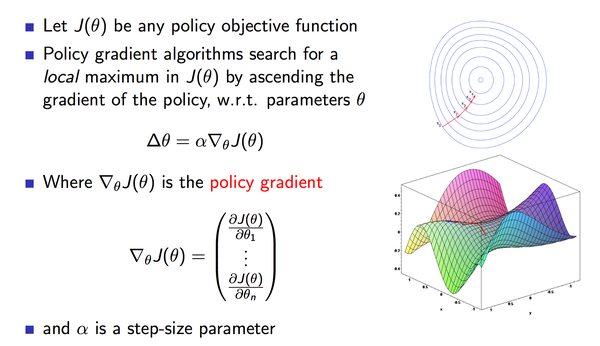
定义 $J( heta )$ 为整体的performance metrics。下图截取的PPT页很好的表达了PG的原理。

3.2 随机和确定性策略梯度

Sutton早在1999年就发表论文Policy Gradient Methods for Reinforcement Learning with Function Approximation证明了随机策略梯度的计算公式：

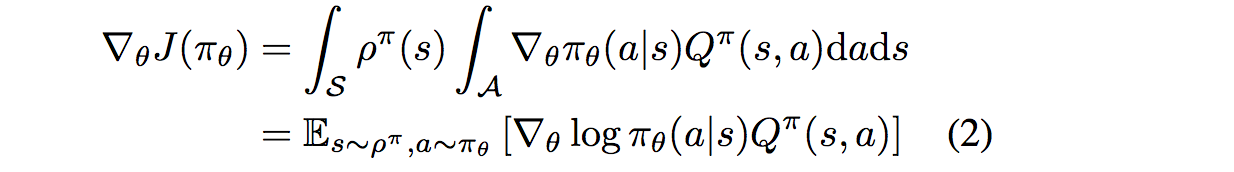
证明过程就不贴了，有兴趣读一下能加深下理解。也可以读读 REINFORCE算法（with or without Baseline）Simple statistical gradient-following algorithms for connectionist reinforcement learning，92年的文章了，略微老了些。

David Silver在14年的论文Deterministic Policy Gradient Algorithms（DPG）证明了DPG的策略梯度公式，结论同样非常简洁：

太理论性的东西不多贴了，有两个点值得注意：
- DPG和随机策略梯度SPG差异在于随机策略梯度中有一个log项，本质上源于随机策略需要重新加一层策略u的期望，导致策略网络u的梯度相对DPG需要除以策略u，数学转化成log(u)的倒数了。这个形式和交叉熵很接近，其实完全可以从概率角度去理解，有物理意义。
- DPG中本质上式在max(Q)，和DQN最终竟还是殊途同归，直观的去理解的话，Policy是按照Q值最大的方向调整policy的参数。
3.3 深度确定性策略梯度

google的这篇DDPG论文CONTINUOUS CONTROL WITH DEEP REINFORCEMENT LEARNING结合了上文中DQN和DPG，把DRL推向了连续动作空间控制。
- actor-critic：在介绍DDPG前，简单的介绍下 actor-critic算法。actor-critic算法是一种TD method。结合了value-based和policy-based方法。policy网络是actor（行动者），输出动作（action-selection）。value网络是critic（评价者），用来评价actor网络所选动作的好坏（action value estimated），并生成TD_error信号同时指导actor网络critic网络的更新。下图为actor-critic算法的一个架构图，DDPG就是这一类算法。
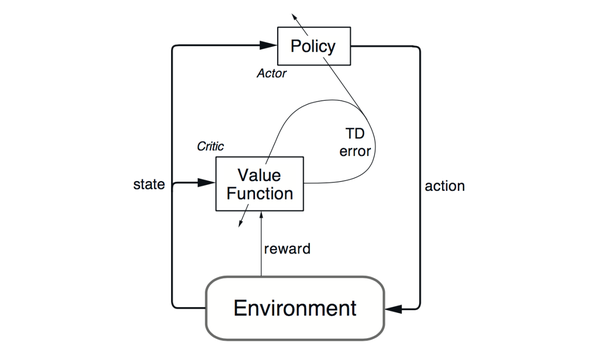
DDPG中，actor网络的输入时state，输出action，以DNN进行函数拟合，对于连续动作NN输出层可以用tanh或sigmod，离散动作以softmax作为输出层则达到概率输出的效果。critic网络输入为state和action，输出为Q值。本文介绍的是off-policy的 Deterministic Actor-Critic，on-policy的结构详见论文。
- DPG：DPG中提供了确定性策略梯度的计算公式和证明。
- DQN：DDPG中借鉴了DQN的experience replay和target network。target network的具体实现与DQN略有不同，DDPG论文中的actor和critic的两个target network以小步长滞后更新，而非隔C步更新。都是为了解决模型训练稳定性问题，大同小异吧。
- Noise sample：连续动作空间的RL学习的一个困难时action的探索。DDPG中通过在action基础上增加Noise方式解决这个问题。
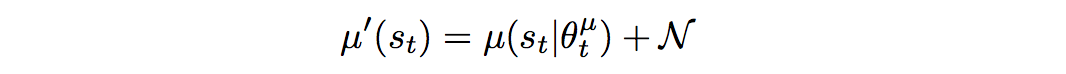
DDPG的算法训练过程：

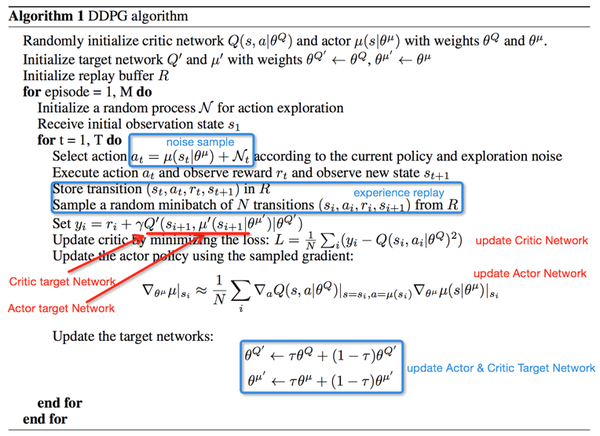
四、some state-of-art papers

写到这整个文章有点太长了，这部分会拆分到后续单独开辟文章介绍。简单介绍下大名鼎鼎的A3C算法。

4.1 Asynchronous Advantage Actor-Critic (A3C)

因为后续还有计划A3C和Advantage结合在一起分享下。这里只是大体理一下A3C的主要思路。
- asynchronous：异步，对应的异步分布式RL框架。相对应的是15年google的Gorila平台Massively Parallel Methods for Deep Reinforcement Learning，Gorilla采用的不同机器，同一个PS。而A3C中，则是同一台机器，多核CPU，降低了参数和梯度的传输成本，论文里验证迭代速度明显更快。并且更为重要的是，它是采用同机多线程的actor-learner对，每个线程对应不同的探索策略，总体上看样本间是低相关的，因此不再需要DQN中引入experience replay机制来进行训练。这样能够采用on-policy的方法进行训练。此外，训练中采用的是CPU而非GPU，原因是RL在训练过程中batch一般很小，GPU在等待新数据时空闲很多。附异步方法抽象的架构图见下：
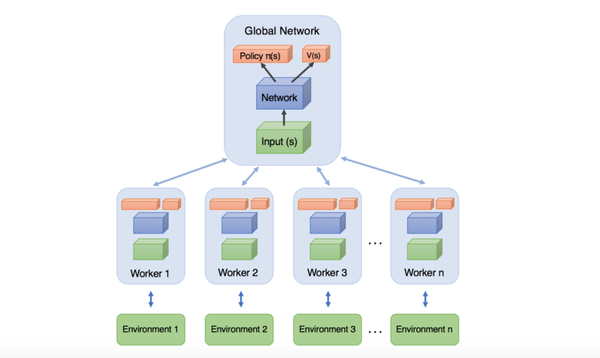
- Advantage Actor-Critic：和DDPG架构类似，actor网络的梯度：
与DDPG不同的是A3C利用的是max(Advantage)而非max(Q)，其中 $A(s_{t},a_{t}; heta , heta _{v})$ 是利用n-steps TD error进行更新的，即：

具体过程见下图：

n-step Q-learning A3C算法训练过程：

4.2 Trust Region Policy Optimization（TRPO）and action embedding and ...

16年Berkeley大学的论文 Trust Region Policy Optimization，核心在于学习的可信度，提高模型稳定性。

超大规模离散动作空间的action embedding的paperDeep Reinforcement Learning in Large Discrete Action Spaces。核心贡献是引入action embedding，具体做法是将离散动作embedding到连续的小空间中，设计很巧妙，读这篇论文前也有类似思路，可以用到搜索推荐这些领域。

其他前沿文章和专题，比如16年NIPS BestPaper Value Iteration Networks（安利下新朋友iker的分享：强化学习系列三- Value iteration Network）以及又是Silver大神16年的Fictitious Self-Play Deep Reinforcement Learning from Self-Play in Imperfect-Information Games等，留待后面文章再仔细分解了。

五、some words

一点点感触，平时很少写文章，平时要学的东西很多项目也很busy，时间真心不多...但写到这里反而发现，能够把学习思考实践的内容通过写作呈现出来，还是有些不同于单独读paper做实验的收获，写作的过程会加深对细节的理解，也能从更系统更全面视角看待问题，后续会继续多po一些前沿专题和实现象，继续保持更新，各位看官多多支持哈。DRL是一个非常有意思的方向，欢迎多多交流指导，DRL领域的发展也是日新月异，生活在这样一个信息革命大变革时代也是我们的幸运。anyway，最重要的是开心，加油吧~

最后安利下我们team的招聘，对淘宝搜索排序感兴趣的同学欢迎邮件我 qingsong.huaqs@taobao.com，来淘宝，一起成长！
相关阅读:
jmeter压测学习42-逻辑控制器之交替控制器
 jmeter压测学习41-逻辑控制器之吞吐量控制器
 jmeter压测学习40-逻辑控制器之事务控制器
 jmeter压测学习39-获取post请求x-www-form-urlencoded格式的数据
 jmeter压测学习38-通过Jython调用Python脚本
 对微信小程序的生命周期进行扩展 – Typescript 篇
 在微信小程序开发中使用Typescript
TCP长连接和短连接 Python代码
 jQuery Ajax编程
 Django 网页中文显示u开头的乱码
原文地址：https://www.cnblogs.com/skykill/p/6786629.html