[题解]洛谷P1350车的放置

题目链接：车的放置

题目描述：

有下面这样的一个网格棋盘，a，b，c，d表示了对应边长度，也就是对应格子数。

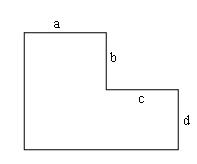
当a=b=c=d=2时，对应下面这样一个棋盘

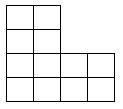
要在这个棋盘上放K个相互不攻击的车，也就是这K个车没有两个车在同一行，也没有两个车在同一列，问有多少种方案。同样只需要输出答案mod 100003后的结果。

 解题思路：

这个图形不太规整，但还是可以dp来写，需要先记录每一列的高度，记为lim【[i]，dp[i][j]表示从后往前到了第i列，选了j个的方案数。对于限制条件，可以从大区间中减去小区间来处理，dp方程：f[i][j]=(f[i-1][j]+((lim[i]-j+1)*f[i-1][j-1])%mod)%mod;

代码：

#include<bits/stdc++.h>
#define ll long long 
#define R register
using namespace std;
const int N=2e3+5;
int a,b,c,d,k,f[N][N],mod=1e5+3,lim[N];//后 i 列, 选了 j 个的 方案数
int main(){
    memset(f,0,sizeof(f));
    scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
    for(R int i=1;i<=c;i++)lim[i]=d,f[i][0]=1;
    for(R int i=c+1;i<=a+c;i++)lim[i]=b+d,f[i][0]=1;
    f[0][0]=1;
    for(R int i=1;i<=a+c;i++)
    for(R int j=1;j<=i;j++)
    f[i][j]=(f[i-1][j]+((lim[i]-j+1)*f[i-1][j-1])%mod)%mod;
    printf("%d",f[a+c][k]);
    // i=     1     ------->     n
    // j=     1     -------->    i;
    //f[i][]]=f[i-1][j]+(lim[i]-j+1)*f[i-1][j-1];
    return 0;
}