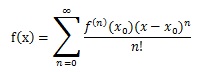
泰勒级数的样式并不难理解，简而言之，就是用一个多项式函数来表达另一个函数，我们需要这样的多项式函数，因为有些函数的处理并不如多项式函数来得方便。我设想了下面的一个构建过程：
以x0为基准点来设计这个函数，我们当然希望新的多项式函数和函数f(x)在x0处所具有的性质保持一致，甚至完全一致。如果f(x)在x0处具有的n阶导数和即将构建的多项式函数相同（也就是说二者函数值的变化趋势相同），那么新函数和f(x)在x0的微小邻域内就会有很好的贴合（尽管并不完全一致），因此构建这样一个函数符合我们的初衷。那么如何让f(x)在x0处具有的n阶导数和即将构建的多项式函数的相应导数相等呢？可以这样想：
1.f(x0)=f(x0)+u(x-x0)我们让多项式中含有f(x0)，剩余的多项式部分u(x-x0)，当x=x0时全部消去。
2.f(x0)=f(x0)+f'(x0)(x-x0)+v(x-x0)我们希望在求一阶导数时等式右边只剩下f'(x0)，再在上式的基础上加入一项f'(x0)(x-x0)，v(x-x0)这一部分同样会消失，常数项f(x0)求导后归为0，f'(x0)(x-x0)求导剩下了f'(x0)。
3.f(x0)=f(x0)+f'(x0)(x-x0)+(f''(x0)(x-x0)2)/2!+g(x-x0)两边求二阶导数，新加入的项(f''(x0)(x-x0)2)/2!求二阶导数后恰好为f''(x0)，g(x-x0)部分因为x取x0而归为0，前两项求导后也消失。
以此类推，往后多做几步规律就出来了，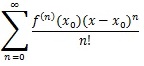
这样一种多项式满足我们最初提出的要求，所以构建泰勒公式的核心便是使多项式中总有一项求n阶导数后恰好对应于f(x)的n阶导，其他项因为是常数项导数为0，或者是求导后含有(x-x0)，在x0处也被消去，最终都消失。
我不确定泰勒当年的心路历程是否如此，幻想一下，如果换作我第一个构建出了这样一种奇妙的式子，肯定会无比兴奋。
说到泰勒级数，也联想到傅里叶级数，以及数列极限，类似的东西在高等数学中经常出现，自己也在总结，无非就是数值表示的无穷形式，与之对应的是有穷形式，最典型的就是有限小数和无限小数，我感觉在本质上这些数都是一致的，没有孰轻孰重之分，他们都是数值，一样的普通，一样的平等，正因为这种一致性，类似泰勒级数这种用无穷形式表示有穷形式才有可能发生，尽管在心里上我们更愿意接受有穷形式，似乎它是确定的，而不大愿意接受无穷形式，好像它是无限的不确定的。其实这种无穷形式的存在，是因为我们预设了前提在里面，所有我们的数学运算都有相同的预设前提，在这个前提下我们所作的一切才有了意义，如果换一种前提，那么可能原先的无理数会变成有限形式，而原先的有理数会变成无理数。类似的例子，比如温度，我们预设的前提就是水沸腾的温度为100度，没有理由，为什么不是50度或者200度？完全是可以的，只有预设前提我们才能量化问题。同样的，数学问题的逻辑推演也是以特定的前提才能进行逻辑推演，再比如，我们用三进制来表示数字，那么现在有限小数统统会变成无限小数，而三分之一本来是无限循环小数，在三进制下却变成了0.1是一个有限小数。看不大出这种的思考有多大意义，聊以自慰，哈哈。。。
