http://blog.csdn.net/xiajun07061225/article/details/7766838
在三维变换中,经常要用到旋转变换,而且很多变换是围绕任意轴的。那么下面就介绍绕任意单位轴旋转的两种方法。
假设要旋转的角度是a,围绕的轴是r。
方法一:
(1)构建新的基
寻找另外两条单位长度的坐标轴s、t,他们相互垂直,而且与r垂直。这样r、s、t组成了一组新基。
具体求s的方法:
找到r中的最小分量,将其设置为0.然后交换其他两个分量,接着将第一个非零的分量取反(实际上也可以对另外一个非零分量取反)。
要求t,只需求r、s的叉积即可。
详细计算公式:

这样就确保了r、s、t组成了一组正交单位基。
(2)将标准基变换到新的基。
需要通过变换使得r和x轴重合,这样之后的旋转就是绕x轴的普通旋转。另外的两个轴也相互重合。
变换矩阵由上面的r、s、t向量组成:

(3)旋转
因为r与x重合,在新的基中我们只需围绕x轴进行旋转(正常情况下的旋转)即可。
假设旋转矩阵是Rx(a)。
(4)变换回到原来的标准基。
变换矩阵应该是M的逆矩阵,由于M是正交的,因此其逆矩阵就是其转置矩阵。
因此,最终的绕任意单位轴的变换矩阵是:

方法二
根据Goldman给出的公式进行计算,这个公式有点复杂:
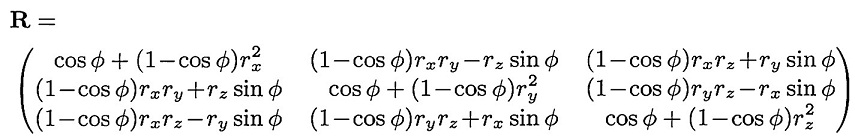
具体推导过程可以参考:
http://www.cppblog.com/lovedday/archive/2008/01/12/41031.html
http://www.cnblogs.com/cg_ghost/archive/2012/04/27/2473347.html
再分享一下我老师大神的人工智能教程吧。零基础!通俗易懂!风趣幽默!还带黄段子!希望你也加入到我们人工智能的队伍中来!https://blog.csdn.net/jiangjunshow