120. Triangle

一、题目

　　1、审题

　　　

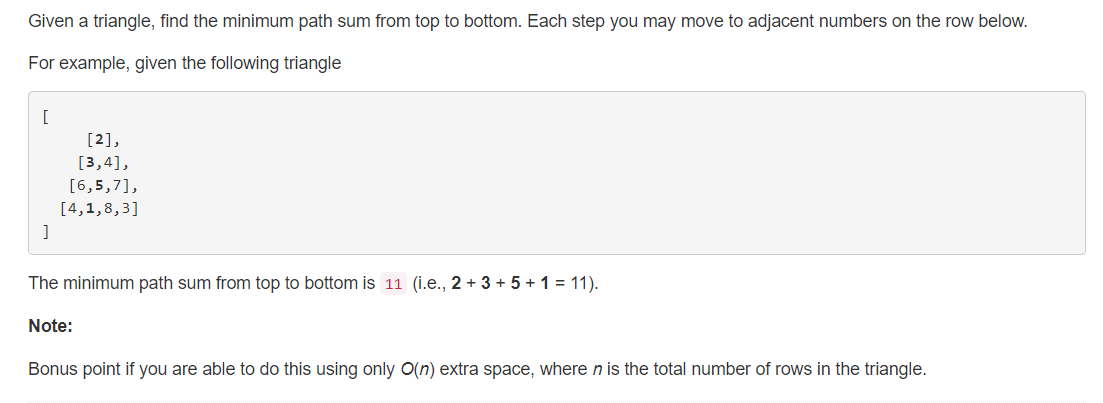
　　2、分析

　　　　给出一个三角形，找出从顶到底端链接的路径和最短的路径和。

 二、解答

　　1、思路：　

　　　　方法一、

　　　　　　采用 DP 方式，顶 ---> 底，确定从顶点到下一行的各个元素的最短路径和，最终返回最后一行的最小值。

    public int minimumTotal2(List<List<Integer>> triangle) {
    
        int n = triangle.size();
        int[][] minLen = new int[n][n];
        minLen[0][0] = triangle.get(0).get(0);
        
        if(n == 1)
            return minLen[0][0];
        
        int minSum = Integer.MAX_VALUE;
        for (int i = 1; i < n; i++) {
            for(int j = 0; j <= i; j++) {
                if(j == 0)
                    minLen[i][j] = triangle.get(i).get(j) + minLen[i-1][j];
                else if(j == i)
                    minLen[i][j] = triangle.get(i).get(j) + minLen[i-1][j-1];
                else 
                    minLen[i][j] = triangle.get(i).get(j) + Math.min(minLen[i-1][j], minLen[i-1][j-1]);
                
                if(i == n - 1 && minSum > minLen[i][j])
                    minSum = minLen[i][j];
            }
        }
        return minSum;
    }

　　方法二、

　　　　采用 DP 方式，底 --> 顶，依次确定从底到此一行的各个元素最短路径和，最终返回 arr[0][0];

   public int minimumTotal(List<List<Integer>> triangle) {
     
        int n = triangle.size();
        int[] minLen = new int[n];
        int index = 0;
        for(Integer i: triangle.get(n-1))
            minLen[index++] = i;
        // bottom --> top
        for(int layer = n - 2; layer >= 0; layer--) { // 从倒数第二行开始
            for(int i = 0; i <= layer; i++) {    // 更新此行的每一个节点
                minLen[i] = Math.min(minLen[i], minLen[i+1]) + triangle.get(layer).get(i); 
            }
        }
        return minLen[0];
    }