一、题目
1、审题
2、分析
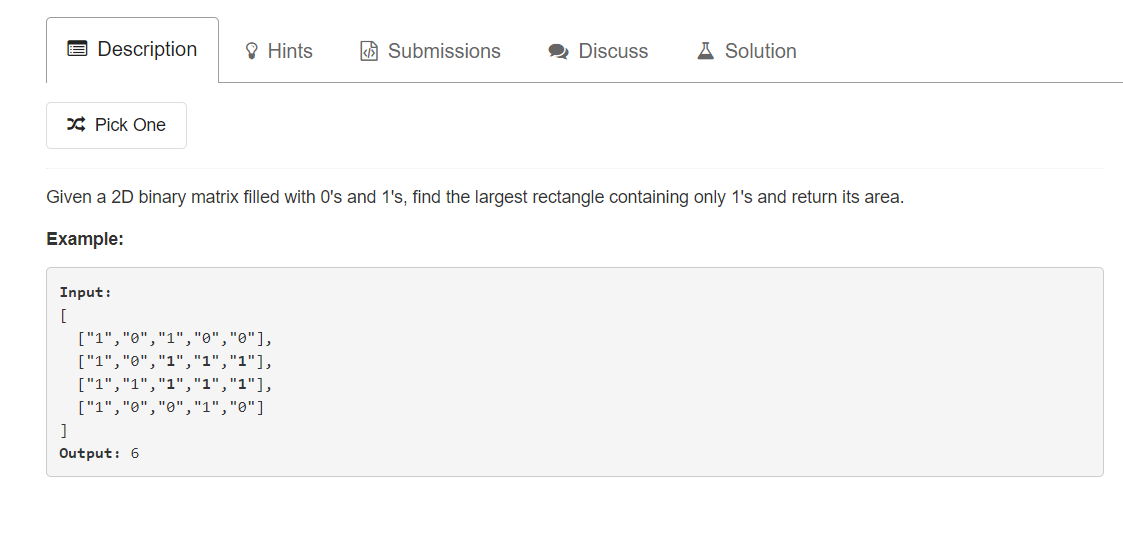
给出一个含有 ‘0‘、’1’ 字符的矩阵,求其中的 ‘1‘ 形成的子矩阵的最大面积。
二、解答
1、思路:
采用三个一维数组:
left[cols]: 若该元素为 ‘1‘,则记录此元素以及之前行的形成矩阵的最大左边界。
right[cols]: 若该元素为 ‘1‘,则记录此元素以及之前行的形成矩阵的最大右边界。
right[cols]: 若该元素为 ‘1‘,则记录此元素以及之前行具有相同左右边界的矩阵的最大高度。
public int maximalRectangle(char[][] matrix) { if (matrix == null || matrix.length == 0 || matrix[0] == null || matrix[0].length == 0) return 0; int m = matrix.length; int n = matrix[0].length; int maxArea = 0; int[] left = new int[n]; int[] right = new int[n]; int[] height = new int[n]; Arrays.fill(right, n-1); for (int i = 0; i < m; i++) { // 每一行 int rB = n - 1; for(int j = n - 1; j >= 0; j--) { // 填充 right[j] if(matrix[i][j] == '1') { right[j] = Math.min(right[j], rB); // 考虑上面行的 右边界 } else { right[j] = n - 1; // 代表此元素为 0 rB = j - 1; // 假想下一个元素右边为 1 的边界 } } int lB = 0; for (int j = 0; j < n; j++) { if(matrix[i][j] == '1') { left[j] = Math.max(left[j], lB); // 考虑上面行的左边界 height[j]++; maxArea = Math.max(maxArea, height[j] * (right[j] - left[j] + 1)); } else { height[j] = 0; // left[j] = 0; // 代表此元素为 0 lB = j + 1; // 假想下一个元素的左边为 1 的边界 } } } return maxArea; }