一、题目
1、审题
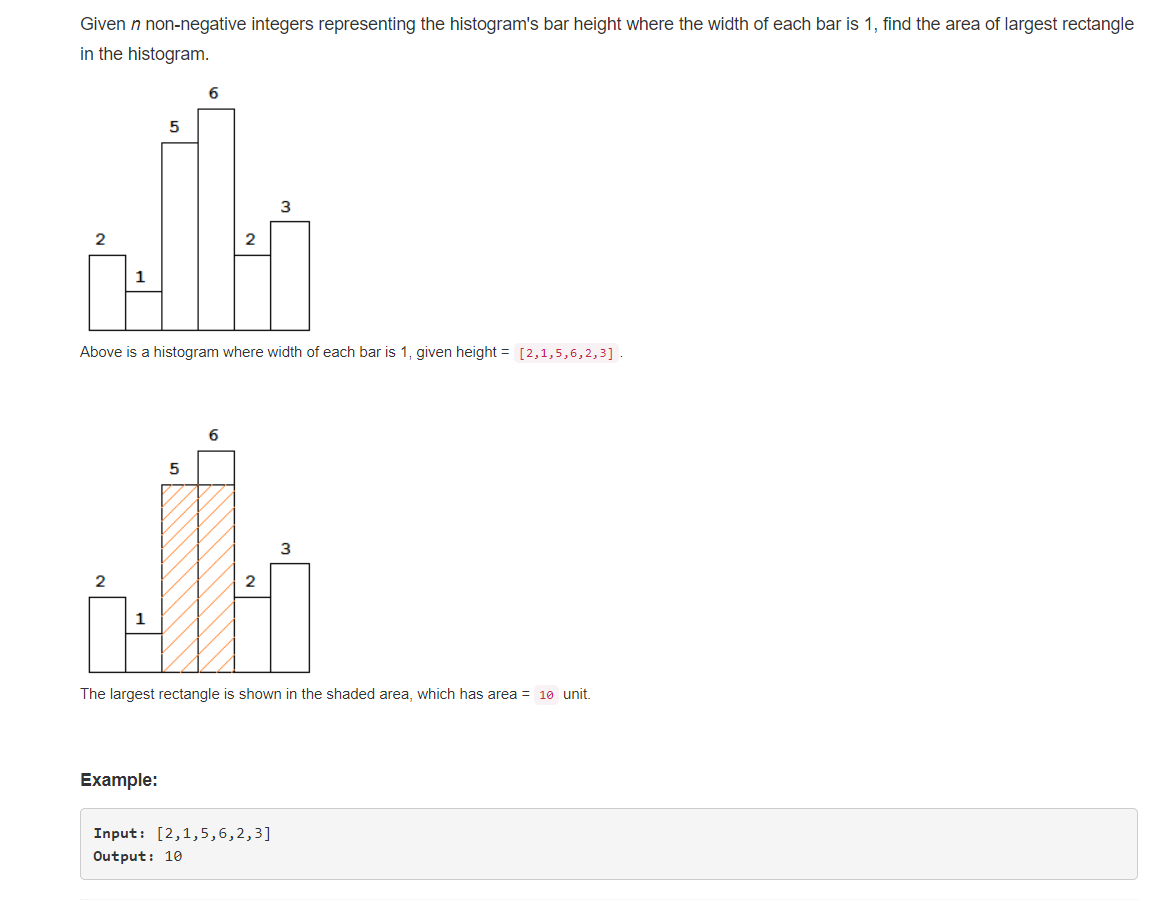
2、分析
给一个正整数数组代表高度,且宽度为1,求该数组形成的矩形所能存储的最大容量。
二、解答
1、思路:
方法一:
列举出数组形成的矩形,即可找到最大容量。
即宽度为 1 、2、3......n 的矩形, 其中高度为连续的 i 个整数中最小的一个。
注意(使用 3 层循环,时间超出)
public int largestRectangleArea(int[] heights) { int len = heights.length; if(len == 0) return 0; int max = 0; for (int i = 1; i <= len; i++) { // 几个数之和 for (int j = 0; j <= len - i; j++) { // 计算连续 i 个数之和 if(i == 1) { max = Math.max(max, heights[j]); } else { int min = heights[j]; for (int k = j; k < j+i; k++) { if(heights[k] < min) min = heights[k]; } max = Math.max(max, min * i); } } } return max; }
方法二、使用一个栈进行记录。
根据元素的升序将数组分成 n 份,栈中每次处理 1 份,且处理时若第 i+1 份的最小值大于第 i 份的某个值,则该值是继续保持在栈中的。
栈的特征为:
①、栈中存放的下标的元素是升序的
②、每个 index 均入栈
③、栈为空,则表示下标 i 的前边的元素值均比下标 i 的元素大
④、 i - 1 - stack.peek() 表示的是以该元素值为高时,所形成的矩阵的最大宽度。
public int largestRectangleArea3(int[] heights) { int len = heights.length; Stack<Integer> stack = new Stack<>(); int maxArea = 0; for (int i = 0; i <= len; i++) { int cur = (i == len ? -1 : heights[i]); while(!stack.isEmpty() && heights[stack.peek()] >= cur) { int h = heights[stack.pop()]; int w = stack.isEmpty() ? i : i - 1 - stack.peek(); maxArea = Math.max(maxArea, h*w); } stack.push(i); } return maxArea; }