一、题目
1、审题
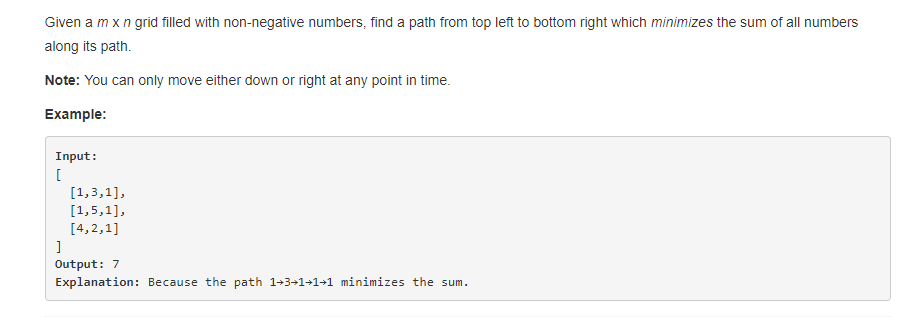
2、分析
给出一个 mXn 方格,求从左上角到右下角经过的路线中数值和最小的那条路径的路径和。(只能向右、向下移动)
二、解答
1、思路:
方法一、
新建一个一维数组 dp 用于记录到达此格点的最小路径和。遍历所给二维数组 grid:
①、当遍历的是第一行时, dp[i] = grid[0][i] + grid[0][i-1];代表路径和为此格点数值加上左一个节点的路径之和。
②、当遍历的不是第一行时, dp[i] = grid[j][i] + Math.min(dp[i-1], dp[i]); 其中 Math.min(dp[i-1], dp[i]) 中的 dp[i-1] 代表左一格点的距离,dp[i] 代表上一格点的距离。
class Solution { public int minPathSum(int[][] grid) { int row = grid.length; int column = grid[0].length; int[] dp = new int[column]; dp[0] = grid[0][0]; // 迭代从第二行开始 for(int j = 0; j < row; j++) { for (int i = 0; i < column; i++) { if(j == 0) { // 初始化第一行 if(i != 0) dp[i] = dp[i-1] + grid[0][i]; } else { if(i != 0) dp[i] = grid[j][i] + Math.min(dp[i-1], dp[i]); else // 第一行 dp[i] += grid[j][i]; } } } return dp[column-1]; } }
方法二、
不使用额外数组,直接修改 grid 为表示每一个格点距离的数组。
①、初始化 grid 第一行、第一列为距离
②、迭代初始化 grid 所有数值.
public int minPathSum(int[][] grid) { int m = grid.length; int n = grid[0].length; // 初始化第一行的距离 for (int i = 1; i < m; i++) { grid[i][0] += grid[i-1][0]; } // 初始化第一列的距离 for(int i = 1; i < n; i++) grid[0][i] += grid[0][i-1]; for (int i = 1; i < m; i++) { for (int j = 1; j < n; j++) { grid[i][j] += Math.min(grid[i-1][j], grid[i][j-1]); } } return grid[m-1][n-1]; }