一、题目
1、审题
2、分析:
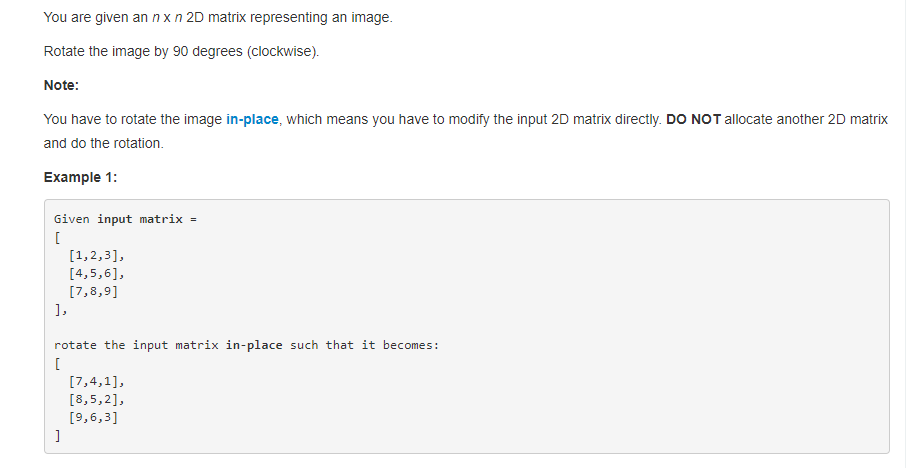
给出一个二维数组代表的矩阵,求得矩阵顺时针旋转90度后的新矩阵。
二、解答
1、思路:
方法一、观察可知,原矩阵与新矩阵的对应关系如下:
①、原矩阵的列 == 新矩阵的行;
②、原矩阵的行 + 新矩阵的列 == 矩阵的最大行号
故借助一个二维数组可以实现
class Solution { public void rotate(int[][] matrix) { int maxIndex = matrix.length-1; int[][] newMatrix = new int[maxIndex+1][maxIndex+1]; for (int i = 0; i <= maxIndex; i++) { for (int j = 0; j <= maxIndex; j++) { newMatrix[j][maxIndex - i] = matrix[i][j]; } } for (int i = 0; i < newMatrix.length; i++) { for (int j = 0; j < newMatrix.length; j++) { matrix[i][j] = newMatrix[i][j]; } } } }
方法二、不申请新数组,直接在原数组的基础上进行交换。

①、顺时针交换:
a、将二维数组列元素进行旋转;
b、将二维数组对称元素进行交换。
②、逆时针旋转:
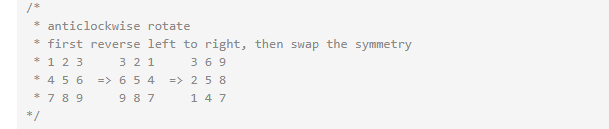
a、将行元素进行旋转;
b、将二维数组对称元素进行交换。
public void rotate(int[][] matrix) { int len = matrix.length; for (int i = 0, j = len - 1; i < j; i++, j--) { for (int k = 0; k < len; k++) { int tmp = matrix[i][k]; matrix[i][k] = matrix[j][k]; matrix[j][k] = tmp; } } for (int i = 0; i < len; i++) { for (int j = i+1; j < len; j++) { // 注意: j = i + 1 开始; int tmp = matrix[i][j]; matrix[i][j] = matrix[j][i]; matrix[j][i] = tmp; } } }