[OI学习笔记]树状数组

背景

　　花了一个上午，终于把树状数组弄懂了。。。

　　打了三种树状数组的模板：树状数组单点更新区间查询，线段树区间更新单点查询，树状数组区间更新区间查询。

　　第三种太毒了，，，好久才明白

 树状数组

　　就是树一样的数组，它的底层实现其实就是一个数组，但是我们把它yy成了一棵树。。。

　　

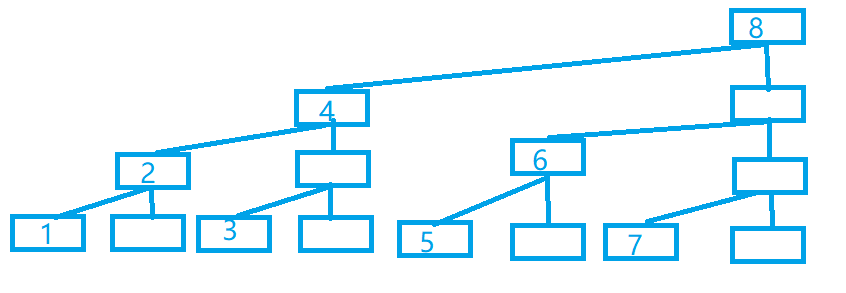
　　他的每一列的最顶端有一个元素，而其他位置都是我们yy出来的，他在程序中并不会出现，每一个非叶子节点都是他两个子节点储存信息的综合（可以是和，乘积或最大值等等）。

　　树状数组用来求前缀和，如果你想求任意的区间和则用两个前缀和只差即可

lowbit操作

　　lowbit[i]定义为：点i所“支配”的叶子节点的个数

　　怎么理解呢？比如说：上图中lowbit[2]=2,lowbit[4]=4,lowbit[7]=1（叶子节点算1）

　　然后，我们惊人地发现：一个点的父节点和这个点的横向距离，一个点和他左边那个区间节点的横向距离，都是这个节点的lowbit！

　　这样，我们就可以用lowbit很方便地从一个区间转移到另一个包含它的区间了！

　　举个栗子：

　　第一种：从1依次转移到2,4,8：

　　

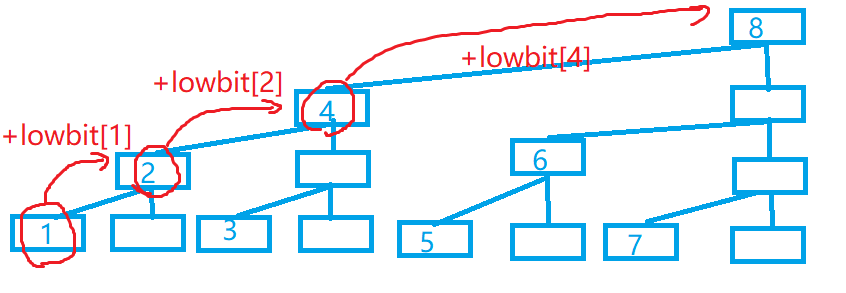
　　第二种：从7依次转移到6,4：

　　

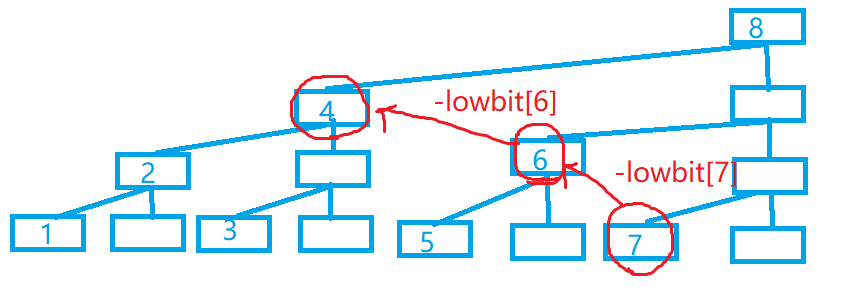
　　向右转移：在刚才第一种转移的过程中，我们可以完成用子节点更新父节点的值（刚才更新了1,2,4,8）

　　向左转移：而在第二种转移中，可以完成对一段前缀和的统计（刚才统计的区间[1,7]）

　　那么，lowbit[i]怎么求呢？这里直接写一个结论：

　　　　　　　　　　lowbit[i]=i&(-i)

单点更新区间查询

　　这个比较简单，按照上面的方法结合lowbit公式一步一步转移即可

　　代码：

#include<cstdio>
#define lowbit(x) (x&(-x))
using namespace std;
const int MAXN=10010;

int c[MAXN],n,m;

void change(int x,int num){
    for(int i=x;i<=n;i+=lowbit(i)){
        c[i]+=num;
    }
}

int ask(int x){
    if(x==0)return 0;//这个不最好加上
    int s=0;
    for(int i=x;i>0;i-=lowbit(i)){
        s+=c[i];
    }
    return s;
}

int main(){
    scanf("%d%d",&n,&m);
    int temp;
    for(int i=1;i<=n;i++){
        scanf("%d",&temp);
        change(i,temp);
    }
    for(int i=1;i<=m;i++){
        int ques;
        scanf("%d",&ques);
        if(ques){
            int x,num;
            scanf("%d%d",&x,&num);
            change(x,num);
        }
        else{
            int left,right;
            scanf("%d%d",&left,&right);
            int s1=ask(right),s2=ask(left-1);
            printf("%d
",s1-s2);
        }
    }
    return 0;
} 

区间更新单点查询

　　区间更新这要记住：原序列用普通数组a存起，更新区间时跑向左转移，标记更新的数值（比如说加多少，乘多少，变成多少等等）

　　（刚刚更改的范围是一个[1,y]，如果你要更改[x,y]别忘记把前面不要的[1,x-1]部分减回来！！！）

　　然后查询点时只要向右转移，按照刚刚打的标记更改即可。（是不是和线段树的lazytag有点像呢）

　　以下是代码：

#include<cstdio>
#define lowbit(x) (x&(-x)) 
using namespace std;
const int MAXN=10010;

int a[MAXN],n,m,c[MAXN];

void change(int x,int num){
    for(int i=x;i>0;i-=lowbit(i)){
        c[i]+=num;
    }
}

int ask(int x){
    int rxz=0;
    for(int i=x;i<=n;i+=lowbit(i)){
        rxz+=c[i];
    }
    return rxz+a[x];
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
    }
    for(int i=1;i<=m;i++){
        int ques;
        scanf("%d",&ques);
        if(ques){
            int left,right,num;
            scanf("%d%d%d",&left,&right,&num);
            change(right,num);
            change(left-1,-num);
        } 
        else{
            int x;
            scanf("%d",&x);
            printf("%d
",ask(x));
        }
    }
    return 0; 
} 

区间更新区间查询

　　这个有点难想。

　　我们考虑原数列a的差分数组c

　　

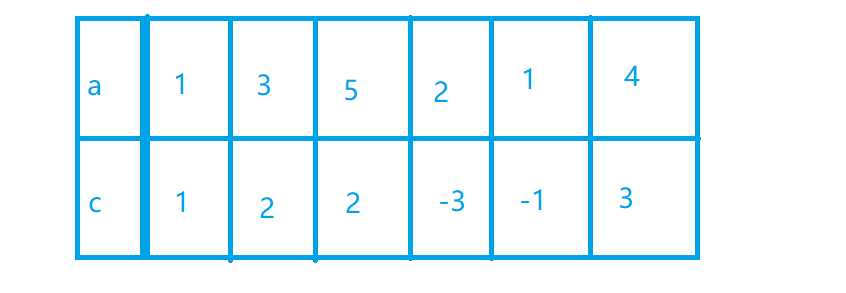
　　差分数组有一个性质：差分数组跑一遍前缀和，得到原数组。

　　可以得到：

　　

　　这样，岂不是可以用差分数组c[i]来表示a[i]?

　　我们只要用一个额外的数组来存储就行了.

　　编程时要注意初始化

　　代码：（d数组为储存的数组）

#include<cstdio>
#define lowbit(x) x&(-x)
using namespace std;
const int MAXN=10010;

int n,m,a[MAXN];
int c[MAXN],d[MAXN];//差分数组&数组d[i]=(i-1)c[i];

void changesection(int x,int num){
    for(int i=x;i<=n;i+=lowbit(i)){
        c[i]+=num;
        d[i]+=(x-1)*num;
    }
}

int asksection(int x){//询问[1,x]前缀和 
    int s=0;
    for(int i=x;i>0;i-=lowbit(i)){
        s+=x*c[i]-d[i];
    }
    return s;
}

int main(){
    //freopen("in.in","r",stdin);
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    //要初始化！！！
    for(int i=1;i<=n;i++)
        changesection(i,a[i]-a[i-1]);
    int ques;
    for(int i=1;i<=m;i++){
        scanf("%d",&ques);
        if(ques){//change section
            int left,right,num;//区间[left,right]，增量num 
            scanf("%d%d%d",&left,&right,&num);
            changesection(left,num);
            changesection(right+1,-num);
        }
        else{//ask section
            int left,right;
            scanf("%d%d",&left,&right);
            int s1=asksection(right),s2=asksection(left-1);
            printf("%d
",s1-s2);
        }
    }
    return 0;
}